The Iwahori-Hecke algebra plays a crucial role in representation theory and algebraic combinatorics, generalizing the group algebra of a Coxeter group with deformation parameters. Its structure influences the study of quantum groups and modular representations, connecting deep aspects of geometry and number theory. Explore the rest of this article to understand how this algebraic framework can impact your research or studies.
Table of Comparison
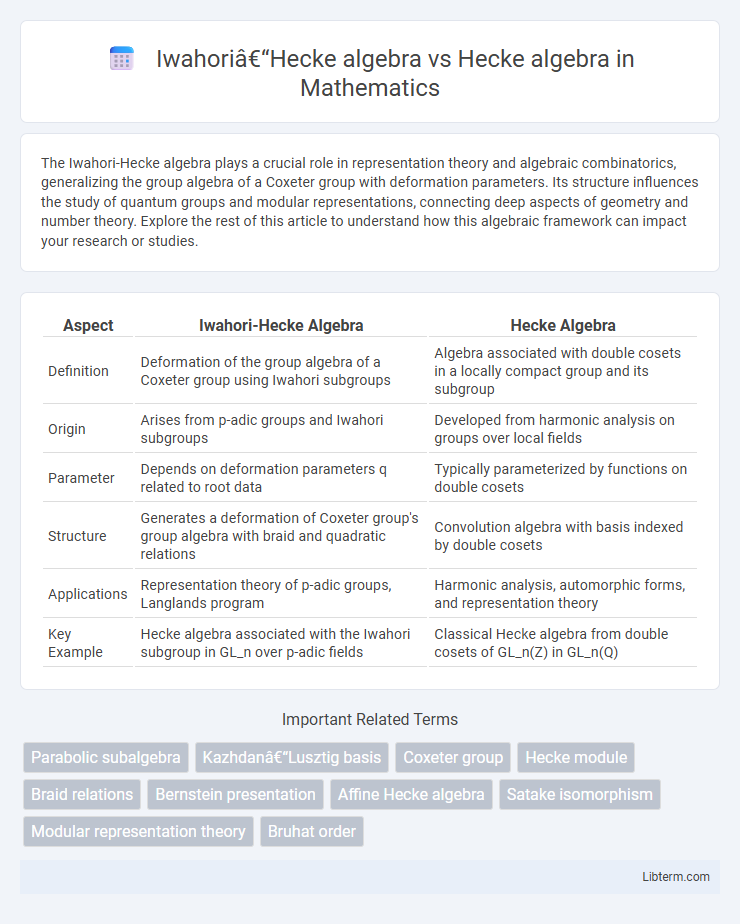
| Aspect | Iwahori-Hecke Algebra | Hecke Algebra |
|---|---|---|
| Definition | Deformation of the group algebra of a Coxeter group using Iwahori subgroups | Algebra associated with double cosets in a locally compact group and its subgroup |
| Origin | Arises from p-adic groups and Iwahori subgroups | Developed from harmonic analysis on groups over local fields |
| Parameter | Depends on deformation parameters q related to root data | Typically parameterized by functions on double cosets |
| Structure | Generates a deformation of Coxeter group's group algebra with braid and quadratic relations | Convolution algebra with basis indexed by double cosets |
| Applications | Representation theory of p-adic groups, Langlands program | Harmonic analysis, automorphic forms, and representation theory |
| Key Example | Hecke algebra associated with the Iwahori subgroup in GL_n over p-adic fields | Classical Hecke algebra from double cosets of GL_n(Z) in GL_n(Q) |
Introduction to Hecke Algebras
Hecke algebras, fundamental in representation theory, arise from Coxeter groups and their associated braid groups, providing algebraic structures that generalize group algebras. The Iwahori-Hecke algebra is a deformation of the group algebra of a Coxeter group parameterized by q, playing a critical role in studying p-adic groups and modular representations. Both algebras capture symmetries encoded by reflections and have applications in number theory, combinatorics, and algebraic geometry.
Defining Iwahori–Hecke Algebras
Iwahori-Hecke algebras generalize Hecke algebras by incorporating a deformation parameter q related to a Coxeter group W, defined over a ring with parameters corresponding to the Iwahori subgroup of a p-adic group. The defining relations of Iwahori-Hecke algebras modify the standard Coxeter group relations by replacing reflections with generators T_s satisfying quadratic relations (T_s - q)(T_s + 1) = 0, encoding both group symmetries and Hecke operators. This construction is fundamental in representation theory, linking the algebraic structure to the geometry of flag varieties and p-adic groups, differentiating it from classical Hecke algebras defined via double coset spaces.
Historical Context and Development
The Iwahori-Hecke algebra originated in the 1960s from the work of Nagayoshi Iwahori and Erich Hecke, building upon the classical Hecke algebras developed earlier in the 1930s to study modular forms and number theory. While classical Hecke algebras are related to double cosets in arithmetic groups, the Iwahori-Hecke algebra generalizes these concepts to affine Weyl groups and plays a crucial role in the representation theory of p-adic groups. This development connected deep algebraic structures with geometric and combinatorial aspects, profoundly influencing the study of quantum groups and Lie theory.
Key Structural Differences
Iwahori-Hecke algebras are deformations of group algebras associated with Coxeter groups, incorporating parameters that adjust the relations defined by the group's braid relations and quadratic relations. In contrast, classical Hecke algebras typically arise from double coset algebras linked to p-adic groups and are often defined without deformation parameters or with simpler parameter structures. The key structural difference lies in the Iwahori-Hecke algebra's explicit dependence on deformation parameters that modify the algebra's basis and representation theory, providing richer geometric and combinatorial interpretations compared to the more rigid structure of traditional Hecke algebras.
Representation Theory Comparison
Iwahori-Hecke algebras generalize Hecke algebras by introducing deformation parameters related to Coxeter groups, which provides richer structures in their representation theory. Representations of Iwahori-Hecke algebras allow categorification and connections to quantum groups, while Hecke algebras primarily capture symmetries of finite groups of Lie type. The study of Iwahori-Hecke algebras reveals deeper insights into modular representation theory and Kazhdan-Lusztig theory compared to classical Hecke algebras.
Root Systems and Generation
Iwahori-Hecke algebras are deformations of the group algebra of Coxeter groups associated with root systems, generated by elements corresponding to simple reflections with parameters encoding root data. Hecke algebras arise from double coset constructions in algebraic groups over finite fields, related to Weyl group symmetries of root systems but typically with a fixed set of generators tied to the underlying root system's simple roots. The generators of Iwahori-Hecke algebras depend on deformation parameters reflecting the structure of affine root systems, while classical Hecke algebras focus on finite root systems and their corresponding Weyl groups.
Applications in Number Theory
Iwahori-Hecke algebras generalize Hecke algebras by incorporating parameters that deform group relations, providing powerful tools in the representation theory of p-adic groups and affine Weyl groups. In number theory, Iwahori-Hecke algebras facilitate the study of modular forms and automorphic representations, particularly through the analysis of local factors and the structure of parahoric subgroups. Hecke algebras, simpler in structure, primarily contribute to understanding classical modular forms and Hecke operators acting on spaces of cusp forms, linking them to L-functions and arithmetic properties of number fields.
Connections to Coxeter Groups
The Iwahori-Hecke algebra is a deformation of the group algebra of a Coxeter group, preserving key structural properties tied to the Coxeter system's generators and relations. Hecke algebras arise naturally in the representation theory of Coxeter groups and play a crucial role in categorifying their combinatorial structures, such as Kazhdan-Lusztig polynomials. Both algebras encode reflection symmetries inherent in Coxeter groups, but the Iwahori-Hecke algebra introduces parameter-dependent relations that generalize classical Hecke algebra constructions linked to finite groups of Lie type.
Categorification and Modern Research
Iwahori-Hecke algebras generalize classical Hecke algebras by incorporating parameters related to reflection groups, playing a central role in the categorification of quantum groups and braid group actions. Modern research explores their connection to categorified knot invariants, such as Khovanov-Rozansky homology, and their applications in higher representation theory, particularly through diagrammatic and 2-representation frameworks. Advances in categorification of Iwahori-Hecke algebras have deepened understanding of geometric representation theory and modular representation theory of finite groups of Lie type.
Future Directions and Open Problems
Future directions in studying Iwahori-Hecke algebras involve exploring their connections to categorification and quantum groups, enhancing understanding of knot invariants and topological quantum field theories. Open problems include classifying module categories over these algebras and determining explicit structures of their centers in non-semisimple cases. Advances in computational approaches to Hecke algebra representations could unlock deeper insights into affine Hecke algebra generalizations and applications in geometric representation theory.
Iwahori–Hecke algebra Infographic
 libterm.com
libterm.com