A symmetric spectrum occurs when the frequency components of a signal are mirrored evenly around a central frequency, often zero in baseband signals. This property simplifies signal analysis and processing, especially in applications like Fourier transforms and communications. Explore the rest of the article to understand how a symmetric spectrum impacts your signal processing tasks.
Table of Comparison
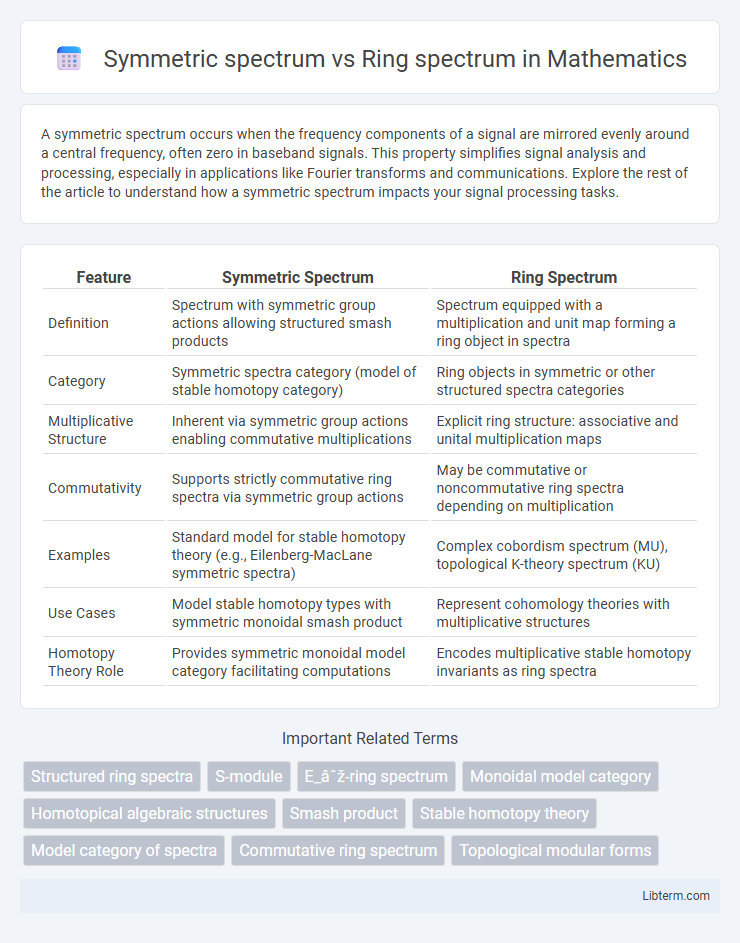
| Feature | Symmetric Spectrum | Ring Spectrum |
|---|---|---|
| Definition | Spectrum with symmetric group actions allowing structured smash products | Spectrum equipped with a multiplication and unit map forming a ring object in spectra |
| Category | Symmetric spectra category (model of stable homotopy category) | Ring objects in symmetric or other structured spectra categories |
| Multiplicative Structure | Inherent via symmetric group actions enabling commutative multiplications | Explicit ring structure: associative and unital multiplication maps |
| Commutativity | Supports strictly commutative ring spectra via symmetric group actions | May be commutative or noncommutative ring spectra depending on multiplication |
| Examples | Standard model for stable homotopy theory (e.g., Eilenberg-MacLane symmetric spectra) | Complex cobordism spectrum (MU), topological K-theory spectrum (KU) |
| Use Cases | Model stable homotopy types with symmetric monoidal smash product | Represent cohomology theories with multiplicative structures |
| Homotopy Theory Role | Provides symmetric monoidal model category facilitating computations | Encodes multiplicative stable homotopy invariants as ring spectra |
Introduction to Spectra in Algebraic Topology
Symmetric spectra and ring spectra are fundamental concepts in algebraic topology used to study stable homotopy theory, providing structured models for spectra that enable rigorous handling of smash products and multiplicative structures. Symmetric spectra incorporate symmetric group actions to facilitate homotopy-theoretic operations, whereas ring spectra are spectra equipped with multiplication and unit maps satisfying associativity and unity up to homotopy, forming the algebraic analog of rings in stable homotopy categories. Understanding the interplay between these spectra is essential for constructing and analyzing generalized cohomology theories and their multiplicative properties.
Defining Symmetric Spectra
Symmetric spectra are structured collections of pointed spaces indexed by natural numbers, equipped with actions of symmetric groups that encode permutation symmetries, enabling a well-behaved smash product and stable homotopy category. Ring spectra are symmetric spectra with a multiplicative structure given by a unital and associative product map, allowing them to serve as generalized ring objects in stable homotopy theory. The enhanced symmetry in symmetric spectra supports the construction of highly structured ring spectra facilitating advanced computations in algebraic topology.
Understanding Ring Spectra
Ring spectra are structured objects in stable homotopy theory equipped with a multiplication that is associative and unital up to homotopy, enabling the study of algebraic structures on spectra. Unlike symmetric spectra, which emphasize strict symmetric monoidal structures, ring spectra focus on encoding multiplication laws that allow for operadic or monoidal interpretations essential in modern homotopy theory and derived algebraic geometry. Understanding ring spectra involves analyzing their role as homotopical analogs of rings, crucial for defining cohomology theories with multiplicative structures and formulating generalized algebraic operations in a topological context.
Structural Differences Between Symmetric and Ring Spectra
Symmetric spectra feature a sequence of pointed spaces with actions by symmetric groups, allowing for symmetric monoidal smash products to form strict commutative ring spectra. Ring spectra, defined within operadic or monoidal contexts, emphasize multiplication maps satisfying associativity and unital conditions but may lack the strict symmetric group actions present in symmetric spectra. These structural differences impact how homotopy-theoretic multiplications and commutative structures are modeled, with symmetric spectra providing a more algebraically rigid framework compared to traditional ring spectra constructions.
Homotopy Theory and Model Categories
Symmetric spectra and ring spectra serve as foundational structures in stable homotopy theory, with symmetric spectra providing a robust model category framework that supports homotopy-invariant symmetric monoidal products. Ring spectra, as monoids in symmetric spectra categories, enable structured multiplicative operations essential for developing highly structured ring objects in stable homotopy categories. Model category techniques applied to symmetric spectra facilitate the construction of homotopically meaningful ring spectra, crucial for computations in algebraic topology and derived algebraic geometry.
Examples of Symmetric and Ring Spectra
Examples of symmetric spectra include the suspension spectrum of a pointed space and the Eilenberg-MacLane spectrum representing ordinary cohomology, both constructed with symmetric group actions enabling stable homotopy computations. Ring spectra examples consist of the sphere spectrum, serving as the unit for the smash product, and the complex cobordism spectrum MU, which carries a highly structured multiplication making it a central object in stable homotopy theory. These spectra play crucial roles in algebraic topology by providing frameworks for generalized cohomology theories and structured ring-like operations.
Multiplicative Structures and Monoidal Properties
Symmetric spectra possess a strictly associative and commutative smash product, making them ideal for modeling highly structured ring spectra with well-behaved multiplicative structures in stable homotopy theory. Ring spectra, defined as monoids in the category of spectra, benefit from symmetric spectra's monoidal closed structure, ensuring coherence and stronger control over module categories and homotopical algebra. The symmetric monoidal structure of symmetric spectra contrasts with the less rigid monoidal properties of classical ring spectra, facilitating advanced constructions like structured ring and module spectra.
Applications in Stable Homotopy Theory
Symmetric spectra provide a structured category enabling convenient model category structures that simplify the construction and manipulation of ring spectra in stable homotopy theory. Ring spectra, viewed as monoids in symmetric spectra, play a crucial role in representing generalized cohomology theories and facilitating multiplicative structures in homotopy categories. The interplay between symmetric and ring spectra advances computations in stable homotopy groups and supports the formulation of higher algebraic structures such as E-infinity ring spectra.
Advantages and Limitations of Each Spectrum
Symmetric spectra provide a well-structured model for stable homotopy theory with better categorical properties, such as strict symmetric monoidal structure and improved handling of smash products, which simplifies constructions and computations. Ring spectra, on the other hand, offer an algebraic framework capturing multiplicative structures essential for performing homotopy-theoretic algebra but may lack the strict commutativity and coherence found in symmetric spectra, sometimes complicating their manipulation. The limitation of symmetric spectra lies in their complexity and technical overhead for explicit constructions, whereas ring spectra might face challenges related to weaker coherence conditions and less rigid multiplicative frameworks.
Conclusion: Choosing Between Symmetric and Ring Spectra
Choosing between symmetric spectra and ring spectra depends on the specific mathematical framework and computational goals; symmetric spectra offer more straightforward symmetric monoidal structures ideal for stable homotopy theory computations, while ring spectra provide a richer algebraic structure essential for studying multiplicative cohomology theories. Ring spectra facilitate intricate operations and module theories that extend beyond the capabilities of symmetric spectra, making them preferable in advanced algebraic topology contexts. Researchers must weigh computational efficiency against algebraic complexity to select the appropriate spectrum type for their homotopical and categorical objectives.
Symmetric spectrum Infographic
 libterm.com
libterm.com