Free modules are algebraic structures with a basis that enables every element to be uniquely represented as a linear combination of basis elements, providing a straightforward way to understand module properties. Injective modules, on the other hand, are characterized by their ability to extend homomorphisms from submodules to the entire module, playing a crucial role in module theory and homological algebra. Explore the rest of this article to deepen your understanding of how free and injective modules function and interact in various algebraic contexts.
Table of Comparison
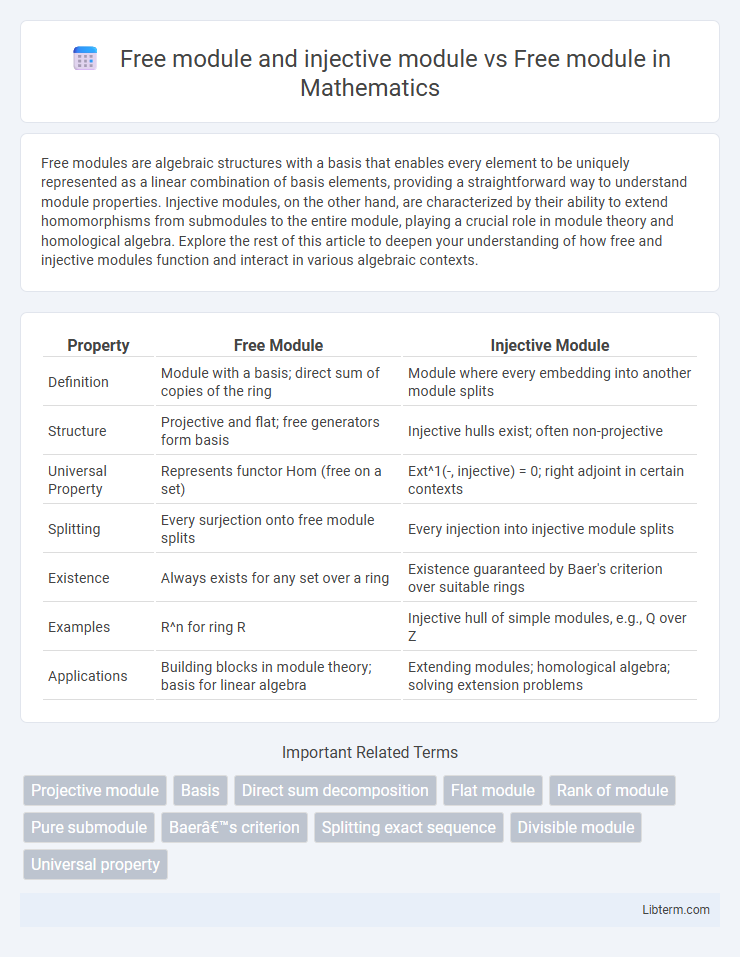
| Property | Free Module | Injective Module |
|---|---|---|
| Definition | Module with a basis; direct sum of copies of the ring | Module where every embedding into another module splits |
| Structure | Projective and flat; free generators form basis | Injective hulls exist; often non-projective |
| Universal Property | Represents functor Hom (free on a set) | Ext^1(-, injective) = 0; right adjoint in certain contexts |
| Splitting | Every surjection onto free module splits | Every injection into injective module splits |
| Existence | Always exists for any set over a ring | Existence guaranteed by Baer's criterion over suitable rings |
| Examples | R^n for ring R | Injective hull of simple modules, e.g., Q over Z |
| Applications | Building blocks in module theory; basis for linear algebra | Extending modules; homological algebra; solving extension problems |
Introduction to Modules in Algebra
Free modules, characterized by having a basis allowing unique linear combinations, serve as a fundamental concept in module theory, similar to vector spaces over a field. Injective modules, defined by their property that every module homomorphism from a submodule extends to the entire module, contrast with free modules as they need not have a basis or be projective. Understanding these differences is crucial for exploring module decompositions and exact sequences in algebra.
Overview of Free Modules
Free modules are algebraic structures characterized by having a basis, allowing every element to be uniquely expressed as a linear combination of basis elements over a ring. Unlike injective modules, which satisfy an extension property and are essential in homological algebra, free modules provide a straightforward generalization of vector spaces to arbitrary rings. The canonical example of a free module is the direct sum of copies of the ring itself, capturing the essence of linear independence and generating sets in module theory.
Defining Injective Modules
Injective modules are defined as modules that satisfy the extension property for module homomorphisms, meaning every homomorphism from a submodule to an injective module can be extended to the entire module. Unlike free modules, which have a basis and are projective by nature, injective modules are characterized by their ability to absorb extensions, making them essential in homological algebra. This distinction highlights injective modules' role in resolving exact sequences and provides a dual perspective to the structural simplicity of free modules.
Key Properties of Free Modules
Free modules over a ring R are characterized by having a basis, meaning every element can be uniquely expressed as a linear combination of basis elements, which ensures projectivity and exactness in sequences. Injective modules, in contrast, are defined by their capacity to extend homomorphisms, often lacking a readily describable basis and thus not necessarily free or projective. Key properties of free modules include their role as direct sums of copies of R, making them flat and projective, whereas injective modules serve as essential extensions that preserve exactness from the opposite perspective.
Essential Characteristics of Injective Modules
Injective modules are characterized by their ability to extend module homomorphisms from submodules to the entire module, making them essential in solving extension problems in module theory. Unlike free modules, which are built from direct sums of copies of the ring and provide a basis for module construction, injective modules possess the property of being direct summands of any module containing them as a submodule, ensuring maximality in terms of homomorphism extension. This essential extensibility property distinguishes injective modules from free modules, emphasizing their role in homological algebra and module decomposition.
Free Module vs Injective Module: Main Differences
Free modules are direct sums of copies of the ring and provide a basis that allows unique linear combinations, whereas injective modules serve as essential extensions where every module homomorphism can be extended. A key difference lies in their structural roles: free modules are projective and characterized by their basis, while injective modules possess an extension property that makes them critical in homological algebra and exact sequences. Free modules are often easier to construct explicitly, whereas injective modules are typically used to resolve modules and study module decompositions via injective envelopes.
Applications of Free Modules in Algebra
Free modules serve as fundamental building blocks in algebra, facilitating the study of module homomorphisms and exact sequences due to their basis structure and projective properties. Unlike injective modules, which are primarily used to analyze extensions and cohomological dimensions, free modules simplify constructions in linear algebra over rings, particularly in module decomposition and classification problems. Applications include encoding solutions to linear equations over rings, enabling explicit computation in homological algebra, and providing a framework for understanding projective modules and flatness in commutative algebra.
Applications of Injective Modules in Algebra
Injective modules play a crucial role in homological algebra and module theory due to their property of extending module homomorphisms, which aids in constructing injective resolutions essential for computing derived functors like Ext and Tor. Unlike free modules that have a basis and facilitate straightforward structural analysis, injective modules offer powerful tools for addressing extension problems and decomposing modules in exact sequences. Applications of injective modules include simplifying cohomology computations, analyzing local cohomology in commutative algebra, and resolving modules over rings with certain finiteness conditions.
Examples Illustrating Free and Injective Modules
Free modules, such as the module \(\mathbb{Z}^n\) over the ring \(\mathbb{Z}\), have a basis allowing unique linear combinations for every element, exemplifying their structure and simplicity. Injective modules like the \(\mathbb{Q}\) module over \(\mathbb{Z}\) serve as divisible abelian groups where any extension problem can be solved, demonstrating their role in exact sequences and homological algebra. Comparing these, \(\mathbb{Z}^n\) provides a straightforward, constructive example of free modules, whereas \(\mathbb{Q}\) over \(\mathbb{Z}\) illustrates the complex closure properties essential to injective modules.
Conclusion: Comparing Free and Injective Modules
Free modules are characterized by having a basis that allows every element to be uniquely expressed as a linear combination of basis elements, making them projective and highly structured. Injective modules, on the other hand, serve as essential extensions in exact sequences and are defined by their property that every homomorphism from a submodule can be extended to the whole module. Comparing free and injective modules reveals that free modules emphasize constructions and decompositions with bases, while injective modules focus on extension and embedding properties within module theory.
Free module and injective module Infographic
 libterm.com
libterm.com