Unrestricted grammar languages allow any string of symbols to be generated, representing the most powerful class in the Chomsky hierarchy. These languages are essential for modeling computations that require maximum expressiveness without constraints, often used in theoretical computer science. Discover how unrestricted grammar languages shape complex computational theories in the rest of this article.
Table of Comparison
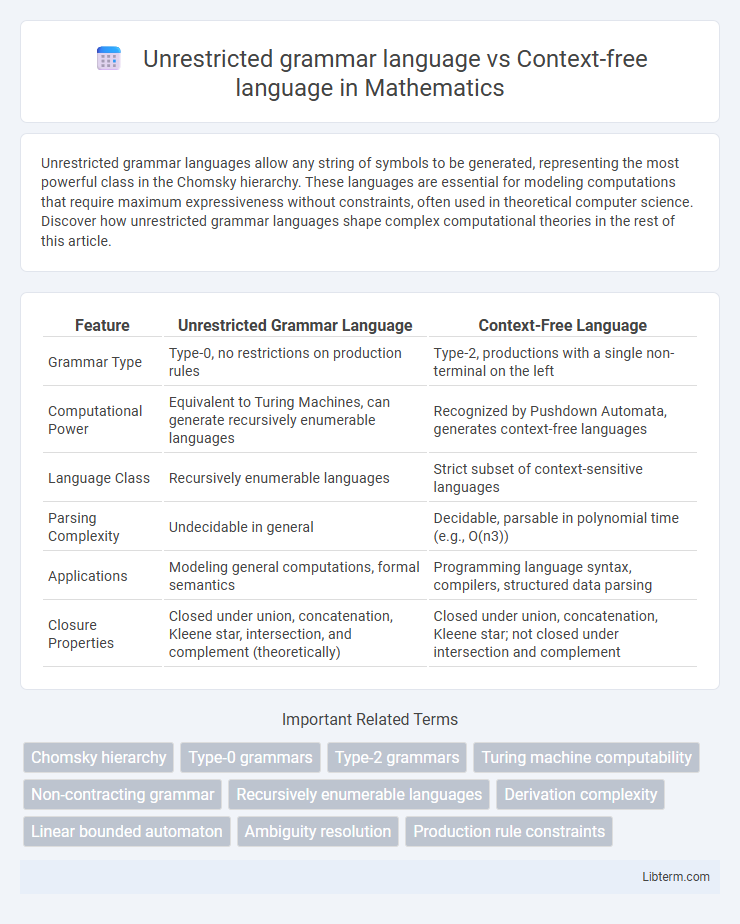
| Feature | Unrestricted Grammar Language | Context-Free Language |
|---|---|---|
| Grammar Type | Type-0, no restrictions on production rules | Type-2, productions with a single non-terminal on the left |
| Computational Power | Equivalent to Turing Machines, can generate recursively enumerable languages | Recognized by Pushdown Automata, generates context-free languages |
| Language Class | Recursively enumerable languages | Strict subset of context-sensitive languages |
| Parsing Complexity | Undecidable in general | Decidable, parsable in polynomial time (e.g., O(n3)) |
| Applications | Modeling general computations, formal semantics | Programming language syntax, compilers, structured data parsing |
| Closure Properties | Closed under union, concatenation, Kleene star, intersection, and complement (theoretically) | Closed under union, concatenation, Kleene star; not closed under intersection and complement |
Introduction to Formal Grammars
Unrestricted grammar languages, also known as Type 0 grammars, possess production rules with no constraints, enabling the generation of all recursively enumerable languages. Context-free languages, defined by Type 2 grammars, utilize production rules where a single nonterminal is replaced by a string of terminals and nonterminals, supporting efficient parsing algorithms. Formal grammars provide the foundational framework in automata theory to classify languages based on their generative power and computational complexity.
Defining Unrestricted Grammar Language
Unrestricted grammar language, also known as Type 0 language in the Chomsky hierarchy, is defined by grammars with no restrictions on production rules, allowing any string of symbols to be replaced by any other string. This makes unrestricted grammars more powerful than context-free grammars, which have productions with a single non-terminal on the left-hand side. Unrestricted grammar languages can describe all recursively enumerable languages, encompassing the full computational power of Turing machines.
Understanding Context-Free Language
Context-free languages are defined by context-free grammars where production rules replace a single non-terminal symbol with a string of terminals and non-terminals, enabling efficient parsing algorithms like the CYK algorithm and pushdown automata recognition. Unlike unrestricted grammars that generate recursively enumerable languages with rules that can have arbitrary string replacements, context-free grammars guarantee closure properties under union, concatenation, and Kleene star operations, making them essential in programming language syntax analysis. The inherent hierarchical structure of context-free languages allows for clear modeling of nested constructs such as balanced parentheses and arithmetic expressions, which cannot be reliably captured by regular languages or simple pattern matching.
Differences in Production Rules
Unrestricted grammar languages allow production rules with no limitations, enabling replacements of any substring with any other substring, making them more powerful for describing complex languages. Context-free languages restrict production rules to a single non-terminal on the left-hand side, which simplifies parsing and enables efficient algorithms like pushdown automata. This fundamental difference in production rule structure defines their computational complexity and practical applications in language processing.
Complexity and Computational Power
Unrestricted grammar languages, equivalent to recursively enumerable languages, have greater computational power than context-free languages, as they can describe any language recognizable by a Turing machine. The complexity of parsing unrestricted grammars is generally undecidable, making them infeasible for practical parsing algorithms. Context-free languages, recognized by pushdown automata, allow polynomial-time parsing algorithms such as the CYK algorithm, enabling efficient syntactic analysis in programming languages despite their lesser expressive power.
Language Recognition Capabilities
Unrestricted grammar languages encompass all formal languages decidable by a Turing machine, enabling the recognition of highly complex patterns beyond the capability of context-free languages (CFLs). Context-free languages, defined by context-free grammars and recognized by pushdown automata, are limited to hierarchical structures like balanced parentheses but cannot handle cross-serial dependencies or certain context-sensitive constructs. The superior recognition power of unrestricted grammars allows them to model any computable language, while context-free languages represent a strict subset, crucial for programming language parsing but insufficient for all language classes.
Real-world Applications of Each Language
Unrestricted grammar languages, also known as recursively enumerable languages, are crucial in modeling complex computational problems such as Turing machine simulations and advanced artificial intelligence algorithms where unrestricted rewriting rules provide maximum expressive power. Context-free languages find widespread use in programming languages, compilers, and natural language processing due to their efficient parsing algorithms and ability to represent nested structures like arithmetic expressions and syntactic constructs. Both language classes contribute fundamentally to software development, with unrestricted grammars enabling theoretical computation frameworks and context-free grammars underpinning practical syntax analysis and language design.
Limitations of Context-Free Languages
Context-free languages cannot adequately handle languages with arbitrary nesting and cross-serial dependencies, limiting their ability to model natural languages with complex syntax. They lack the expressive power to represent context-sensitive constructs such as agreement in number or gender and nested dependencies beyond simple recursive patterns. Unrestricted grammar languages, defined by Type-0 grammars in the Chomsky hierarchy, overcome these limitations by allowing rules that generate all recursively enumerable languages, thereby capturing more complex, context-sensitive language structures.
Unrestricted Grammar: Turing Completeness
Unrestricted grammars, also known as Type-0 grammars in the Chomsky hierarchy, are capable of generating languages recognized by Turing machines, making them Turing complete. Unlike context-free languages, which can be parsed by pushdown automata, unrestricted grammars allow production rules with no restrictions on the form, enabling the expression of complex computational processes. This Turing completeness means unrestricted grammars can represent any computable function, highlighting their fundamental role in theoretical computer science and formal language theory.
Choosing the Right Grammar for Language Processing
Unrestricted grammar languages, also known as Type-0 grammars, allow for maximum expressive power and can generate all recursively enumerable languages, making them suitable for complex language processing tasks requiring complete computational expressiveness. In contrast, context-free languages, generated by Type-2 grammars, offer efficient parsing algorithms like CYK and Earley parsers, enabling faster and more practical use in programming language compilers and natural language processing where hierarchical structure is essential. Choosing between unrestricted and context-free grammars involves balancing computational complexity and expressiveness, with context-free grammars generally preferred for tractability and unrestricted grammars reserved for modeling highly complex or unrestricted syntax patterns.
Unrestricted grammar language Infographic
 libterm.com
libterm.com