A right adjoint is a fundamental concept in category theory describing a functor that pairs with a left adjoint to establish a specific type of relationship between categories. Understanding how right adjoints preserve limits and reflect structure can deepen your grasp of mathematical abstractions. Explore the rest of the article to discover how right adjoints influence various fields like algebra and topology.
Table of Comparison
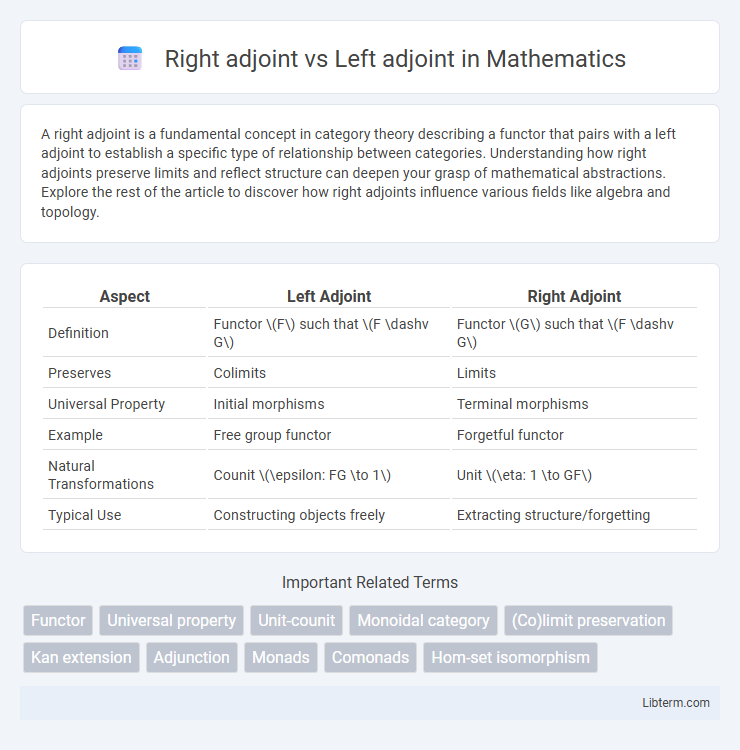
| Aspect | Left Adjoint | Right Adjoint |
|---|---|---|
| Definition | Functor \(F\) such that \(F \dashv G\) | Functor \(G\) such that \(F \dashv G\) |
| Preserves | Colimits | Limits |
| Universal Property | Initial morphisms | Terminal morphisms |
| Example | Free group functor | Forgetful functor |
| Natural Transformations | Counit \(\epsilon: FG \to 1\) | Unit \(\eta: 1 \to GF\) |
| Typical Use | Constructing objects freely | Extracting structure/forgetting |
Introduction to Adjoint Functors
Adjoint functors consist of a pair of functors, one left adjoint and one right adjoint, that establish a specific bijection between hom-sets in two categories, preserving structure in a reversible manner. The left adjoint functor often corresponds to a "free" or "generating" construction, while the right adjoint functor typically represents a "forgetful" or "underlying" process. This foundational concept in category theory formalizes a deep symmetry and duality between constructions and their universal properties.
Understanding Left Adjoint Functors
Left adjoint functors are key to category theory, providing a way to map objects and morphisms while preserving colimits, such as coproducts and coequalizers. They often arise in free constructions, like the free group functor left adjoint to the forgetful functor from groups to sets. Understanding left adjoints involves recognizing their universal property: for each object, they provide the most general way to extend a mapping from one category to another, making them central to many mathematical and computational frameworks.
Understanding Right Adjoint Functors
Right adjoint functors preserve limits and reflect the universal properties that define constructions such as products, equalizers, and pullbacks. They arise naturally when considering functors that reverse the direction of morphisms in a categorical context while maintaining structural coherence. Understanding right adjoint functors involves recognizing their role in establishing adjunctions where they serve as the limit-preserving partner to left adjoint functors, which preserve colimits.
Key Differences Between Left and Right Adjoints
Left adjoint functors preserve colimits such as coproducts and coequalizers, making them crucial for constructions that involve universal properties defined by colimits. Right adjoint functors preserve limits including products and equalizers, ensuring they respect structures characterized by limits. The fundamental difference lies in their preservation properties: left adjoints maintain colimits while right adjoints maintain limits, reflecting their dual roles in category theory.
Universal Properties and Their Roles
Right adjoints preserve limits and arise naturally from universal properties that characterize terminal or "best approximation" objects in a category, often representing solutions to extension problems. Left adjoints preserve colimits and are associated with universal properties that define initial or free constructions, providing canonical ways of generating structures from given data. Their roles in category theory are complementary, with right adjoints facilitating the extraction of structure via limits and left adjoints enabling the creation of objects via colimits, both governed by exact universal mapping properties.
Examples of Left Adjoint Functors
Left adjoint functors often arise in algebra and topology, exemplified by the free group functor from sets to groups, which assigns to each set the free group generated by it. Another classic example is the tensor product functor in module theory, where the tensor product with a fixed module is left adjoint to the Hom functor. These instances highlight how left adjoints construct freely generated structures by preserving colimits and facilitating universal properties.
Examples of Right Adjoint Functors
Right adjoint functors often arise in situations where a limiting process or a type of "universal mapping property" is involved, such as the inclusion functor from sets to topological spaces, which has a right adjoint given by the forgetful functor assigning to each topological space its underlying set. Another classical example is the "Hom" functor Hom(C, -), which is right adjoint to the tensor product functor - C in the context of module categories. These examples illustrate how right adjoints preserve limits and reflect structured data back to simpler categories.
Applications in Category Theory
Right adjoints preserve limits, making them essential in defining exponentials and constructing product-preserving functors in category theory. Left adjoints, which preserve colimits, are crucial for defining free constructions such as free groups and free algebras. Both adjoints facilitate the characterization of universal properties and provide foundational tools for functorial semantics and categorical equivalences.
Significance in Mathematical Structures
Right adjoint functors preserve limits and reflect essential properties in mathematical structures, often providing canonical constructions such as products and pullbacks. Left adjoint functors, by contrast, preserve colimits and generate free or universal objects like coproducts and pushouts, facilitating the building of new structures. The interplay between right and left adjoints reveals fundamental dualities and underpins the coherence and existence of various algebraic and topological constructions.
Summary: Choosing Right vs Left Adjoints
Right adjoints preserve limits and are typically used when implementing universal properties involving products or pullbacks, ensuring constructions remain stable under such operations. Left adjoints preserve colimits and often arise in contexts requiring free or extended structures, such as coproducts or pushouts. Choosing between right and left adjoints depends on whether the problem emphasizes limit preservation (favoring right adjoints) or colimit formation (favoring left adjoints) in categorical frameworks.
Right adjoint Infographic
 libterm.com
libterm.com