Morphism is a fundamental concept in mathematics and computer science that describes structure-preserving mappings between objects in categories, enabling the study of relationships and transformations. It plays a crucial role in fields like algebra, topology, and programming languages by providing a framework to analyze and compose complex systems efficiently. Discover how understanding morphisms can enhance Your grasp of abstract structures and their applications by reading the rest of the article.
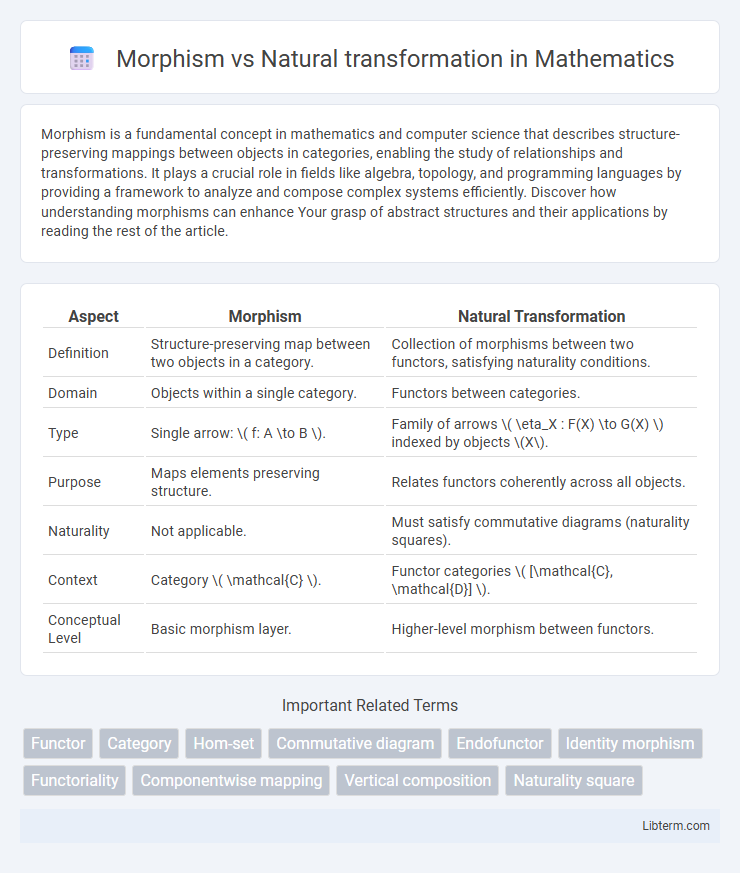
Table of Comparison
| Aspect | Morphism | Natural Transformation |
|---|---|---|
| Definition | Structure-preserving map between two objects in a category. | Collection of morphisms between two functors, satisfying naturality conditions. |
| Domain | Objects within a single category. | Functors between categories. |
| Type | Single arrow: \( f: A \to B \). | Family of arrows \( \eta_X : F(X) \to G(X) \) indexed by objects \(X\). |
| Purpose | Maps elements preserving structure. | Relates functors coherently across all objects. |
| Naturality | Not applicable. | Must satisfy commutative diagrams (naturality squares). |
| Context | Category \( \mathcal{C} \). | Functor categories \( [\mathcal{C}, \mathcal{D}] \). |
| Conceptual Level | Basic morphism layer. | Higher-level morphism between functors. |
Introduction to Morphisms and Natural Transformations
Morphisms represent structure-preserving maps between objects in categories, forming the fundamental building blocks of category theory by linking objects through algebraic or topological structures. Natural transformations provide a systematic way to compare functors, which are mappings between categories, by assigning morphisms to each object in a manner that respects the functorial structure. Understanding morphisms and natural transformations is crucial for analyzing how mathematical structures and processes interact coherently within and across categories.
Defining Morphisms in Category Theory
Morphisms in category theory represent structure-preserving maps between objects, formalizing the concept of functions in a categorical context. Each morphism has a specified domain and codomain, allowing compositions that satisfy associativity and identity laws within the category. Natural transformations, by contrast, are mappings between functors that assign to each object a morphism, preserving the categorical structure across entire diagrams and enabling comparisons between different functorial mappings.
Exploring the Role of Natural Transformations
Natural transformations serve as fundamental connections between functors in category theory, providing a structured way to compare different mappings between categories. Unlike morphisms that represent individual arrows within a category, natural transformations establish a coherent system of morphisms that respect the functorial structure across categories. This role is crucial for expressing equivalences, adjunctions, and dualities, thereby enriching the analysis of categorical frameworks.
Key Differences: Morphism vs Natural Transformation
A morphism is a structure-preserving map between objects within a single category, such as functions between sets or homomorphisms between groups. A natural transformation, however, is a morphism between functors, providing a way to transform one functor into another while respecting the internal structure of categories involved. Key differences include that morphisms act on objects directly within one category, whereas natural transformations operate between functors across categories, enforcing commutativity conditions as part of their definition.
Visualizing Morphisms and Natural Transformations
Visualizing morphisms involves representing arrows between objects in a category, emphasizing the structure-preserving relationships in mathematical contexts like sets, groups, or topological spaces. Natural transformations are visualized as a family of morphisms between functors, often depicted as commutative diagrams where arrows connect corresponding objects across categories, ensuring coherence conditions hold. These diagrams highlight how natural transformations provide a precise way to compare functors, capturing the notion of "naturality" through component-wise mappings that respect categorical composition.
Applications of Morphisms in Mathematics
Morphisms serve as fundamental structures in various branches of mathematics, enabling the representation of functions, homomorphisms, and maps that preserve algebraic, topological, or categorical properties. In category theory, morphisms facilitate the abstraction and analysis of relationships between objects, influencing areas like algebraic topology, algebraic geometry, and functional analysis. These applications highlight morphisms' role in encoding structure-preserving transformations, which underpin the study of mathematical objects and their interconnections.
Real-World Uses of Natural Transformations
Natural transformations enable seamless data migration across diverse database schemas, ensuring consistency and integrity in complex information systems. They facilitate modular software design by connecting different functors, allowing transformations between various programming paradigms like functional and object-oriented. These practical applications make natural transformations essential in optimizing compiler design, improving automated reasoning, and enhancing type theory implementations.
Importance in Functorial Relationships
Morphism in category theory defines a structure-preserving map between objects, enabling the study of their intrinsic relationships. Natural transformations extend this concept by providing a systematic way to compare functors, preserving the compositional framework across categories. Both morphisms and natural transformations play crucial roles in understanding and formalizing the interplay between functorial relationships, ensuring coherence and naturality in categorical constructions.
Examples Illustrating the Contrast
A morphism in category theory is a structure-preserving map between objects, such as a function between sets or a linear transformation between vector spaces, exemplified by a group homomorphism mapping elements while preserving group operations. In contrast, a natural transformation provides a way to transform one functor into another while respecting the internal structure of categories, illustrated by the natural transformation between the identity functor and the double functor on the category of sets, where each set maps to its double set. The key difference lies in morphisms acting between objects within a category, whereas natural transformations act between functors, preserving compositional relationships across categories.
Conclusion: Choosing Between Morphisms and Natural Transformations
Choosing between morphisms and natural transformations depends on the level of abstraction and the structure involved in category theory. Morphisms represent direct relationships between objects within a single category, while natural transformations capture relationships between functors and describe transformations between entire structures. For complex structures and higher-level abstractions, natural transformations provide a more powerful and flexible framework, whereas morphisms suffice for simpler, object-level mappings.
Morphism Infographic
 libterm.com
libterm.com