Coconjugate technology enhances the stability and efficacy of drugs by chemically linking two active compounds, resulting in improved therapeutic outcomes. This method optimizes drug delivery and minimizes side effects, benefiting your treatment experience significantly. Explore the rest of the article to discover how coconjugate strategies revolutionize modern medicine.
Table of Comparison
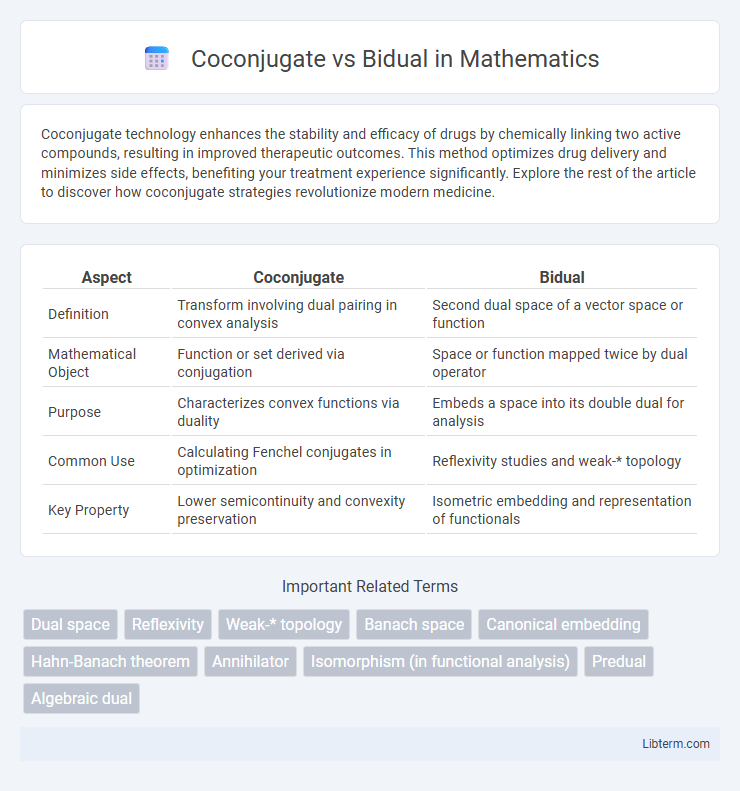
| Aspect | Coconjugate | Bidual |
|---|---|---|
| Definition | Transform involving dual pairing in convex analysis | Second dual space of a vector space or function |
| Mathematical Object | Function or set derived via conjugation | Space or function mapped twice by dual operator |
| Purpose | Characterizes convex functions via duality | Embeds a space into its double dual for analysis |
| Common Use | Calculating Fenchel conjugates in optimization | Reflexivity studies and weak-* topology |
| Key Property | Lower semicontinuity and convexity preservation | Isometric embedding and representation of functionals |
Introduction to Coconjugate and Bidual
Coconjugate and bidual concepts are fundamental in functional analysis, particularly in the study of dual spaces. The coconjugate refers to the conjugate mapping associated with a given operator, capturing how functionals interact with the original space. The bidual, or second dual space, consists of continuous linear functionals on the dual space, providing a natural extension and often enabling the identification of the original space within its double dual.
Defining the Coconjugate in Functional Analysis
The coconjugate in functional analysis is a mapping that assigns to each function its conjugate with respect to a dual pairing, often used in the context of convex analysis and optimization. It serves as a generalization of the Fenchel conjugate, capturing relationships between primal and dual spaces, and plays a key role in characterizing bidual functions. Understanding the coconjugate helps analyze properties such as lower semicontinuity, convexity, and the correspondence between a function and its bidual representation.
Understanding the Bidual of a Space
The bidual of a space, often denoted as X, is the dual of the dual space X*, representing all continuous linear functionals on X*. Coconjugate refers to operations or mappings related to dual spaces but emphasizes the relationship between the original space and its dual, especially in convex analysis contexts. Understanding the bidual aids in characterizing reflexive spaces where the natural embedding of X into X is surjective, providing insights into the space's completeness and structure.
Mathematical Foundations: Duals, Biduals, and Coconjugates
Coconjugates, biduals, and duals form fundamental constructs in functional analysis, particularly within the study of topological vector spaces and convex analysis. The dual of a vector space consists of all continuous linear functionals, while the bidual represents the dual of this dual space, often serving as a canonical embedding of the original space. Coconjugates extend these ideas by associating convex functions with their conjugates via Legendre-Fenchel transforms, providing essential tools for duality and optimization theory.
Key Differences between Coconjugate and Bidual
The key difference between coconjugate and bidual lies in their functional roles within convex analysis: the coconjugate function, also known as the Fenchel conjugate of a concave function, transforms the function into a convex one by reversing the domain and supremizing a linear form, whereas the bidual refers to the conjugate of the conjugate, often recovering the original function under convexity and lower semicontinuity conditions. The coconjugate emphasizes a single transformation from the primal to dual space, while the bidual represents a double transformation, bridging primal and dual spaces and providing a crucial tool for duality theory and optimization. Understanding these differences is essential for applying Fenchel duality, as the coconjugate pertains to function dualization, and the bidual reflects the reflexivity and closure properties of convex functions.
The Role in Banach and Reflexive Spaces
The coconjugate operator plays a critical role in Banach space theory by extending the dual space concept to analyze weak* topologies and compactness properties. In reflexive Banach spaces, the bidual operator acts as an isometric isomorphism, ensuring that each element in the double dual corresponds to a unique element in the original space. This interplay between coconjugate and bidual mappings helps characterize reflexivity and provides fundamental tools for operator theory and functional analysis.
Applications in Optimization and Convex Analysis
Coconjugate functions provide critical insights into dual problems by transforming primal convex functions under conjugation, enabling efficient characterization of optimal solutions in convex optimization. Bidual representations facilitate the recovery of the original convex function through double conjugation, ensuring strong duality holds in diverse optimization frameworks, including variational analysis and convex minimization. Practical applications involve leveraging coconjugate and bidual structures to analyze Fenchel duality, design proximal algorithms, and guarantee convergence properties in distributed optimization and economic equilibrium models.
Examples Illustrating Coconjugate vs Bidual
Consider the Banach space \( \ell^p \) with \( 1 < p < \infty \); its dual space is \( \ell^q \) where \( \frac{1}{p} + \frac{1}{q} = 1 \), illustrating the bidual relationship as \(\ell^p\) is isometrically isomorphic to a subspace of its bidual. In contrast, the coconjugate arises in convex analysis, where for a proper convex lower semicontinuous function \(f\), the coconjugate \(f^{\#}\) captures a transformation related to the conjugate \(f^*\), providing an alternative dual representation. Examples distinguishing these concepts highlight that biduals focus on space embeddings and structure, while coconjugates involve function transformations in duality theory.
Implications for Functional Analysis and Topology
Coconjugate and bidual spaces play crucial roles in functional analysis and topology by influencing the duality properties and reflexivity of Banach spaces. The coconjugate provides insights into the behavior of linear functionals under complex conjugation, affecting the structure of dual pairs, while the bidual often reveals whether a space is isometrically isomorphic to its double dual, highlighting reflexivity and compactness properties. Understanding the interplay between these concepts aids in characterizing weak topologies, dual operator theory, and the geometric aspects of normed spaces.
Conclusion: Significance of Coconjugate and Bidual
Coconjugates and bidual spaces play critical roles in functional analysis by revealing deep structural properties of Banach spaces. The coconjugate provides insights into the dual relationships underlying operators, while the bidual extends space completeness and facilitates reflexivity analysis. Together, these concepts enable advanced methods for characterizing space embeddings and continuity conditions in modern mathematical frameworks.
Coconjugate Infographic
 libterm.com
libterm.com