Preduals play a crucial role in functional analysis by providing the dual space from which a given Banach space arises, offering deep insights into its structure and properties. Understanding the relationship between a space and its predual helps analyze operator behavior and functional representations more effectively. Explore the rest of the article to discover how preduals impact various areas of mathematics and enhance your comprehension of this fundamental concept.
Table of Comparison
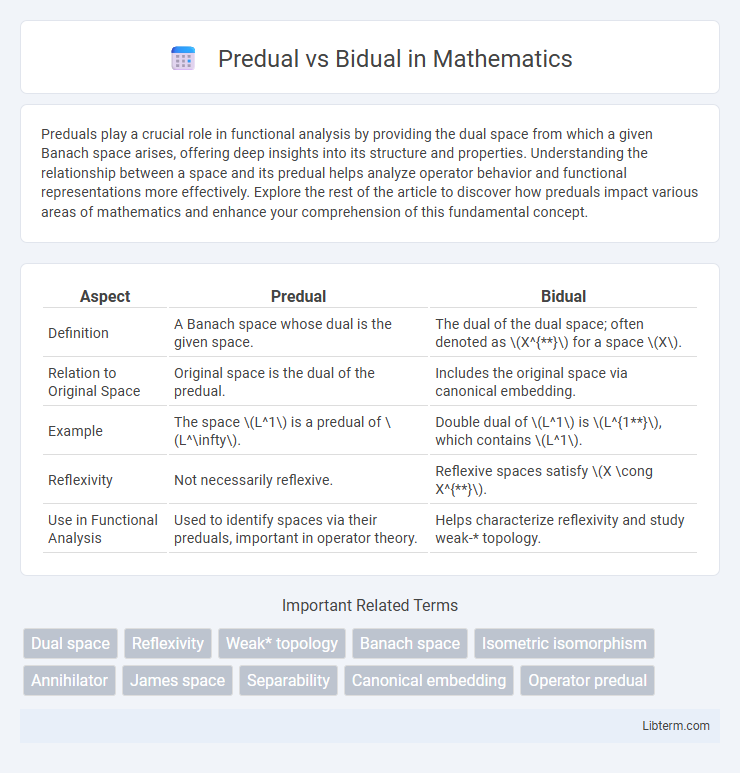
| Aspect | Predual | Bidual |
|---|---|---|
| Definition | A Banach space whose dual is the given space. | The dual of the dual space; often denoted as \(X^{}\) for a space \(X\). |
| Relation to Original Space | Original space is the dual of the predual. | Includes the original space via canonical embedding. |
| Example | The space \(L^1\) is a predual of \(L^\infty\). | Double dual of \(L^1\) is \(L^{1}\), which contains \(L^1\). |
| Reflexivity | Not necessarily reflexive. | Reflexive spaces satisfy \(X \cong X^{}\). |
| Use in Functional Analysis | Used to identify spaces via their preduals, important in operator theory. | Helps characterize reflexivity and study weak-* topology. |
Introduction to Predual and Bidual Concepts
Predual and bidual concepts play a crucial role in functional analysis, particularly in the study of Banach spaces and duality theory. A predual of a Banach space is a space whose dual is isometrically isomorphic to the given Banach space, providing a framework to analyze the original space through its dual relationships. The bidual, or second dual, of a Banach space is the dual space of its dual, often used to explore reflexivity and extend functional properties beyond the original space.
Definitions: What are Predual and Bidual?
Predual is a Banach space whose dual space corresponds to a given Banach space, serving as its "predecessor" in duality. Bidual refers to the double dual of a Banach space, denoted as the dual of the dual space, often providing a canonical embedding of the original space into its bidual. The relationship between predual and bidual spaces plays a crucial role in functional analysis and operator theory, especially in understanding reflexivity and dual space structures.
Historical Background and Development
The concepts of predual and bidual spaces emerged from the early 20th-century functional analysis, with foundational contributions by Stefan Banach and Hans Hahn. The development of preduals gained momentum through research on Banach space duality and reflexivity, particularly in the study of operator algebras and topological vector spaces during the mid-1900s. The bidual, or second dual, plays a critical role in understanding extensions of linear functionals and the structural properties of Banach spaces, influencing advances in modern analysis and quantum theory.
Predual Spaces: Key Properties
Predual spaces are Banach spaces whose duals can be identified with a given Banach space, playing a crucial role in functional analysis and operator theory. Key properties include reflexivity conditions where the predual uniquely determines the dual space structure, and the preservation of weak*-topologies under canonical embeddings. Understanding predual spaces facilitates the study of dual Banach spaces, particularly in contexts like von Neumann algebras and Lipschitz-free spaces.
Bidual Spaces: Fundamental Characteristics
Bidual spaces, also known as second duals, are formed by taking the dual of a Banach space's dual, revealing a richer structure that often extends beyond the original space. These spaces embed the original Banach space isometrically via the canonical embedding, providing insight into reflexivity and weak-* topology. The fundamental characteristic of bidual spaces lies in their ability to represent every continuous linear functional on the dual space, thereby facilitating advanced analysis in functional and operator theory.
Examples from Functional Analysis
In functional analysis, the predual of a Banach space X is a space Y such that X is the dual of Y, with classic examples including the relationship between L^1 spaces and L^ spaces, where L^1 serves as the predual of L^. The bidual of X, often denoted X, is the dual of the dual space X*, providing a natural embedding of X into X that is isometric but not always surjective, as seen in spaces like C([0,1]) where the bidual contains more functionals than can be represented by elements of the original space. Understanding preduals and biduals clarifies the structure of dual spaces, reflexivity, and weak* topologies in Banach spaces and operator algebras, with significant applications in the theory of von Neumann algebras where preduals characterize normal functionals.
Relationships Between Predual and Bidual
The predual of a Banach space X is a Banach space Y such that X is isometrically isomorphic to the dual space Y*. The bidual of X, denoted X, is the dual of the dual space X*, and there is a canonical embedding of X into X that is isometric but not always surjective. The relationship between predual and bidual highlights that if X has a unique predual Y, then X can be identified with Y* and the bidual X corresponds to Y; understanding these connections is crucial for investigating reflexivity and the structure of operator algebras.
Applications in Modern Mathematics
Preduals and biduals play crucial roles in modern functional analysis, particularly in the study of Banach spaces and operator algebras. Preduals help characterize dual spaces by identifying spaces whose duals are given Banach spaces, thus facilitating the analysis of weak-* topologies and reflexivity properties. Biduals extend spaces to their second duals, enabling the examination of double dual embeddings and the structure of reflexive and non-reflexive spaces, which are fundamental in optimization theory and quantum mechanics.
Challenges and Open Questions
Predual and bidual spaces present significant challenges in understanding their structural and functional properties, particularly in identifying conditions under which a Banach space admits a unique predual. The characterization of preduals often involves intricate duality mappings and topological constraints, complicating the analysis of reflexivity and weak* topology behaviors in bidual spaces. Open questions remain regarding the existence and classification of preduals for non-separable Banach spaces and the impact of these structures on operator theory and functional analysis frameworks.
Conclusion: Implications and Future Directions
The distinction between predual and bidual spaces significantly impacts functional analysis and operator theory, influencing the ways in which reflexivity and duality are characterized. Advanced research in this area may lead to refined structural understandings of Banach spaces, enhancing applications in optimization and quantum mechanics. Future directions involve exploring novel predual constructions and their ramifications on the stability of bidual topologies and their categorical equivalences.
Predual Infographic
 libterm.com
libterm.com