A distributive lattice is an algebraic structure where the operations of meet () and join () distribute over each other, ensuring a predictable interaction between elements. This property guarantees that every finite distributive lattice is isomorphic to the lattice of lower sets of some partially ordered set, making it a fundamental concept in order theory and lattice theory. Explore this article to understand how distributive lattices influence logic, computer science, and abstract algebra.
Table of Comparison
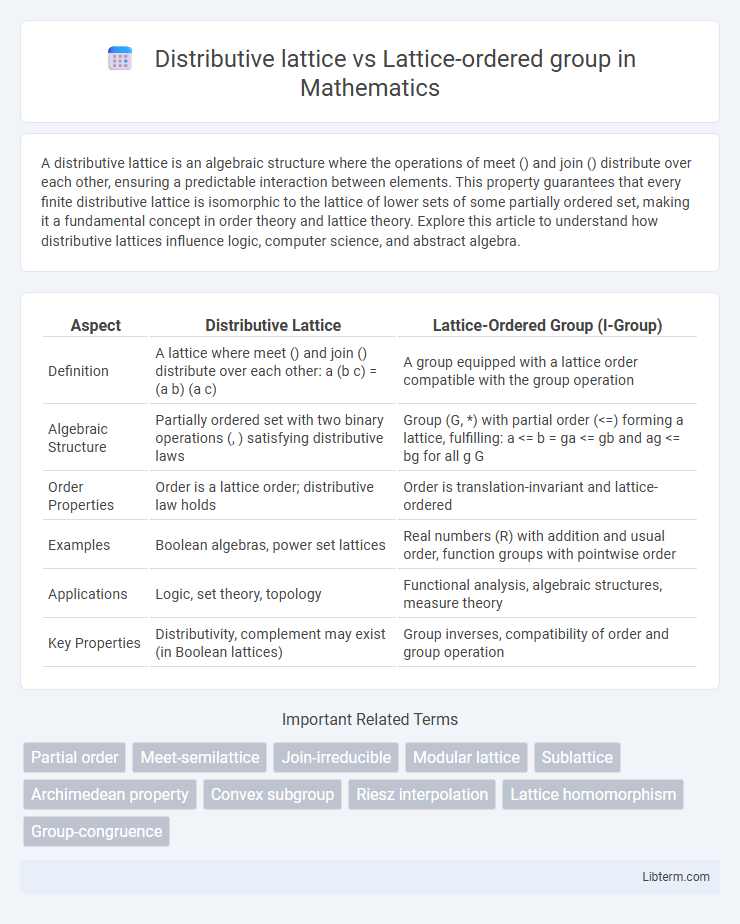
| Aspect | Distributive Lattice | Lattice-Ordered Group (l-Group) |
|---|---|---|
| Definition | A lattice where meet () and join () distribute over each other: a (b c) = (a b) (a c) | A group equipped with a lattice order compatible with the group operation |
| Algebraic Structure | Partially ordered set with two binary operations (, ) satisfying distributive laws | Group (G, *) with partial order (<=) forming a lattice, fulfilling: a <= b = ga <= gb and ag <= bg for all g G |
| Order Properties | Order is a lattice order; distributive law holds | Order is translation-invariant and lattice-ordered |
| Examples | Boolean algebras, power set lattices | Real numbers (R) with addition and usual order, function groups with pointwise order |
| Applications | Logic, set theory, topology | Functional analysis, algebraic structures, measure theory |
| Key Properties | Distributivity, complement may exist (in Boolean lattices) | Group inverses, compatibility of order and group operation |
Introduction to Lattice Theory
A distributive lattice is a partially ordered set in which every pair of elements has a unique supremum and infimum, and the operations of meet and join distribute over each other, forming a fundamental structure in lattice theory. Lattice-ordered groups (l-groups) extend these concepts by combining group operations with lattice orders, requiring the group operation to be compatible with the lattice order. Understanding the contrast between distributive lattices and lattice-ordered groups highlights the interplay between order theory and algebraic structures within lattice theory.
What is a Distributive Lattice?
A distributive lattice is an algebraic structure in which the operations of meet () and join () satisfy the distributive laws: a (b c) = (a b) (a c) and a (b c) = (a b) (a c). It forms a partially ordered set where every pair of elements has a unique least upper bound and greatest lower bound preserved under distribution. Unlike lattice-ordered groups, distributive lattices do not require group operations or inverses, focusing solely on the behavior of lattice operations under distribution.
Key Properties of Distributive Lattices
Distributive lattices are characterized by the key property that the operations of join (supremum) and meet (infimum) distribute over each other, ensuring that for all elements a, b, and c, the identity a (b c) = (a b) (a c) holds. This distributivity enforces a strong structural regularity absent in general lattice-ordered groups, where the group operation and lattice operations coexist but do not necessarily satisfy distributive laws. Distributive lattices form a crucial subclass of lattices with applications in order theory, algebra, and logic, distinguished by their unique interplay between order and algebraic operations.
Defining Lattice-ordered Groups
A lattice-ordered group (l-group) is an algebraic structure combining a group with a lattice such that the group operation is compatible with the lattice order, meaning the partial order is translation-invariant under group operations. Unlike distributive lattices, which focus solely on lattice operations satisfying distributive laws, l-groups require that the lattice order and group structure coexist harmoniously, enforcing order preservation under multiplication. This interplay allows for algebraic manipulation within a partially ordered set that adheres to both lattice and group axioms, enabling applications in order theory and functional analysis.
Structural Characteristics of Lattice-ordered Groups
Lattice-ordered groups (l-groups) combine group and lattice structures, characterized by an order-compatible group operation that respects the lattice order, enabling existence of suprema and infima for every pair of elements. Unlike distributive lattices, which are purely lattice-theoretic and require join and meet operations to distribute over each other, l-groups have a partially ordered group structure with lattice order, but their lattice is not necessarily distributive. The key structural characteristic is that the lattice order in l-groups is translation-invariant, meaning that adding group elements preserves the order, making them central in studying ordered algebraic systems and functional analysis.
Major Differences Between Distributive Lattices and Lattice-ordered Groups
Distributive lattices are algebraic structures where the meet and join operations satisfy the distributive laws, ensuring the order and combination of elements follow strict distributive properties. Lattice-ordered groups (l-groups) combine lattice and group structures, allowing elements to be compared and combined under group operations with a compatible lattice order, but do not require distributivity between meet and join. The major difference lies in the algebraic framework: distributive lattices emphasize distributive laws in order theory, while lattice-ordered groups integrate group theory constraints with lattice ordering without enforcing distributivity.
Examples and Illustrations
A distributive lattice is exemplified by the set of natural numbers under the operations of minimum and maximum, illustrating the distributive property: meet distributes over join. In contrast, lattice-ordered groups (l-groups) such as the group of real numbers with addition and the usual order combine group structure with lattice order, where the lattice operations respect the group operation. Illustrations include the integer group Z as an l-group with the natural order and lattice operations defined by minimum and maximum, highlighting the integration of algebraic and order-theoretic properties.
Applications in Mathematics and Beyond
Distributive lattices provide foundational structures for data organization in computer science, logic, and topology, enabling efficient algorithms in decision-making and information retrieval. Lattice-ordered groups extend group theory with order structure, crucial in functional analysis, measure theory, and economics for modeling optimization and resource allocation. Both frameworks facilitate advancements in algebraic geometry, cryptography, and theoretical physics through their unique handling of order and algebraic operations.
Advantages and Limitations of Each Structure
A distributive lattice offers clear advantages in simplifying algebraic expressions and supports unique factorization, making it ideal for logical frameworks and order theory applications, but it lacks the algebraic richness to model group symmetries or handle invertible elements. Lattice-ordered groups (l-groups) provide a robust structure combining group operations with lattice order, enabling the study of ordered algebraic systems with inverses and facilitating applications in functional analysis and group theory, though their complexity can hinder straightforward factorization and requires more intricate axiomatic frameworks. The choice between distributive lattices and lattice-ordered groups hinges on the need for either simpler order-theoretic properties or more comprehensive algebraic structures supporting group operations under lattice order.
Conclusion: Choosing the Right Approach
Distributive lattices ensure that meet and join operations distribute over each other, providing a simpler algebraic framework ideal for modeling hierarchical data and logic systems. Lattice-ordered groups extend this structure by integrating group operations with lattice order, offering greater flexibility for applications requiring both algebraic group properties and ordered structures, such as in certain optimization and theoretical physics contexts. Selecting between these approaches depends on whether the problem demands purely distributive order properties or a combination of order and group operations for richer algebraic manipulation.
Distributive lattice Infographic
 libterm.com
libterm.com