Exponential growth describes a process where quantities increase at a consistent rate over time, leading to rapidly escalating outcomes that far exceed linear growth patterns. This concept applies to various fields such as finance, population dynamics, and technology advancements, highlighting the powerful impact of compounding. Explore the rest of the article to understand how exponential trends influence your decisions and future possibilities.
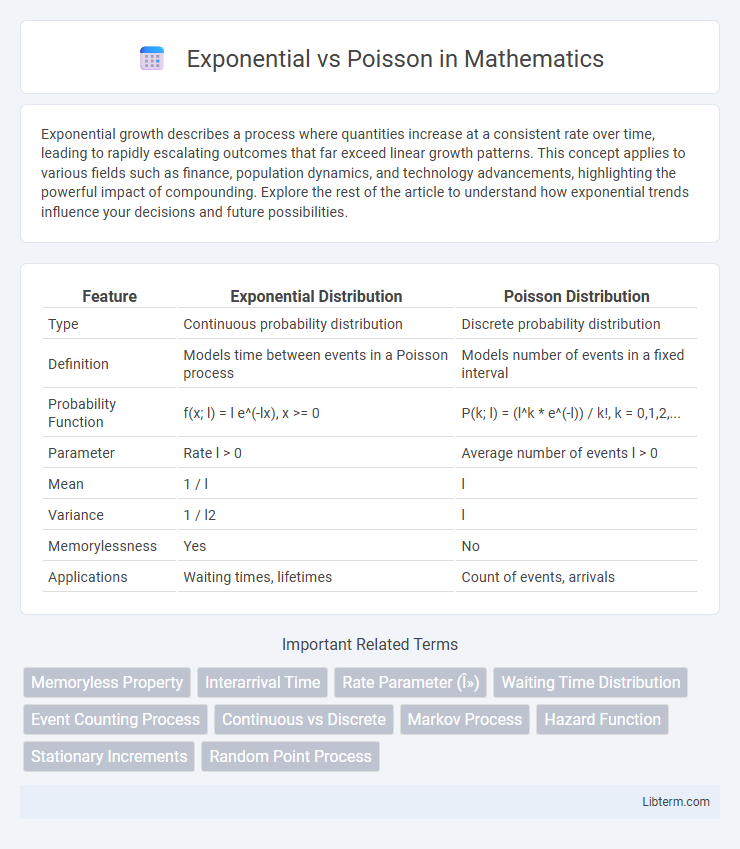
Table of Comparison
| Feature | Exponential Distribution | Poisson Distribution |
|---|---|---|
| Type | Continuous probability distribution | Discrete probability distribution |
| Definition | Models time between events in a Poisson process | Models number of events in a fixed interval |
| Probability Function | f(x; l) = l e^(-lx), x >= 0 | P(k; l) = (l^k * e^(-l)) / k!, k = 0,1,2,... |
| Parameter | Rate l > 0 | Average number of events l > 0 |
| Mean | 1 / l | l |
| Variance | 1 / l2 | l |
| Memorylessness | Yes | No |
| Applications | Waiting times, lifetimes | Count of events, arrivals |
Introduction to Exponential and Poisson Distributions
The Exponential distribution models the time between events in a Poisson process, characterized by a single rate parameter l representing the event occurrence rate. The Poisson distribution quantifies the number of events occurring within a fixed interval of time or space, also parameterized by l as the average event rate. Both distributions are fundamentally linked, with the Exponential describing inter-arrival times and the Poisson describing event counts.
Key Definitions and Concepts
The Exponential distribution models the time between independent events occurring at a constant average rate, characterized by its memoryless property and parameter lambda (l), which represents the event rate. The Poisson distribution describes the probability of a given number of events happening in a fixed interval of time or space, with the parameter lambda (l) indicating the expected number of events per interval. Both distributions are interconnected; the Exponential distribution models inter-arrival times in a Poisson process, where events occur randomly and independently with a consistent average rate.
Mathematical Formulations
Exponential distribution is mathematically described by the probability density function \( f(x; \lambda) = \lambda e^{-\lambda x} \) for \( x \geq 0 \), characterizing the time between Poisson process events. Poisson distribution is given by the probability mass function \( P(k; \lambda) = \frac{\lambda^k e^{-\lambda}}{k!} \), representing the number of events in a fixed interval. The parameter \( \lambda \) serves as the rate in both distributions, linking the expected count in Poisson to the intensity parameter of the Exponential interarrival times.
Real-World Applications
The Exponential distribution models the time between independent events in a Poisson process, commonly applied in estimating wait times in call centers and reliability testing of electronic components. The Poisson distribution quantifies the probability of a given number of events occurring within a fixed interval, frequently used in traffic flow analysis, insurance claim modeling, and counting radioactive decay events. Both distributions are integral in queuing theory, telecommunications, and risk management, enabling precise predictions under varying conditions of event randomness.
Relationship Between Exponential and Poisson
The Exponential and Poisson distributions are intrinsically linked through the modeling of events in a Poisson process, where the Poisson distribution counts the number of events in a fixed interval, and the Exponential distribution models the waiting time between those events. Specifically, the Exponential distribution's memoryless property describes the time between successive events in a Poisson process occurring at a constant rate l, making its probability density function f(t) = le^(-lt). Understanding this relationship is crucial for applications in queuing theory, reliability engineering, and stochastic processes where event timings and counts need accurate probabilistic descriptions.
Differences in Usage Scenarios
Exponential distributions model the time between independent events in a continuous process, making them ideal for analyzing waiting times in systems like radioactive decay or customer service. Poisson distributions count the number of events occurring within a fixed interval, commonly applied to rare occurrences such as call arrivals at a call center or traffic accidents. The Exponential distribution emphasizes event timing, whereas the Poisson distribution focuses on event frequency.
Parameter Interpretation
The exponential distribution's parameter, typically denoted as lambda (l), represents the rate or frequency of events occurring per unit time, defining the waiting time between events in a Poisson process. In contrast, the Poisson distribution's parameter lambda (l) quantifies the expected number of events in a fixed interval, indicating the event count probability. Both distributions share l but interpret it differently: as an event rate for exponential and as an event count mean for Poisson.
Visualizing Probability Distributions
Visualizing probability distributions of Exponential and Poisson distributions highlights their distinct characteristics in modeling events. The Exponential distribution presents a continuous, decreasing curve illustrating the time between events, emphasizing its memoryless property. In contrast, the Poisson distribution exhibits discrete probability masses representing the count of events occurring within a fixed interval, making it ideal for modeling rare or random event occurrences.
Common Misconceptions
Exponential and Poisson distributions are often confused due to their connection in modeling event timings, but the Exponential distribution describes the time between events in a Poisson process, not the number of events itself. A common misconception is that the Poisson distribution measures the likelihood of the exact timing of events, while it actually models the count of events within a fixed interval. Understanding that the Poisson quantifies event frequency and the Exponential focuses on interarrival times clarifies their distinct applications in stochastic processes.
Summary and Conclusion
The exponential distribution models the time between events in a continuous, memoryless process, characterized by a constant hazard rate, while the Poisson distribution describes the probability of a given number of events occurring in a fixed interval of time or space. These distributions are closely related; the Poisson counts the number of events, and the exponential models the waiting times between these events under a Poisson process framework. Understanding their distinct roles enhances analysis in fields like telecommunications, queueing theory, and reliability engineering.
Exponential Infographic
 libterm.com
libterm.com