A ring symbolizes commitment, style, and personal expression through its design and materials. Choosing the perfect ring involves considering factors like metal type, gemstone quality, and craftsmanship to match your unique taste and occasion. Explore the rest of the article to discover expert tips on selecting and caring for your ideal ring.
Table of Comparison
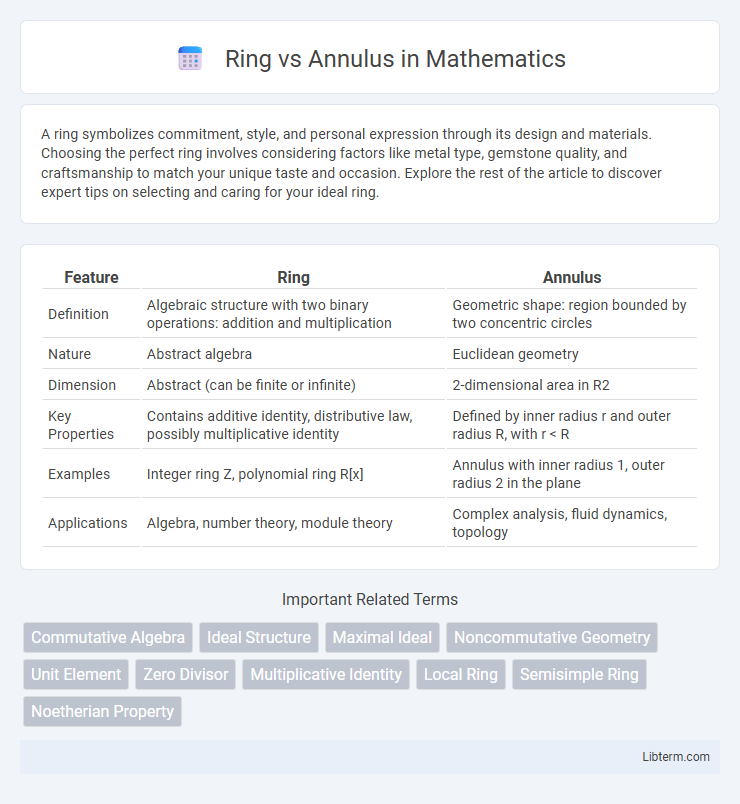
| Feature | Ring | Annulus |
|---|---|---|
| Definition | Algebraic structure with two binary operations: addition and multiplication | Geometric shape: region bounded by two concentric circles |
| Nature | Abstract algebra | Euclidean geometry |
| Dimension | Abstract (can be finite or infinite) | 2-dimensional area in R2 |
| Key Properties | Contains additive identity, distributive law, possibly multiplicative identity | Defined by inner radius r and outer radius R, with r < R |
| Examples | Integer ring Z, polynomial ring R[x] | Annulus with inner radius 1, outer radius 2 in the plane |
| Applications | Algebra, number theory, module theory | Complex analysis, fluid dynamics, topology |
Understanding Rings and Annuli: Definitions
A ring is an algebraic structure consisting of a set equipped with two binary operations, addition and multiplication, where addition forms an abelian group and multiplication is associative. An annulus is a topological space shaped like a ring, defined as the region bounded by two concentric circles in a plane, representing a distinct geometric concept. Understanding rings involves abstract algebraic properties, while annuli pertain to geometric and topological characteristics.
Key Geometric Differences Between Ring and Annulus
A ring is a broader term referring to any circular band or loop, often in various dimensions and contexts, while an annulus specifically denotes a planar figure bounded by two concentric circles. The annulus is defined by the difference in radii between its outer and inner circles, creating a flat, two-dimensional shape with a precise area equal to p(R2 - r2), where R is the outer radius and r is the inner radius. Rings can exist in three dimensions, such as toruses, and do not necessarily require concentric boundaries, distinguishing them from the strictly planar and concentric nature of annuli.
Mathematical Representation of a Ring
A ring in mathematics is often represented as a set equipped with two binary operations: addition and multiplication, satisfying properties such as associativity, distributivity, and the existence of additive identity and inverses. Unlike an annulus, which is a geometric region bounded by two concentric circles in Euclidean space, a mathematical ring is an algebraic structure fundamental in abstract algebra, including examples like integers modulo n. The formal definition involves a set R with operations (+) and (x) where (R, +) forms an abelian group and multiplication is associative, making it a versatile construct in number theory and algebraic geometry.
Mathematical Representation of an Annulus
An annulus is mathematically represented as the region between two concentric circles with different radii, defined by the inequality r < (x2 + y2) < R, where r and R are the inner and outer radii respectively. This geometric shape differs from a ring in that the annulus includes the continuous area bounded by these two circles, excluding their interiors. The area of an annulus is calculated using the formula p(R2 - r2), highlighting the subtraction of the smaller circle's area from the larger one.
Common Applications of Rings in Mathematics and Engineering
Rings, algebraic structures consisting of sets equipped with two binary operations satisfying specific properties, play a crucial role in various mathematical disciplines including abstract algebra, number theory, and cryptography. Engineers utilize rings in coding theory, error detection, and system design to model cyclic structures and symmetry in mechanical and electrical systems. Unlike annuli, which describe geometric ring-shaped regions, rings provide an abstract framework essential for solving polynomial equations and designing digital communication systems.
Annulus: Properties and Real-World Uses
An annulus, defined as the region bounded by two concentric circles, possesses unique geometric properties including its area calculated by the difference of the squares of the radii, \( A = \pi(R^2 - r^2) \). This shape is fundamental in engineering and physics, notably in designing washers, gaskets, and drilling rigs where stress distribution and fluid flow are critical. Annuli also play a crucial role in optical systems and mechanical seals, optimizing both functionality and material efficiency.
Calculating Area: Ring vs Annulus
The area of a ring is calculated by subtracting the area of the inner circle from the area of the outer circle, expressed as p(R2 - r2), where R is the outer radius and r is the inner radius. Similarly, the annulus refers to the region bounded by two concentric circles, and its area is also found using the formula p(R2 - r2). Both terms describe the same geometric shape, and the calculation involves determining the difference in the areas of the two circles based on their respective radii.
Visualizing Rings and Annuli: Diagrams and Examples
Visualizing rings and annuli often involves diagrams featuring concentric circles, where a ring represents the entire area bounded by two circles, while an annulus corresponds specifically to the region between them. Diagrams typically use shading or color differentiation to highlight the annulus, emphasizing the space between the inner and outer circles, which is essential in understanding topology and geometry concepts. Examples include representing ring-shaped objects or analyzing annular regions in physics and engineering to illustrate properties like area and boundary behavior.
Common Misconceptions: Ring vs Annulus
A common misconception between ring and annulus is that both terms are interchangeable when describing geometric regions. A ring generally refers to any shape resembling a circular band, whereas an annulus is specifically the region between two concentric circles with different radii. Understanding this distinction is crucial in fields like mathematics and engineering where precise terminology affects calculations involving area and boundary conditions.
Summary Table: Ring vs Annulus Comparison
The summary table comparing Ring vs Annulus highlights key differences in geometric definitions, with a ring defined as a shape bounded by two concentric circles characterized by inner and outer radii, while an annulus specifically refers to the planar region between these two concentric circles. Parameters such as area calculation differ, where the ring's area is the difference between the outer and inner circle areas, computed as p(R2 - r2), and the annulus shares this formula but emphasizes its use in applications like engineering and physics. The comparison also notes distinctions in terminology usage across disciplines, with "ring" often applied in algebra and topology contexts, whereas "annulus" is predominantly favored in geometry and complex analysis.
Ring Infographic
 libterm.com
libterm.com