The fundamental group is a key concept in algebraic topology that captures the essential features of a space's shape by analyzing loops based at a point. This group helps distinguish topological spaces through their path-connectedness and loop homotopy classes. Explore the rest of the article to understand how the fundamental group applies to various geometric structures and your study of topology.
Table of Comparison
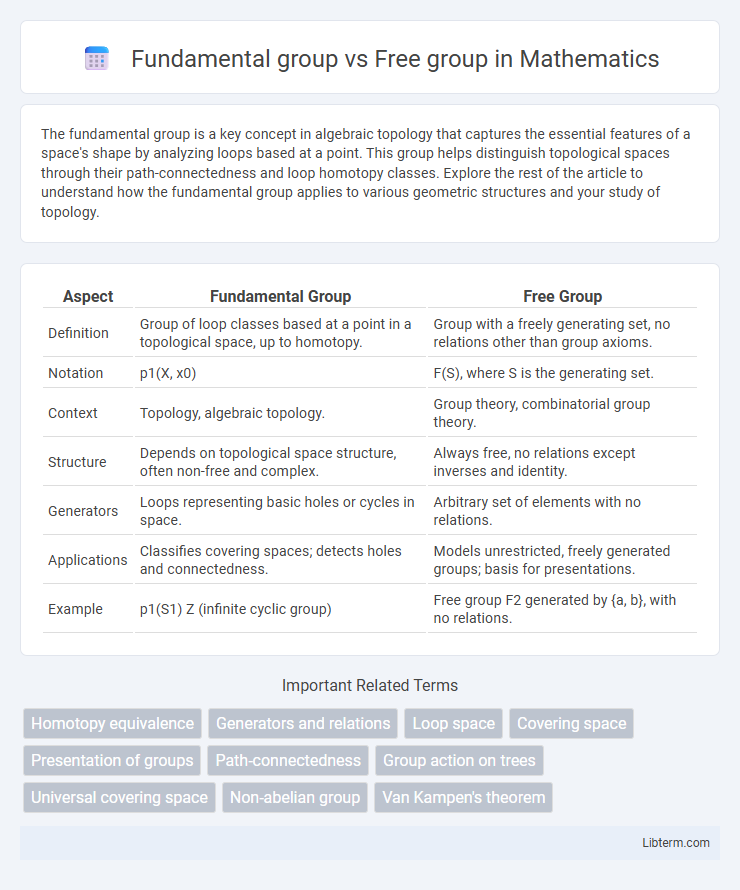
| Aspect | Fundamental Group | Free Group |
|---|---|---|
| Definition | Group of loop classes based at a point in a topological space, up to homotopy. | Group with a freely generating set, no relations other than group axioms. |
| Notation | p1(X, x0) | F(S), where S is the generating set. |
| Context | Topology, algebraic topology. | Group theory, combinatorial group theory. |
| Structure | Depends on topological space structure, often non-free and complex. | Always free, no relations except inverses and identity. |
| Generators | Loops representing basic holes or cycles in space. | Arbitrary set of elements with no relations. |
| Applications | Classifies covering spaces; detects holes and connectedness. | Models unrestricted, freely generated groups; basis for presentations. |
| Example | p1(S1) Z (infinite cyclic group) | Free group F2 generated by {a, b}, with no relations. |
Introduction to Fundamental Groups and Free Groups
Fundamental groups capture the essential loop structures in topological spaces by classifying paths based on continuous deformation, serving as a pivotal tool in algebraic topology. Free groups are algebraic constructs generated by sets without relations, allowing unrestricted combination of elements and their inverses, making them foundational in group theory. Understanding the connection between fundamental groups and free groups reveals how complex topological features can be interpreted as algebraic objects generated freely by loops in a space.
Definitions: What is a Fundamental Group?
The fundamental group, denoted p1(X, x0), is a topological invariant that captures the algebraic structure of loops based at a point x0 in a topological space X, up to homotopy equivalence. It consists of equivalence classes of continuous maps from the unit interval [0,1] into X that start and end at x0, with group operation defined by path concatenation. In contrast, a free group is an algebraic construct generated by a set of elements with no relations except those required by group axioms, serving as an abstract model for fundamental groups of certain spaces like bouquets of circles.
Understanding Free Groups: Key Concepts
Free groups are algebraic structures generated by a set where elements combine without relations other than inverses and identity, serving as foundational examples in group theory. Fundamental groups, associated with topological spaces, describe loops up to homotopy and often emerge as quotients of free groups by imposing relations derived from the space's topology. Understanding free groups clarifies how more complex groups, like fundamental groups, arise by introducing relations that capture geometric constraints.
Fundamental Group: Topological Foundations
The fundamental group is a topological invariant that captures the essential loop structures in a given space, classifying paths up to continuous deformation and thus providing insights into the space's shape and connectivity. It forms a group under the operation of path concatenation, reflecting the space's underlying topological structure and enabling the study of covering spaces, homotopy, and algebraic topology. Unlike free groups, fundamental groups may have complex relations originated from the topology of the space, making them crucial for understanding properties such as holes, loops, and connectivity in geometric and topological contexts.
Algebraic Structure of Free Groups
The fundamental group captures topological properties of a space by classifying loops up to homotopy, forming a group that reflects the space's shape. Free groups, defined algebraically by a set of generators without relations, provide a straightforward model of group structure where every element can be uniquely written as a reduced word in these generators. The algebraic structure of free groups is characterized by their basis, enabling the decomposition of any group element into a product of generator powers with no defining relations, making free groups a universal building block in combinatorial group theory.
Comparing Generators and Relations
The fundamental group is defined by loops based at a point in a topological space, where its generators correspond to equivalence classes of these loops under homotopy, and relations arise from continuous deformations of loops, reflecting the space's topological structure. Free groups consist of generators with no relations except those necessary for group axioms, meaning their elements represent all possible finite combinations of generators and their inverses without additional constraints. Comparing both, the fundamental group generally has relations encoded by the space's topology, while free groups have a minimal presentation with generators only, highlighting fundamental groups as quotients of free groups by normal subgroups generated by these relations.
Key Differences: Fundamental vs Free Groups
The fundamental group captures the topological structure of a space by encoding loops based at a point up to homotopy, while the free group is an algebraic construct generated by a set without relations. Unlike the fundamental group, which can have complex relations reflecting the space's connectivity, the free group is defined solely by generators with no defining relations. Key differences include the fundamental group's dependence on the space's geometry, contrasted with the free group's purely algebraic nature and universal property among group homomorphisms from the generating set.
Examples: Fundamental Group vs Free Group Applications
The fundamental group captures the topological properties of a space by representing loops based at a point, as seen in the fundamental group of a circle, which is isomorphic to the free group on one generator, reflecting its simple loop structure. Free groups play a crucial role in algebraic topology by modeling the fundamental group of wedge sums of circles, where the fundamental group is a free group with a rank equal to the number of circles. Applications include classifying covering spaces, where the fundamental group of a space determines the types of covering spaces, and in combinatorial group theory, where free groups serve as building blocks for more complex group structures.
Significance in Algebraic Topology
The fundamental group captures the essential topological features of a space by encoding loop structures up to homotopy, serving as a primary invariant in algebraic topology. Free groups provide a flexible, algebraically simple model with a basis of independent generators, crucial for understanding spaces with a wedge of circles or graphs by representing their fundamental groups. The interplay between fundamental groups and free groups allows for classification of spaces, computation of covering spaces, and analysis of homotopical properties in algebraic topology.
Conclusion: Choosing the Right Group for Your Problem
The fundamental group captures topological properties of spaces by encoding loops up to homotopy, making it essential for problems in algebraic topology and geometric analysis. Free groups, characterized by their unrestricted generators and lack of relations, provide a versatile algebraic framework for group theory and combinatorial problems. Selecting between fundamental and free groups depends on whether the problem requires topological invariants or purely algebraic structures for effective modeling and solution.
Fundamental group Infographic
 libterm.com
libterm.com