Strong topology defines the finest topology on a space ensuring continuity of a given family of functions, often used in functional analysis and vector spaces. It plays a crucial role in understanding convergence and continuity properties in infinite-dimensional spaces. Explore the rest of the article to deepen your comprehension of how strong topology impacts various mathematical and applied contexts.
Table of Comparison
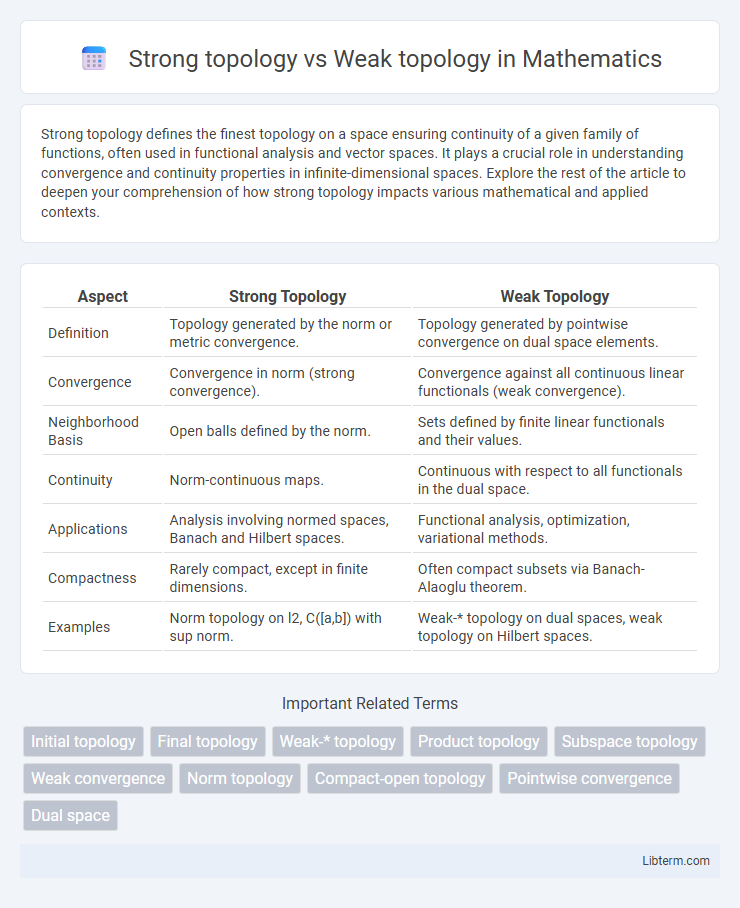
| Aspect | Strong Topology | Weak Topology |
|---|---|---|
| Definition | Topology generated by the norm or metric convergence. | Topology generated by pointwise convergence on dual space elements. |
| Convergence | Convergence in norm (strong convergence). | Convergence against all continuous linear functionals (weak convergence). |
| Neighborhood Basis | Open balls defined by the norm. | Sets defined by finite linear functionals and their values. |
| Continuity | Norm-continuous maps. | Continuous with respect to all functionals in the dual space. |
| Applications | Analysis involving normed spaces, Banach and Hilbert spaces. | Functional analysis, optimization, variational methods. |
| Compactness | Rarely compact, except in finite dimensions. | Often compact subsets via Banach-Alaoglu theorem. |
| Examples | Norm topology on l2, C([a,b]) with sup norm. | Weak-* topology on dual spaces, weak topology on Hilbert spaces. |
Introduction to Topological Concepts
Strong topology refines the structure of a space by generating open sets through norm-induced metrics, ensuring convergence in norm implies topological convergence. Weak topology, defined by convergence of all continuous linear functionals, produces fewer open sets, allowing sequences to converge in a weaker sense without norm convergence. These contrasting topologies provide essential frameworks in functional analysis, influencing continuity, compactness, and convergence behaviors.
Defining Strong and Weak Topologies
Strong topology on a vector space is defined by the family of seminorms that induce convergence based on norm or metric, ensuring every neighborhood contains a norm-open set. Weak topology, on the other hand, is generated by the collection of all continuous linear functionals, making it the coarsest topology for which all these functionals remain continuous. Strong topology produces finer convergence criteria, while weak topology emphasizes continuity relative to linear functionals and is generally coarser.
Historical Background and Motivation
Strong topology and weak topology originated from the study of functional analysis in the early 20th century, particularly in the context of infinite-dimensional vector spaces and duality theory. The weak topology was motivated by the need to analyze convergence of functionals and operators with respect to pointwise convergence on dual spaces, while the strong topology emerged to capture norm convergence and provide a finer topology that reflects the full metric structure of normed spaces. These topologies were fundamental in the development of Banach and Hilbert space theory, influencing modern analysis and applications in differential equations and optimization.
Key Differences Between Strong and Weak Topologies
Strong topology on a vector space is generated by the family of seminorms that define the space, ensuring convergence implies norm convergence and typically resulting in a finer topology. Weak topology, induced by the dual space, is coarser, with convergence only requiring convergence of all continuous linear functionals. The key difference lies in their convergence criteria: strong topology needs norm convergence, while weak topology demands only pointwise convergence on the dual, affecting compactness and continuity properties significantly.
Examples in Functional Analysis
In functional analysis, the strong topology on a Banach space X is defined by the norm, where convergence means that the norm of the difference goes to zero, such as in L^p spaces for 1 <= p < , where strong convergence implies convergence in norm. The weak topology, generated by all continuous linear functionals, is weaker and examples include sequences in l^2 that converge weakly but not strongly, demonstrating weak convergence as pointwise convergence of all functionals. Weak* topology, important in dual spaces like l^\infty, shows further relaxation, where bounded sequences converge in the weak* sense, exemplified by the Banach-Alaoglu theorem ensuring compactness in the dual unit ball.
Convergence in Strong vs Weak Topology
Convergence in the strong topology requires that a sequence or net converges with respect to the norm, meaning the norm difference between the elements and the limit goes to zero. In contrast, convergence in the weak topology only demands convergence of all continuous linear functionals applied to the sequence, resulting in weaker conditions that allow sequences to converge without norm convergence. This distinction is fundamental in functional analysis, affecting the structure and compactness properties of Banach and Hilbert spaces.
Compactness: Strong vs Weak Perspective
Compactness in the strong topology implies sequential compactness and often aligns with norm convergence, providing robust control over limit points. In contrast, the weak topology's compact sets are characterized by the Banach-Alaoglu theorem, where the unit ball in the dual space is weak*-compact but not necessarily strongly compact. This distinction highlights that weak compactness is more general and less restrictive, allowing for greater applicability in functional analysis and infinite-dimensional spaces.
Applications in Mathematics and Physics
Strong topology is essential in functional analysis for studying continuity and convergence of operators in normed vector spaces, enabling precise characterization of solution stability in differential equations. Weak topology, pivotal in optimization and variational problems, allows convergence analysis in infinite-dimensional spaces by focusing on functional evaluations rather than norm convergence, facilitating compactness arguments in Banach and Hilbert spaces. In physics, strong topology supports rigorous formulations of quantum state evolutions, while weak topology underpins quantum measurement theory and statistical mechanics by describing convergence of state sequences in dual spaces.
Advantages and Limitations
Strong topology offers finer convergence criteria, enabling more precise control over limits in normed spaces, which benefits functional analysis and operator theory. Weak topology provides greater compactness and weaker convergence conditions, facilitating analysis in infinite-dimensional spaces and optimization problems. However, strong topology may lack compactness, limiting applications in infinite dimensions, while weak topology's convergence can be less intuitive and slower, affecting numerical computations.
Summary and Further Reading
Strong topology is defined by the norm convergence on a vector space, making it finer and stronger compared to the weak topology, which is defined by pointwise convergence on the dual space and is weaker but often easier to handle in infinite-dimensional analysis. Understanding their interplay is crucial in functional analysis, particularly in studying dual spaces, operator theory, and convergence of sequences or nets. For deeper insight, consult standard texts like Rudin's "Functional Analysis," Conway's "A Course in Functional Analysis," and Megginson's "An Introduction to Banach Space Theory," which provide comprehensive coverage of topological vector spaces and their applications.
Strong topology Infographic
 libterm.com
libterm.com