Geodesic domes are architectural marvels characterized by a network of triangles that distribute structural stress evenly, creating lightweight yet incredibly strong constructions. Their design maximizes space efficiency and energy conservation, making them ideal for sustainable living and innovative building projects. Discover how geodesic principles can transform your architectural approach by reading the rest of the article.
Table of Comparison
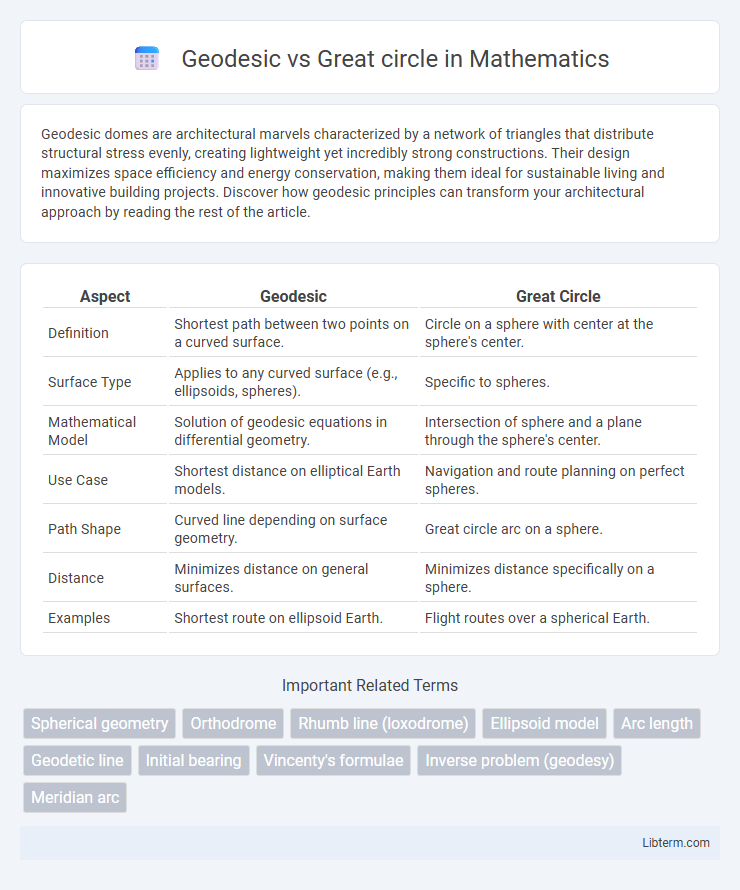
| Aspect | Geodesic | Great Circle |
|---|---|---|
| Definition | Shortest path between two points on a curved surface. | Circle on a sphere with center at the sphere's center. |
| Surface Type | Applies to any curved surface (e.g., ellipsoids, spheres). | Specific to spheres. |
| Mathematical Model | Solution of geodesic equations in differential geometry. | Intersection of sphere and a plane through the sphere's center. |
| Use Case | Shortest distance on elliptical Earth models. | Navigation and route planning on perfect spheres. |
| Path Shape | Curved line depending on surface geometry. | Great circle arc on a sphere. |
| Distance | Minimizes distance on general surfaces. | Minimizes distance specifically on a sphere. |
| Examples | Shortest route on ellipsoid Earth. | Flight routes over a spherical Earth. |
Understanding Geodesics and Great Circles
Geodesics represent the shortest path between two points on any curved surface, generalizing straight lines to curved spaces, while great circles specifically refer to the largest possible circles on a sphere, such as Earth, formed by the intersection of the sphere with a plane passing through its center. Great circles serve as practical geodesics on spherical surfaces, making them essential in navigation and aviation for determining the shortest travel distance. Understanding the distinction between geodesics as a mathematical concept and great circles as a specific application on spheres enhances precision in geospatial calculations and route planning.
Definitions: Geodesic vs Great Circle
A geodesic is the shortest path between two points on a curved surface, such as an ellipsoid, and can vary depending on the surface's geometry. A great circle is a specific type of geodesic that lies on a perfect sphere, representing the largest possible circle dividing the sphere into two equal hemispheres. While all great circles are geodesics on a sphere, geodesics on an ellipsoid are more complex and do not always coincide with great circles.
Mathematical Foundations
Geodesics represent the shortest path between two points on a curved surface, defined mathematically by the calculus of variations and differential geometry, often characterized by geodesic equations involving Christoffel symbols. Great circles, specifically on spheres, serve as geodesics where the path lies on the sphere's intersection with a plane passing through its center, described by spherical trigonometry and vector calculus. The mathematical distinction lies in geodesics applying to general curved manifolds whereas great circles are a specific case of geodesics on spherical surfaces, both essential in fields like geodesy, navigation, and differential geometry.
Geodesics on Different Surfaces
Geodesics represent the shortest paths between two points on curved surfaces, varying significantly depending on the surface geometry, such as spheres, ellipsoids, or hyperbolic planes. Unlike great circles, which are specific geodesics on spherical surfaces, geodesics adapt their curvature to the underlying surface metric, leading to unique shortest paths in non-spherical geometries. Understanding these geodesic properties is critical for applications in geospatial analysis, general relativity, and navigation systems on varied planetary bodies.
The Role of Great Circles on a Sphere
Great circles represent the shortest path between two points on a sphere, forming the foundation of geodesic calculations in spherical geometry. The role of great circles on a sphere is critical for navigation and mapping, as they define the minimal distance routes that aircraft and ships follow across the Earth's curved surface. Understanding great circles enables precise geodesic measurements essential for global positioning systems and geospatial analysis.
Applications in Navigation and Mapping
Great circle paths represent the shortest distance between two points on a sphere, making them essential for efficient air and sea navigation routes. Geodesics extend this concept to more complex surfaces such as ellipsoids, providing precise calculations for modern GPS and cartographic mapping systems. Accurate determination of geodesic routes enhances global positioning, route optimization, and spatial analysis in geographic information systems (GIS).
Differences in Distance Calculations
Geodesic distance represents the shortest path between two points on an ellipsoidal model of the Earth, accounting for its flattening and more precise shape. Great circle distance calculates the shortest path on a perfect sphere, often simplifying Earth's curvature, leading to slightly less accurate measurements. The geodesic method typically results in more precise distance calculations for navigation and mapping applications due to its consideration of Earth's ellipsoidal geometry.
Relevance in Geodesy and Cartography
Geodesic curves represent the shortest path between two points on a curved surface, essential for accurate distance measurements in geodesy, where Earth's ellipsoidal shape must be considered. Great circles are special cases of geodesics on a perfect sphere, widely used in cartography and navigation for plotting efficient routes over global maps. Precise geodesic calculations improve geospatial data accuracy, critical for mapping, surveying, and satellite positioning systems.
Practical Examples and Case Studies
Geodesic paths represent the shortest distance on curved surfaces, essential for accurate airline route planning by minimizing fuel consumption and travel time, while great circle routes approximate these paths on a spherical Earth model used in basic navigation systems. Case studies from shipping industries show geodesic calculations improving route efficiency in polar regions where great circle assumptions lead to significant deviations. Practical applications in GPS technology also rely on geodesic computations for precise location tracking over Earth's ellipsoidal shape.
Summary: Choosing the Right Path
Geodesic paths represent the shortest distance between two points on any curved surface, optimizing travel over complex terrains such as ellipsoidal models of Earth. Great circle routes provide a specific type of geodesic on a perfect sphere, commonly used in navigation and aviation for efficient long-distance travel. Selecting between geodesic and great circle calculations depends on the Earth model accuracy required, where geodesics yield more precise results on ellipsoidal surfaces compared to idealized great circles.
Geodesic Infographic
 libterm.com
libterm.com