Constant mean curvature surfaces exhibit a uniform average curvature at every point, balancing the surface's bending in various directions. These surfaces play a crucial role in differential geometry and appear in physical applications like soap films and bubbles due to their energy-minimizing properties. Explore the rest of the article to understand the mathematical foundations and real-world significance of constant mean curvature surfaces.
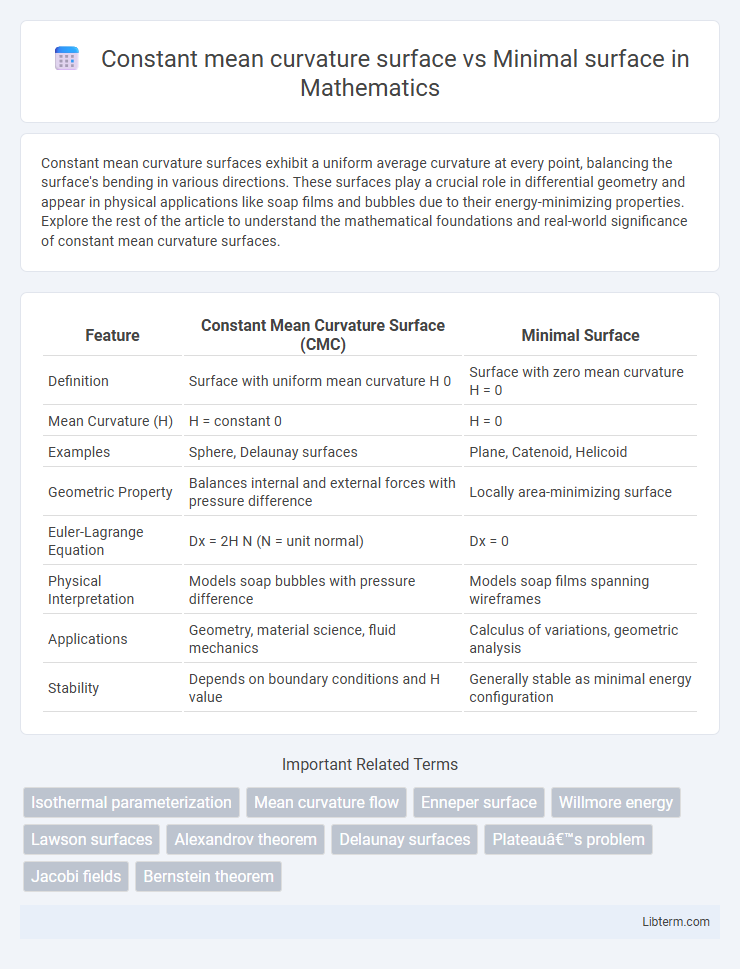
Table of Comparison
| Feature | Constant Mean Curvature Surface (CMC) | Minimal Surface |
|---|---|---|
| Definition | Surface with uniform mean curvature H 0 | Surface with zero mean curvature H = 0 |
| Mean Curvature (H) | H = constant 0 | H = 0 |
| Examples | Sphere, Delaunay surfaces | Plane, Catenoid, Helicoid |
| Geometric Property | Balances internal and external forces with pressure difference | Locally area-minimizing surface |
| Euler-Lagrange Equation | Dx = 2H N (N = unit normal) | Dx = 0 |
| Physical Interpretation | Models soap bubbles with pressure difference | Models soap films spanning wireframes |
| Applications | Geometry, material science, fluid mechanics | Calculus of variations, geometric analysis |
| Stability | Depends on boundary conditions and H value | Generally stable as minimal energy configuration |
Introduction to Surface Geometry
Constant mean curvature (CMC) surfaces exhibit uniform mean curvature at every point, making them critical models in studying equilibrium shapes under pressure constraints in surface geometry. Minimal surfaces, characterized by zero mean curvature, represent local area minimizers and serve as fundamental examples of surfaces with minimal energy configurations. The distinction between CMC and minimal surfaces lies in their curvature properties, with CMC surfaces including spheres and cylinders, while minimal surfaces encompass complex shapes like the catenoid and helicoid.
Understanding Constant Mean Curvature Surfaces
Constant mean curvature (CMC) surfaces are defined by having uniform mean curvature at every point, distinguishing them from minimal surfaces which have zero mean curvature. CMC surfaces generalize minimal surfaces by allowing a constant nonzero mean curvature, often leading to shapes like spheres and unduloids that model phenomena such as soap bubbles and biological membranes. Understanding these surfaces involves analyzing their geometric properties and stability, crucial for applications in differential geometry and physical sciences.
Defining Minimal Surfaces
Minimal surfaces are defined as surfaces with zero mean curvature at every point, representing critical points of the area functional under variations. Constant mean curvature (CMC) surfaces generalize minimal surfaces by having mean curvature equal to a nonzero constant, balancing surface tension with external pressure. The classic minimal surface examples include the catenoid and helicoid, while spheres exemplify non-minimal CMC surfaces.
Mathematical Formulation and Equations
Constant mean curvature (CMC) surfaces satisfy the equation H = constant, where H represents the mean curvature defined as the average of principal curvatures k1 and k2, specifically H = (k1 + k2)/2, leading to a nonlinear elliptic partial differential equation governing their shape. Minimal surfaces are a special case of CMC surfaces with mean curvature H = 0, characterized by the minimal surface equation div(grad u / sqrt(1 + |grad u|^2)) = 0, a nonlinear PDE derived from the vanishing mean curvature condition. Both surface types arise as critical points of area functional under constraints, with CMC surfaces corresponding to prescribed mean curvature conditions and minimal surfaces to area minimizers without volume constraint.
Key Differences Between CMC and Minimal Surfaces
Constant mean curvature (CMC) surfaces maintain a uniform mean curvature value at every point, often representing equilibrium shapes like soap bubbles under pressure. Minimal surfaces are a subset of CMC surfaces with zero mean curvature, characterized by minimal area and often modeled by soap films spanning wireframes. The key difference lies in the mean curvature value: CMC surfaces have constant but nonzero mean curvature, whereas minimal surfaces have exactly zero mean curvature, influencing their geometric properties and physical applications.
Geometric Properties and Visualization
Constant mean curvature (CMC) surfaces have mean curvature equal to a nonzero constant at every point, resulting in shapes like spheres or cylinders, whereas minimal surfaces feature zero mean curvature, leading to saddle-shaped or soap film-like geometries. Geometrically, CMC surfaces balance internal pressure forces, producing closed and stable configurations, while minimal surfaces minimize area locally, exhibiting intricate curvature patterns and often complex topologies. Visualization techniques highlight CMC surfaces with smooth, convex forms, contrasting with the highly curved, intricate folds characteristic of minimal surfaces in computer graphics and differential geometry.
Physical Examples and Applications
Constant mean curvature (CMC) surfaces appear in soap bubbles and liquid droplets, where surface tension balances pressure differences to maintain a fixed mean curvature. Minimal surfaces, characterized by zero mean curvature, model stable soap films spanning wireframes, minimizing surface area. Both surfaces are essential in material science and architecture for designing lightweight, stable structures and in biology to understand cellular membranes.
Stability and Variational Principles
Constant mean curvature (CMC) surfaces and minimal surfaces differ primarily in their stability properties and underlying variational principles. Minimal surfaces are critical points of the area functional with zero mean curvature and are stable under area-minimizing variations, often minimizing surface area locally. CMC surfaces, characterized by a constant but nonzero mean curvature, arise as critical points of the area functional with a volume constraint, exhibiting more complex stability behavior influenced by enclosed volume preservation.
Famous Surfaces: Classic Examples
Constant mean curvature surfaces, exemplified by the Delaunay surfaces such as nodoids and unduloids, exhibit a uniform mean curvature that differs from zero, often modeling soap bubbles and biological membranes under pressure. Minimal surfaces, including the iconic Enneper surface, Schwarz P surface, and Costa surface, possess zero mean curvature and represent equilibrium shapes minimizing area for a given boundary. These famous surfaces demonstrate fundamental differences in geometric properties and applications within differential geometry and materials science.
Future Directions and Research Challenges
Exploring future directions in constant mean curvature (CMC) surfaces versus minimal surfaces highlights challenges in understanding their stability under geometric flows and applicability in complex ambient spaces, such as curved manifolds or higher dimensions. Advances in numerical methods and variational techniques aim to characterize singularities and boundary behaviors unique to CMC surfaces compared to minimal surfaces. Research also focuses on integrating CMC surface theory with physical models in materials science and biology, addressing gaps in explicit classifications and computational simulations.
Constant mean curvature surface Infographic
 libterm.com
libterm.com