Analytic skills are essential for breaking down complex problems into manageable parts, enabling you to make informed decisions based on logical reasoning and data interpretation. Developing strong analytic abilities enhances problem-solving efficiency across various professional and personal scenarios. Explore the rest of the article to learn practical strategies for sharpening your analytic skills and applying them effectively.
Table of Comparison
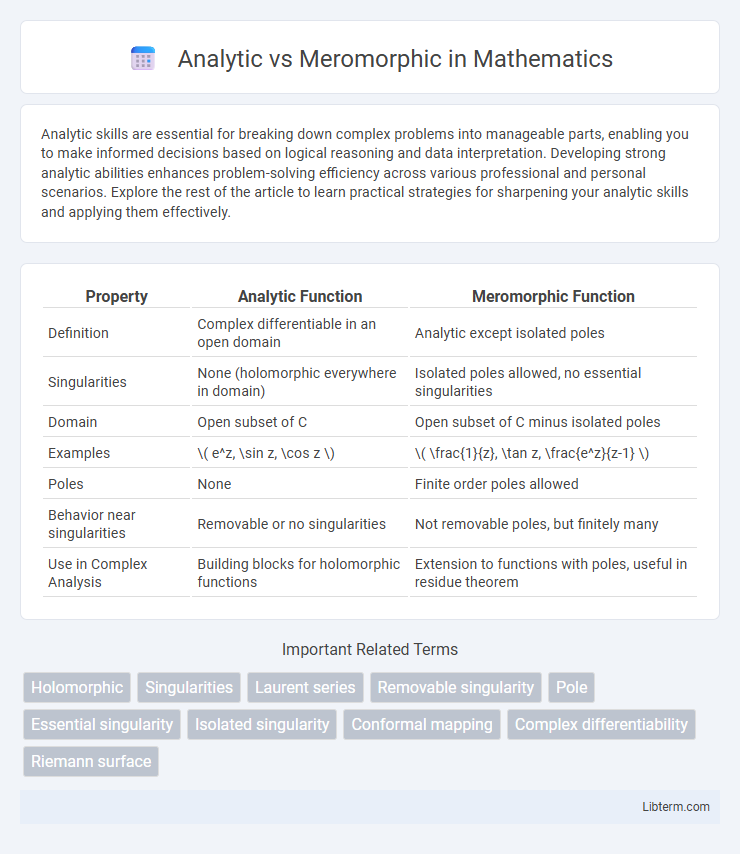
| Property | Analytic Function | Meromorphic Function |
|---|---|---|
| Definition | Complex differentiable in an open domain | Analytic except isolated poles |
| Singularities | None (holomorphic everywhere in domain) | Isolated poles allowed, no essential singularities |
| Domain | Open subset of C | Open subset of C minus isolated poles |
| Examples | \( e^z, \sin z, \cos z \) | \( \frac{1}{z}, \tan z, \frac{e^z}{z-1} \) |
| Poles | None | Finite order poles allowed |
| Behavior near singularities | Removable or no singularities | Not removable poles, but finitely many |
| Use in Complex Analysis | Building blocks for holomorphic functions | Extension to functions with poles, useful in residue theorem |
Understanding Analytic Functions
Analytic functions are complex functions that are locally represented by convergent power series, ensuring differentiability at every point within their domain. Unlike meromorphic functions that allow isolated poles (singularities) where the function may become infinite, analytic functions are holomorphic and free from such singularities in their region of definition. Understanding analytic functions involves recognizing their smooth, infinitely differentiable nature and their key role in complex analysis and conformal mappings.
Defining Meromorphic Functions
Meromorphic functions are complex functions that are analytic throughout their domain except for isolated poles, where they exhibit behavior like division by zero but without essential singularities. These poles are characterized as isolated singularities with a finite order, distinguishing meromorphic functions from purely analytic functions, which have no singularities. The concept is crucial in complex analysis because meromorphic functions can be expressed as the ratio of two analytic functions, expanding the scope of analytic continuation and residue theory.
Key Differences: Analytic vs Meromorphic
Analytic functions are complex functions that are differentiable at every point within their domain, exhibiting no singularities and maintaining smooth, continuous behavior. Meromorphic functions generalize analytic functions by allowing isolated poles, which are specific types of singularities where the function diverges to infinity, yet remain analytic elsewhere. The key difference lies in the presence of these poles: analytic functions have none, while meromorphic functions permit a finite number of isolated singularities within their domain.
Singularities in Analytic and Meromorphic Functions
Singularities in analytic functions are points where the function fails to be holomorphic, often characterized as isolated points with essential singularities or removable singularities. Meromorphic functions extend analytic functions by allowing poles, which are isolated singularities where the function diverges to infinity in a controlled manner. Understanding the classification of singularities--removable, poles, and essential--is crucial for analyzing the behavior and structure of meromorphic functions compared to purely analytic ones.
Domains of Analyticity and Meromorphicity
Analytic functions are complex functions that are differentiable at every point within an open domain, ensuring holomorphicity and local power series representation throughout the domain of analyticity. Meromorphic functions extend the concept by allowing isolated poles, which are singularities where the function tends to infinity, but remain analytic everywhere else within their domain of meromorphicity. The domain of analyticity is thus an open, pole-free region, whereas the domain of meromorphicity includes the analytic domain minus isolated poles, maintaining complex differentiability except at these singularities.
Common Examples and Applications
Analytic functions, such as polynomials and exponential functions, are differentiable everywhere in their domain and widely used in complex analysis and engineering for modeling continuous systems. Meromorphic functions, which include rational functions like \(\frac{1}{z}\) and the Gamma function, allow poles but no essential singularities, making them crucial in complex dynamics and number theory. Applications of analytic functions appear in signal processing and fluid dynamics, while meromorphic functions are essential in residue calculus and conformal mappings.
The Role of Poles and Essential Singularities
Poles in meromorphic functions represent isolated singularities where the function approaches infinity, allowing for residue calculation critical in complex analysis and contour integration. Analytic functions are free of such singularities within their domain, maintaining differentiability and power series expansions everywhere except at points of essential singularities or poles if extended. Essential singularities exhibit highly intricate behavior, with functions neither bounded nor approaching infinity, producing wild oscillations that defy traditional classification seen in analytic or meromorphic functions.
Analytic Continuation and its Limits
Analytic continuation extends the domain of an analytic function beyond its radius of convergence by connecting power series expansions through overlapping regions, preserving holomorphic properties. However, this continuation may encounter natural boundaries or singularities, such as poles or essential singularities, where the function ceases to be meromorphic or analytic. Understanding these limits is crucial for distinguishing analytic functions that can be globally continued from meromorphic functions characterized by isolated poles within their maximal domains.
Meromorphic Functions in Complex Analysis
Meromorphic functions in complex analysis are functions that are analytic except at isolated poles, where they exhibit defined types of singularities but no essential singularities or branch points. These functions can be expressed as a quotient of two analytic functions, allowing for a well-understood extension of analytic function theory with pole behavior characterized by principal parts in their Laurent series expansions. Meromorphic functions play a critical role in complex dynamics, residue theory, and the classification of singularities, providing a framework for studying functions with controlled singularities in the complex plane.
Choosing Between Analytic and Meromorphic Models
Choosing between analytic and meromorphic models depends on the nature of the functions involved and the desired properties in complex analysis. Analytic models are ideal for studying functions that are holomorphic everywhere in a domain, ensuring smoothness and differentiability without singularities. Meromorphic models extend analytic ones by allowing isolated poles, making them essential for analyzing functions with well-defined singularities and complex residues.
Analytic Infographic
 libterm.com
libterm.com