An ordered ring is an algebraic structure equipped with a ring and a compatible total order that respects addition and multiplication. This means the order preserves the ring operations, allowing comparisons of elements while maintaining algebraic properties. Explore the rest of the article to understand how ordered rings influence various mathematical theories and applications.
Table of Comparison
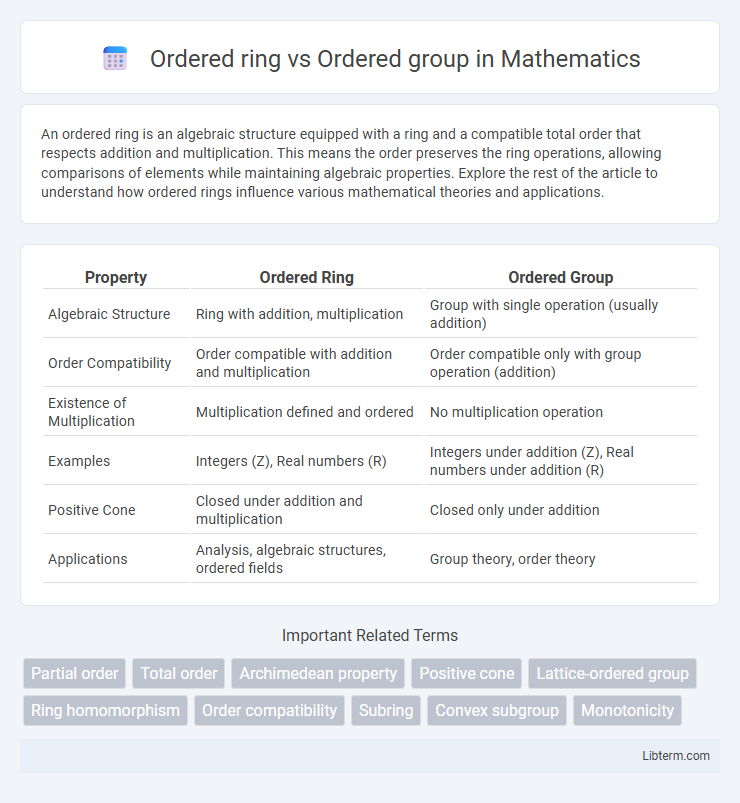
| Property | Ordered Ring | Ordered Group |
|---|---|---|
| Algebraic Structure | Ring with addition, multiplication | Group with single operation (usually addition) |
| Order Compatibility | Order compatible with addition and multiplication | Order compatible only with group operation (addition) |
| Existence of Multiplication | Multiplication defined and ordered | No multiplication operation |
| Examples | Integers (Z), Real numbers (R) | Integers under addition (Z), Real numbers under addition (R) |
| Positive Cone | Closed under addition and multiplication | Closed only under addition |
| Applications | Analysis, algebraic structures, ordered fields | Group theory, order theory |
Introduction to Ordered Rings and Ordered Groups
Ordered rings extend ordered groups by incorporating both additive and multiplicative operations under a compatible total order, where the set is equipped with an order relation that respects addition and multiplication. Ordered groups consist solely of a group structure with a total order compatible with the group operation, emphasizing order preservation under addition without involving multiplication. The key distinction lies in ordered rings requiring multiplicative compatibility with the order, enabling richer algebraic and order-theoretic properties crucial in real algebraic geometry and valuation theory.
Definition of Ordered Group
An ordered group is a group G equipped with a total order <= that is translation-invariant, meaning for all a, b, c in G, if a <= b then ac <= bc and ca <= cb. Unlike ordered rings, which have both additive and multiplicative structures compatible with their order, ordered groups focus solely on the group operation and its interaction with the order. This property ensures the group's algebraic structure harmonizes with its order, making ordered groups integral in areas like algebraic topology and ordered algebraic systems.
Definition of Ordered Ring
An ordered ring is a ring equipped with a total order compatible with ring operations, meaning if a <= b then a + c <= b + c and 0 <= a, 0 <= b imply 0 <= ab. In contrast, an ordered group only requires a compatible order with the group operation, lacking multiplicative structure. Ordered rings extend ordered groups by incorporating multiplication while preserving order properties, crucial in algebraic structures like fields of real numbers.
Key Differences Between Ordered Rings and Ordered Groups
Ordered rings are algebraic structures equipped with both a total order and compatible ring operations of addition and multiplication, while ordered groups feature a total order compatible only with the group operation of addition. A key difference lies in the presence of multiplication in ordered rings, enabling notions like positivity to be extended multiplicatively, which is absent in ordered groups. Furthermore, ordered rings must satisfy order-preserving properties for multiplication, whereas ordered groups focus solely on translation invariance under addition.
Algebraic Properties of Ordered Groups
Ordered groups exhibit a total order compatible with the group operation, meaning for any elements a, b, and c, if a <= b then ac <= bc and ca <= cb, preserving algebraic structure under multiplication. Unlike ordered rings, ordered groups do not necessarily have distributivity or additive and multiplicative identity distinctness, focusing instead on the order's interaction with group operation. Key algebraic properties include the existence of positive cones that are closed under the group operation and contain no inverses except the identity, enabling the order to reflect the group's algebraic structure.
Algebraic Properties of Ordered Rings
Ordered rings extend the concept of ordered groups by incorporating both additive and multiplicative structures, requiring the ring to have a total order compatible with addition and multiplication. The positive cone in an ordered ring is closed under addition and multiplication, ensuring the product of two positive elements remains positive, a property not present in ordered groups. Key algebraic properties include closure under multiplication, distributivity, and the preservation of order under addition, which collectively distinguish ordered rings from ordered groups in algebraic theory.
Examples of Ordered Groups
Ordered groups include examples such as the set of integers \((\mathbb{Z}, +)\) with the usual order, where addition and order are compatible, and the additive group of real numbers \((\mathbb{R}, +)\) with the standard less-than relation. In contrast, ordered rings extend ordered groups by including a compatible multiplication operation, as seen in the ordered ring of integers \(\mathbb{Z}\) with standard addition, multiplication, and order. Ordered groups emphasize the interplay between group operations and ordering, making the integers and real numbers prime examples of ordered groups used in algebra and analysis.
Examples of Ordered Rings
Ordered rings, such as the ring of integers \(\mathbb{Z}\) with the standard order, serve as fundamental examples where addition and multiplication preserve order. The ring of polynomials with real coefficients, \(\mathbb{R}[x]\), ordered by evaluating polynomials at a fixed point, illustrates an ordered ring structure with applications in real algebraic geometry. Unlike ordered groups, ordered rings require compatibility of multiplication with the order, making examples like \(\mathbb{Z}\) and \(\mathbb{R}[x]\) essential for understanding ordered algebraic systems.
Applications of Ordered Rings and Ordered Groups
Ordered rings are fundamental in real algebraic geometry and number theory, where their structure enables the study of polynomial inequalities and solution sets. Ordered groups appear prominently in dynamical systems and economics, providing an algebraic framework for ordered data like time or resource allocation. Both ordered rings and groups are instrumental in optimization theory, particularly in defining monotone operators and ordered vector spaces for problem-solving.
Summary: Choosing Between an Ordered Ring and an Ordered Group
Ordered rings extend ordered groups by incorporating both additive and multiplicative structures compatible with the order, allowing for richer algebraic operations and properties. When the presence of a multiplicative identity and closure under multiplication are essential, ordered rings provide a more suitable framework than ordered groups, which only require an additive group structure with a translation-invariant order. Selecting between an ordered ring and an ordered group depends on whether multiplication and ring axioms must coexist harmoniously with the order, influencing applications in ordered algebraic systems and real algebraic geometry.
Ordered ring Infographic
 libterm.com
libterm.com