Co-NP is a complexity class containing decision problems whose complements are in NP, meaning they can be verified efficiently if given a "no" instance. Understanding co-NP is critical for exploring the relationship between NP and its complementary problems, which impacts computational theory and algorithm design. Discover how co-NP influences complexity theory and what it means for your problem-solving strategies in the full article.
Table of Comparison
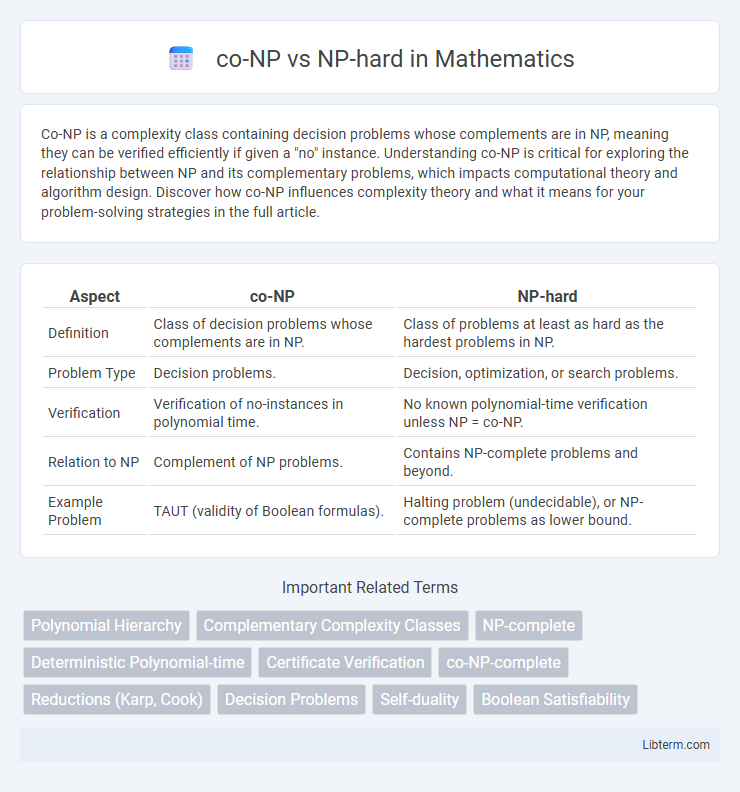
| Aspect | co-NP | NP-hard |
|---|---|---|
| Definition | Class of decision problems whose complements are in NP. | Class of problems at least as hard as the hardest problems in NP. |
| Problem Type | Decision problems. | Decision, optimization, or search problems. |
| Verification | Verification of no-instances in polynomial time. | No known polynomial-time verification unless NP = co-NP. |
| Relation to NP | Complement of NP problems. | Contains NP-complete problems and beyond. |
| Example Problem | TAUT (validity of Boolean formulas). | Halting problem (undecidable), or NP-complete problems as lower bound. |
Introduction to Computational Complexity
Co-NP represents the class of decision problems where the complement problem is in NP, meaning that for "no" instances, a proof can be verified efficiently by a nondeterministic polynomial-time algorithm. NP-hard problems are at least as hard as the hardest problems in NP, encompassing all problems for which no polynomial-time algorithm is known and whose solutions cannot be efficiently verified. Understanding the distinction between co-NP and NP-hard within computational complexity theory is essential for classifying problems based on their computational difficulty and verifying solution proofs.
Defining co-NP: Concepts and Examples
co-NP consists of decision problems for which the no-instances can be verified efficiently by a nondeterministic polynomial-time algorithm, serving as the complement class to NP. A canonical example is the tautology problem, where determining if a Boolean formula is always true lies in co-NP since non-tautologies can be efficiently verified by providing a counterexample. Understanding co-NP requires analyzing these complement verification processes and their relations to NP-hard problems known for their computational intractability.
Understanding NP-hard Problems
NP-hard problems represent a class of computational challenges that are at least as difficult as the hardest problems in NP, with no known polynomial-time solutions. Understanding NP-hard problems involves recognizing their role in computational complexity, where they serve as benchmarks for the limits of efficient algorithm design. These problems often arise in optimization, decision-making, and logic, highlighting the significant challenges in verifying solutions quickly compared to NP or co-NP classifications.
Key Differences Between co-NP and NP-hard
co-NP consists of decision problems whose complements are in NP, primarily characterized by verification of "no" instances in polynomial time, whereas NP-hard represents problems at least as hard as the hardest problems in NP without requiring solutions to be in NP themselves. co-NP problems often deal with universal quantification, contrasting with the existential quantification typical in NP, while NP-hard problems may not be decidable or verifiable within polynomial time. The key difference lies in co-NP's focus on complement problem verification versus NP-hard's role as a complexity class encompassing the most computationally challenging problems that influence both NP and beyond.
Relationship Between NP, NP-complete, NP-hard, and co-NP
NP problems are decision problems verifiable in polynomial time, while co-NP consists of problems whose complements are in NP. NP-complete problems represent the intersection of NP and NP-hard, meaning they are the hardest problems in NP and, if solved efficiently, would solve all NP problems. The relationship between NP-hard and co-NP highlights that NP-hard problems are at least as hard as the hardest problems in NP, but they may not belong to NP or co-NP, creating a complex interplay in computational complexity theory.
Real-world Examples of co-NP and NP-hard Problems
Co-NP problems include verifying that a number is not prime, such as primality testing's complement, where proofs of compositeness serve as certificates. NP-hard problems encompass optimization challenges like the Traveling Salesman Problem and scheduling tasks, where finding the shortest route or optimal schedule cannot be done efficiently. Real-world applications of co-NP relate to security protocol validation, while NP-hard problems are prevalent in logistics, circuit design, and resource allocation.
Common Misconceptions about co-NP and NP-hard
Common misconceptions about co-NP and NP-hard often confuse their definitions and relationships; co-NP is the class containing decision problems whose complements are in NP, while NP-hard includes problems at least as hard as the hardest problems in NP but may not be in NP or co-NP. Many incorrectly assume co-NP problems are simply the complements of NP-hard problems, but NP-hardness addresses computational difficulty and not membership in a complexity class. Understanding that NP-hard problems can be undecidable or outside NP/co-NP clarifies the distinction and corrects the widespread confusion regarding their computational properties.
Importance in Theoretical Computer Science
The distinction between co-NP and NP-hard classes plays a crucial role in theoretical computer science by helping researchers understand the complexity boundaries of decision problems. co-NP contains decision problems whose complements are in NP, highlighting the dual nature of problem verification, while NP-hard encompasses problems at least as hard as the hardest problems in NP, often indicating intractability. This classification informs algorithm design, complexity theory, and computational feasibility, guiding the search for efficient solutions or proving their non-existence.
Open Questions and Research Directions
The relationship between co-NP and NP-hard remains a fundamental open question in computational complexity theory, specifically whether co-NP is contained within NP-hard or if they are distinct classes. Research continues to explore reductions and completeness results to better characterize co-NP problems in terms of their hardness and solvability, with significant implications for the P vs NP problem. Investigating structural properties of co-NP and novel algorithmic approaches aims to uncover potential collapses or separations within the polynomial hierarchy, shaping future advancements in complexity theory.
Conclusion: Implications for Complexity Theory
Co-NP and NP-hard classes highlight the nuanced landscape of computational complexity, where problems in co-NP are complements of NP problems while NP-hard includes challenges at least as difficult as the hardest NP problems. The distinction underscores that demonstrating a problem is co-NP complete or NP-hard has profound theoretical consequences, influencing our understanding of P versus NP and the boundaries of efficient computability. These implications drive ongoing research into algorithm design and complexity class separations, shaping fundamental questions in computational theory.
co-NP Infographic
 libterm.com
libterm.com