A simply connected space is a key concept in topology, defined as a space without any holes, where every loop can be continuously contracted to a single point. This property plays a crucial role in fields like complex analysis and algebraic topology, influencing how functions behave and shapes relate. Discover how understanding simply connected spaces can deepen your insight into mathematical structures by exploring the full article.
Table of Comparison
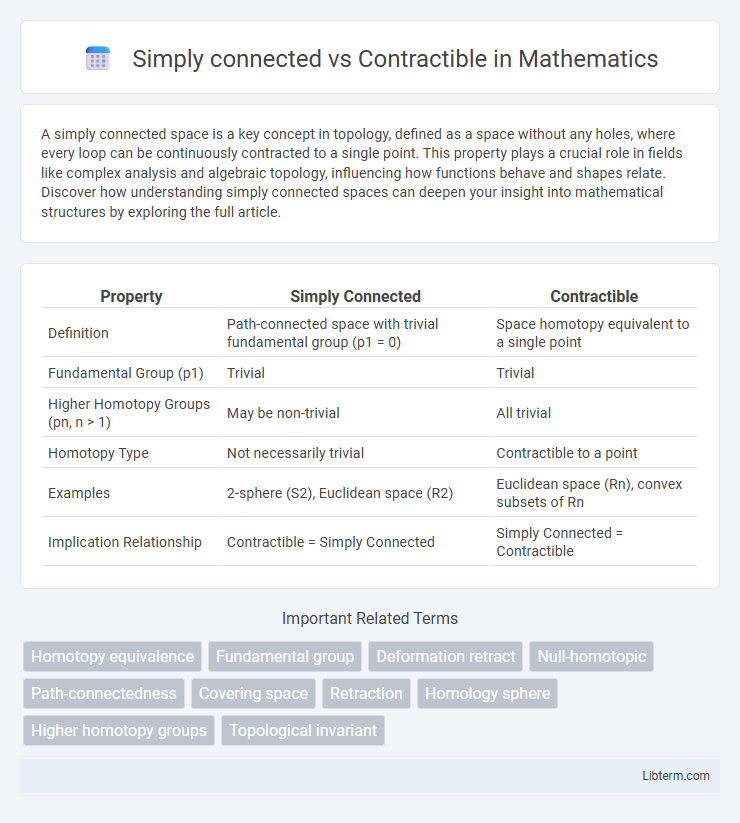
| Property | Simply Connected | Contractible |
|---|---|---|
| Definition | Path-connected space with trivial fundamental group (p1 = 0) | Space homotopy equivalent to a single point |
| Fundamental Group (p1) | Trivial | Trivial |
| Higher Homotopy Groups (pn, n > 1) | May be non-trivial | All trivial |
| Homotopy Type | Not necessarily trivial | Contractible to a point |
| Examples | 2-sphere (S2), Euclidean space (R2) | Euclidean space (Rn), convex subsets of Rn |
| Implication Relationship | Contractible = Simply Connected | Simply Connected = Contractible |
Introduction to Topological Spaces
Simply connected spaces are topological spaces without holes, meaning every loop can be continuously contracted to a single point, which directly relates to the fundamental group being trivial. Contractible spaces are even stronger; they can be continuously shrunk to a point within the space itself, indicating they are homotopy equivalent to a single point and thus simply connected. Understanding these concepts is essential in topology for classifying spaces based on their shape and connectivity properties.
Defining Simply Connected Spaces
Simply connected spaces are topological spaces that are path-connected and have a trivial fundamental group, meaning every loop can be continuously contracted to a point within the space. Contractible spaces are a stronger concept, where the space itself can be continuously shrunk to a single point, implying it is simply connected but not all simply connected spaces are contractible. Understanding the difference hinges on the homotopy properties: simply connected spaces require trivial loops, while contractible spaces require the existence of a homotopy equivalence to a point.
Understanding Contractible Spaces
Contractible spaces are those that can be continuously shrunk to a point within the space, meaning they have trivial homotopy groups at all levels. Unlike simply connected spaces, which require only the fundamental group to be trivial, contractible spaces have stronger topological properties, ensuring all higher homotopy groups vanish as well. This strong form of "shrinkability" implies that contractible spaces are topologically equivalent to a single point, making them important in homotopy theory and algebraic topology.
Key Differences Between Simply Connected and Contractible
Simply connected spaces have a single, unbreakable loop structure where every loop can be continuously contracted to a point, but they may have complex higher-dimensional holes. Contractible spaces are stronger topologically, being homotopy equivalent to a point, ensuring all homotopy groups vanish and the space can be continuously shrunk to a point without leaving the space. The key difference lies in contractibility implying simple connectivity, while simple connectivity does not guarantee contractibility due to potential higher-dimensional topological features.
Algebraic Topology: Fundamental Group Perspective
Simply connected spaces have a trivial fundamental group, indicating every loop can be continuously contracted to a point, while contractible spaces are homotopy equivalent to a single point, ensuring all higher homotopy groups vanish. The contractibility implies simple connectivity, but the converse is not necessarily true, highlighting that simply connected spaces may have nontrivial higher homotopy groups. From the fundamental group perspective in algebraic topology, the distinction emphasizes that triviality of p1 is a necessary but not sufficient condition for contractibility.
Examples of Simply Connected but Non-Contractible Spaces
The 2-dimensional sphere \( S^2 \) serves as a classic example of a simply connected but non-contractible space, as every loop can be continuously contracted to a point yet the space itself cannot be shrunk to a single point without leaving the sphere. Similarly, complex projective spaces \( \mathbb{CP}^n \) for \( n \geq 1 \) are simply connected but exhibit rich topological structure preventing contractibility. These spaces highlight the distinction that simple connectivity ensures the triviality of the fundamental group \(\pi_1\), while contractibility requires all higher homotopy groups \(\pi_n\) to vanish as well.
Examples of Contractible Spaces
Contractible spaces include Euclidean spaces \(\mathbb{R}^n\), where any point can be continuously shrunk to a single point within the space. Examples also encompass convex subsets of \(\mathbb{R}^n\), such as disks, balls, and star-shaped regions, all of which are contractible due to their ability to deform to a point without leaving the space. Unlike simply connected spaces that require trivial fundamental groups, contractible spaces exhibit stronger properties by being homotopy equivalent to a single point, ensuring both trivial fundamental groups and higher homotopy groups.
Visualizing the Concepts: Intuitive Analogies
Simply connected spaces resemble a smooth rubber sheet with no holes, allowing any loop to shrink to a point without tearing. Contractible spaces take this further, acting like a deflatable balloon that can collapse completely to a single point within the space itself. Visualizing simply connected spaces as donut-free surfaces and contractible spaces as those reducible to a point captures their fundamental topological differences clearly.
Applications in Mathematics and Physics
Simply connected spaces, characterized by having no non-contractible loops, play a crucial role in complex analysis, differential geometry, and gauge theory by ensuring unique solutions to certain differential equations and simplifying topological classification. Contractible spaces, being homotopy equivalent to a point, are fundamental in homotopy theory and algebraic topology, providing trivial higher homotopy groups that aid in simplifying computations of topological invariants. In physics, simply connected manifolds are essential in the study of magnetic monopoles and quantum field theories, while contractible spaces often model spacetime regions with trivial topology, influencing theories of general relativity and quantum gravity.
Summary and Implications
Simply connected spaces have no holes and every loop can be continuously contracted to a point, indicating a trivial fundamental group. Contractible spaces are stronger, as they can be continuously shrunk to a single point, implying simple connectivity but not vice versa. Understanding this distinction is crucial in topology since contractibility guarantees homotopy equivalence to a point, impacting the classification of spaces and their topological invariants.
Simply connected Infographic
 libterm.com
libterm.com