Branch and Bound is an effective algorithmic method used to solve complex optimization problems by systematically exploring and pruning branches in a search tree. This technique significantly reduces computation time by eliminating paths that cannot yield better solutions than already found ones. Discover how Branch and Bound can optimize your problem-solving approach by reading the rest of this article.
Table of Comparison
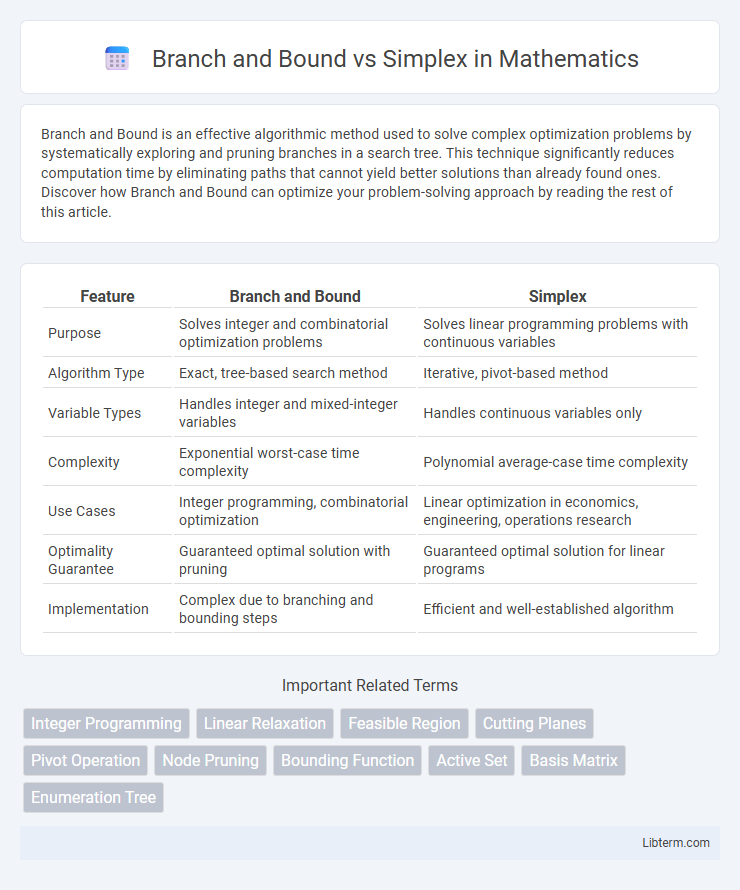
| Feature | Branch and Bound | Simplex |
|---|---|---|
| Purpose | Solves integer and combinatorial optimization problems | Solves linear programming problems with continuous variables |
| Algorithm Type | Exact, tree-based search method | Iterative, pivot-based method |
| Variable Types | Handles integer and mixed-integer variables | Handles continuous variables only |
| Complexity | Exponential worst-case time complexity | Polynomial average-case time complexity |
| Use Cases | Integer programming, combinatorial optimization | Linear optimization in economics, engineering, operations research |
| Optimality Guarantee | Guaranteed optimal solution with pruning | Guaranteed optimal solution for linear programs |
| Implementation | Complex due to branching and bounding steps | Efficient and well-established algorithm |
Introduction to Branch and Bound and Simplex
Branch and Bound is an algorithmic method primarily used for solving integer programming problems by systematically exploring and pruning the solution space to find optimal solutions. Simplex, on the other hand, is an efficient linear programming technique that navigates the vertices of the feasible region to optimize linear objective functions. Both methods address optimization but differ in application domains, with Branch and Bound targeting combinatorial problems and Simplex focused on continuous linear constraints.
Fundamental Principles of the Simplex Method
The Simplex Method operates by traversing the vertices of the feasible region defined by linear constraints to find the optimal value of a linear programming problem, employing pivot operations to move towards improved solutions iteratively. Branch and Bound, in contrast, addresses integer programming problems by systematically partitioning the solution space into smaller subsets, bounding their potential to contain optimal solutions without enumerating all possibilities. The fundamental principle of the Simplex method lies in its efficient navigation of the convex polytope's edges to optimize the objective function, leveraging algebraic operations on the tableau to update basic feasible solutions.
Core Concepts of the Branch and Bound Technique
Branch and Bound is a combinatorial optimization algorithm that systematically explores decision tree nodes, using upper and lower bounds to prune suboptimal branches, thus reducing the search space. It relies on bounding functions derived from problem relaxations, such as linear programming relaxations solved by the Simplex method, to estimate node quality efficiently. Core concepts include node selection strategies, bounding, and branching rules, which together ensure convergence to the global optimum in integer and combinatorial problems.
Key Differences Between Branch and Bound and Simplex
Branch and Bound is a combinatorial optimization algorithm designed for integer programming problems, while Simplex is a linear programming method that solves continuous optimization problems. Branch and Bound systematically explores feasible solutions by partitioning the search space and pruning suboptimal branches, whereas Simplex navigates the vertices of the feasible region's polytope to find the optimal solution efficiently. The key difference lies in Branch and Bound's capability to handle discrete variables and integrality constraints, which Simplex cannot directly address.
Practical Applications of the Simplex Method
The Simplex method is widely used in practical applications such as linear programming for optimizing resource allocation in industries like manufacturing, transportation, and finance. It efficiently solves problems involving constraints and objective functions by navigating vertices of feasible regions to find optimal solutions. Compared to Branch and Bound, which tackles integer and combinatorial optimization by systematically exploring solution spaces, the Simplex method excels in continuous linear optimization problems with established efficiency and scalability.
Use Cases for Branch and Bound in Optimization
Branch and Bound is primarily used in integer programming and combinatorial optimization problems where variables are discrete, such as scheduling, vehicle routing, and knapsack problems. Unlike the Simplex method, which efficiently solves linear programming problems with continuous variables, Branch and Bound systematically explores feasible solutions by dividing the problem into subproblems, pruning branches that cannot yield better solutions. This method excels in tackling combinatorial explosion and finding global optima in NP-hard problems where exact solutions are critical.
Computational Complexity: Branch and Bound vs Simplex
Branch and Bound algorithms exhibit exponential time complexity in the worst case due to exhaustive search over feasible regions, making them computationally intensive for large-scale integer programming problems. The Simplex method, while having exponential worst-case complexity, performs efficiently on most practical linear programming instances with polynomial average-case behavior. Branch and Bound is preferred for combinatorial optimization requiring integer solutions, whereas Simplex excels in continuous linear programming due to its computational efficiency.
Strengths and Limitations of Each Approach
Branch and Bound excels in solving integer programming problems by systematically exploring feasible solutions and pruning suboptimal branches, making it highly effective for combinatorial optimization but often computationally intensive for large-scale problems. The Simplex method efficiently handles linear programming problems by navigating vertices of the feasible region to find optimal solutions quickly, yet struggles with integer constraints and can cycle without improvements. While Branch and Bound ensures global optimality for discrete variables, Simplex offers rapid convergence for continuous variables but requires extensions like cutting planes or branch-and-cut to address integer programming challenges.
Choosing the Right Algorithm: Branch and Bound or Simplex?
Choosing the right algorithm depends on the problem type: Branch and Bound is ideal for integer programming problems requiring discrete solutions, while Simplex excels in solving continuous linear programming problems efficiently. Branch and Bound systematically explores feasible solution spaces by partitioning and pruning, suitable for combinatorial cases, whereas Simplex navigates the vertices of convex polyhedra to find optimal values in polynomial time. Evaluating problem constraints and solution requirements ensures selection of the algorithm that balances computational complexity and solution precision.
Future Trends in Optimization Algorithms
Future trends in optimization algorithms emphasize hybrid approaches combining Branch and Bound with the Simplex method to exploit their complementary strengths in solving mixed-integer and linear programming problems efficiently. Advancements in machine learning integration aim to predict optimal branching decisions and pivot selections, significantly reducing computational time. Quantum computing and parallel processing further promise to revolutionize these techniques by enabling faster exploration of solution spaces and enhanced scalability for complex optimization models.
Branch and Bound Infographic
 libterm.com
libterm.com