A Teichmuller map is a quasiconformal homeomorphism between Riemann surfaces that minimizes distortion and preserves complex structures in an optimal way. It plays a vital role in Teichmuller theory and the study of moduli spaces, offering insights into geometric structures and deformation spaces. Explore the rest of the article to understand how these maps influence complex analysis and geometric topology.
Table of Comparison
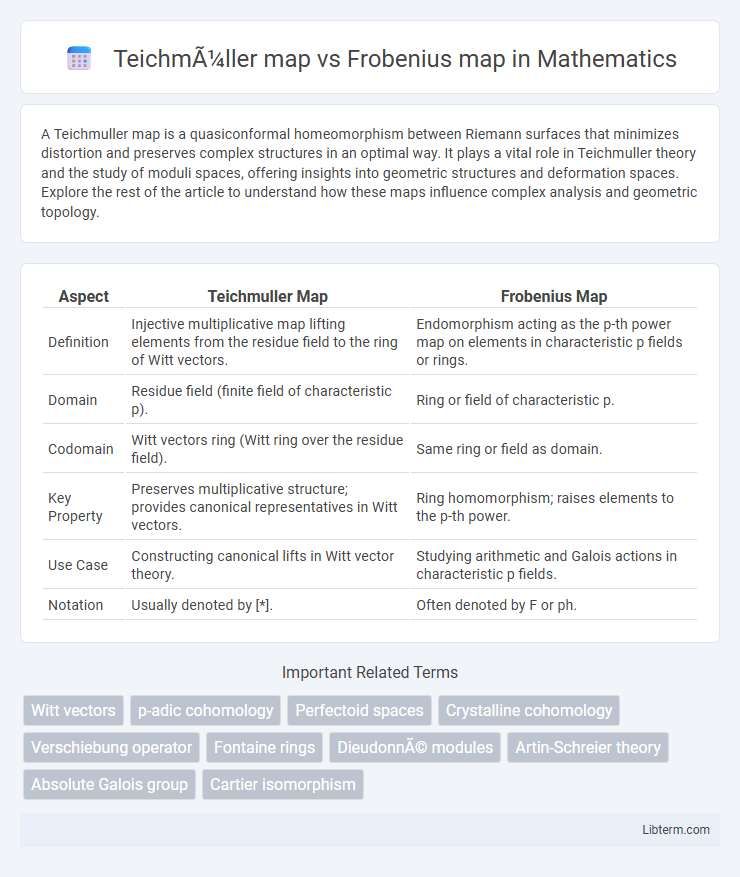
| Aspect | Teichmuller Map | Frobenius Map |
|---|---|---|
| Definition | Injective multiplicative map lifting elements from the residue field to the ring of Witt vectors. | Endomorphism acting as the p-th power map on elements in characteristic p fields or rings. |
| Domain | Residue field (finite field of characteristic p). | Ring or field of characteristic p. |
| Codomain | Witt vectors ring (Witt ring over the residue field). | Same ring or field as domain. |
| Key Property | Preserves multiplicative structure; provides canonical representatives in Witt vectors. | Ring homomorphism; raises elements to the p-th power. |
| Use Case | Constructing canonical lifts in Witt vector theory. | Studying arithmetic and Galois actions in characteristic p fields. |
| Notation | Usually denoted by [*]. | Often denoted by F or ph. |
Introduction to Teichmüller and Frobenius Maps
Teichmuller maps provide canonical representatives of elements in finite fields as roots of unity in their unramified extensions, playing a crucial role in p-adic number theory and Witt vector construction. Frobenius maps act as field automorphisms raising elements to the p-th power in characteristic p fields, fundamental to arithmetic geometry and algebraic geometry over finite fields. Both maps connect deeply through their interaction in lifting and understanding arithmetic properties in fields of positive characteristic.
Historical Context and Development
The Teichmuller map originated in the early 20th century through Oswald Teichmuller's work on quasiconformal mappings and complex analysis, laying foundations for modern Teichmuller theory. The Frobenius map, named after Ferdinand Frobenius, emerged in the late 19th century as a key tool in algebra and number theory, particularly in the study of finite fields and algebraic geometry. Both maps have since played crucial roles in arithmetic geometry and the development of p-adic Hodge theory, intertwining their historical trajectories within the broader context of algebraic and analytic structures.
Formal Definitions
The Teichmuller map is a canonical embedding from the residue field of a complete discrete valuation ring with perfect residue field into its ring of Witt vectors, defined by lifting each element to a unique Witt vector fixed by Frobenius. The Frobenius map is a ring endomorphism on Witt vectors over a field of characteristic p, raising each Witt component to its p-th power and shifting indices in the Witt vector coordinates. Formally, the Teichmuller map t: k - W(k) satisfies t(a) = (a, 0, 0, ...) with Frobenius ph acting as ph((a_0, a_1, ...)) = (a_0^p, a_1^p, ...).
Algebraic Structures Involved
The Teichmuller map is a multiplicative section from a finite field of characteristic p to its ring of Witt vectors, preserving the algebraic structure by embedding field elements into a characteristic zero ring. The Frobenius map, defined on rings of characteristic p, raises each element to its p-th power and acts as an endomorphism preserving the ring structure but altering additive properties. Together, these maps play crucial roles in the study of Witt vectors and algebraic geometry, connecting finite field arithmetic with p-adic and characteristic zero algebraic frameworks.
Teichmüller Map: Properties and Applications
The Teichmuller map is a canonical lift from a finite field \(\mathbb{F}_p\) to its ring of Witt vectors \(W(\mathbb{F}_p)\), preserving multiplicative structures and providing a unique representative for each residue class modulo \(p\). It is a multiplicative section of the reduction map and is crucial for defining coordinates in the Witt vector framework, enabling explicit calculations in \(p\)-adic Hodge theory and deformation theory. Applications include simplifying the structure of perfectoid fields, constructing Frobenius splittings, and facilitating arithmetic geometry computations through precise control over lifting operations.
Frobenius Map: Properties and Applications
The Frobenius map, a fundamental endomorphism in fields of characteristic p, raises each element to its p-th power and preserves the field structure, making it a crucial tool in algebraic geometry and number theory. It is a key component in the study of finite fields, enabling the classification of field extensions and playing a central role in the theory of Galois representations and etale cohomology. The map's properties facilitate the understanding of the arithmetic of varieties over finite fields, contributing to advances in cryptography, error-correcting codes, and the proof of the Weil conjectures.
Comparative Analysis: Teichmüller vs Frobenius Maps
The Teichmuller map embeds elements from a finite field into its ring of Witt vectors, preserving multiplicative structure and providing unique canonical representatives. In contrast, the Frobenius map acts as an endomorphism, raising each element to its p-th power, and plays a fundamental role in field extensions and Galois theory. While the Teichmuller map facilitates lifting and computations in characteristic zero, the Frobenius map governs arithmetic dynamics in characteristic p, making their interplay essential in p-adic Hodge theory and arithmetic geometry.
Roles in Number Theory and Arithmetic Geometry
The Teichmuller map provides a canonical embedding of a finite field into its Witt ring, enabling the study of liftings of field elements and facilitating explicit computations in p-adic Hodge theory. The Frobenius map, as an endomorphism acting on algebraic varieties over fields of positive characteristic, plays a central role in understanding arithmetic properties through fixed points and eigenvalues, crucial for the formulation of the Weil conjectures. In arithmetic geometry, the interplay between the Frobenius morphism and the Teichmuller representatives supports the analysis of Galois representations and crystalline cohomology, linking number-theoretic phenomena with geometric structures.
Examples and Computational Aspects
The Teichmuller map is commonly illustrated in the context of finite fields, where each element is uniquely represented as a root of unity in characteristic p, facilitating explicit computations in the ring of Witt vectors. In contrast, the Frobenius map acts as a field automorphism raising elements to the p-th power, with computational efficiency arising from its simple algebraic form, especially in finite fields and schemes over characteristic p. Both maps play crucial roles in computational number theory and algebraic geometry; the Teichmuller map is valuable for lifting elements from residue fields while the Frobenius map enables fast exponentiation and structure-preserving transformations.
Conclusion and Future Directions
The Teichmuller map and Frobenius map serve distinct roles in p-adic number theory, with the former providing a canonical lift from finite fields to Witt vectors and the latter acting as a fundamental endomorphism in characteristic p settings. Advances in understanding their interplay promise enhancements in computational algorithms for arithmetic geometry and cryptography. Future research may focus on exploiting these maps for novel applications in p-adic Hodge theory and improving explicit descriptions of Galois representations.
Teichmüller map Infographic
 libterm.com
libterm.com