A simple group is a fundamental concept in abstract algebra, defined as a nontrivial group whose only normal subgroups are the trivial group and the group itself. These groups serve as the building blocks for all finite groups, much like prime numbers do for integers. Explore the rest of this article to understand how simple groups play a crucial role in the classification of finite groups.
Table of Comparison
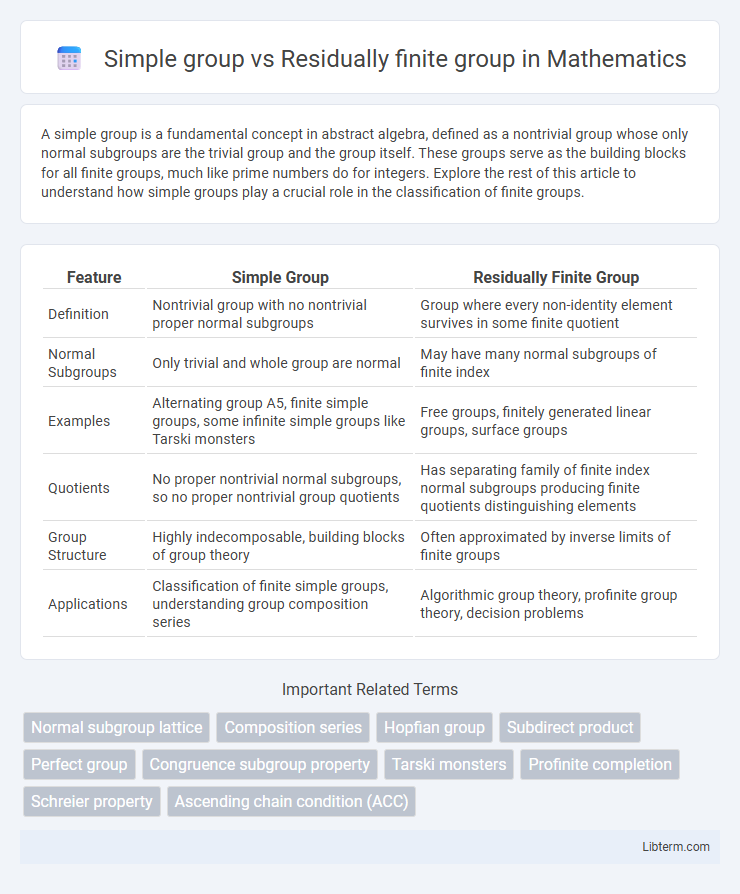
| Feature | Simple Group | Residually Finite Group |
|---|---|---|
| Definition | Nontrivial group with no nontrivial proper normal subgroups | Group where every non-identity element survives in some finite quotient |
| Normal Subgroups | Only trivial and whole group are normal | May have many normal subgroups of finite index |
| Examples | Alternating group A5, finite simple groups, some infinite simple groups like Tarski monsters | Free groups, finitely generated linear groups, surface groups |
| Quotients | No proper nontrivial normal subgroups, so no proper nontrivial group quotients | Has separating family of finite index normal subgroups producing finite quotients distinguishing elements |
| Group Structure | Highly indecomposable, building blocks of group theory | Often approximated by inverse limits of finite groups |
| Applications | Classification of finite simple groups, understanding group composition series | Algorithmic group theory, profinite group theory, decision problems |
Introduction to Simple and Residually Finite Groups
Simple groups are algebraic structures characterized by having no nontrivial normal subgroups, making them fundamental building blocks in group theory. Residually finite groups are defined by their ability to distinguish elements through homomorphisms onto finite groups, ensuring the intersection of all finite index normal subgroups is trivial. The contrast between simple and residually finite groups lies in simplicity's focus on subgroup structure, while residual finiteness emphasizes approximations by finite groups.
Fundamental Definitions and Concepts
A simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself, highlighting its indivisible structure in group theory. A residually finite group is defined by the property that for every non-identity element, there exists a finite index normal subgroup not containing that element, ensuring approximability by finite groups. These fundamental definitions distinguish simplicity by internal subgroup structure and residual finiteness by external finite approximations.
Properties of Simple Groups
Simple groups possess no nontrivial normal subgroups, making them building blocks for group classification and crucial in the classification of finite simple groups, which are well-understood through the classification theorem. Residually finite groups, by contrast, have the property that every non-identity element remains nontrivial in some finite quotient, allowing for approximations by finite groups, but they may not be simple since they often contain proper normal subgroups. The key property of simple groups, especially finite simple groups, is their indivisibility via normal subgroups, which contrasts with the separability and approximation features inherent in residually finite groups.
Properties of Residually Finite Groups
Residually finite groups are characterized by the property that every nontrivial element can be distinguished from the identity in some finite quotient, ensuring a strong connection between the group and its finite images. Unlike simple groups, which have no nontrivial normal subgroups, residually finite groups possess abundant finite index normal subgroups, making them approximable by finite groups. This property enables applications in topology and algebra, such as embedding into profinite groups and solving the word problem effectively.
Key Differences Between Simple Groups and Residually Finite Groups
Simple groups are characterized by having no nontrivial normal subgroups, making them building blocks in group theory, while residually finite groups are defined by their ability to approximate elements via finite quotient groups. A simple group's structure is indivisible without trivial factors, whereas residually finite groups can be distinguished element-wise by homomorphisms onto finite groups. The key difference lies in simplicity denoting an elemental algebraic structure, contrasting with residual finiteness emphasizing separability and approximation by finite images.
Examples of Simple Groups
Finite simple groups include the alternating groups \( A_n \) for \( n \geq 5 \) and the groups of Lie type such as \( \mathrm{PSL}_2(q) \). Infinite simple groups are more rare, with examples like the infinite alternating group and Thompson groups \( T \) and \( V \) known for their unique algebraic properties. Residually finite groups, by contrast, have all nontrivial elements distinguishable in finite quotients, a property not shared by all simple groups.
Examples of Residually Finite Groups
Residually finite groups include free groups, which have the property that every nontrivial element can be distinguished by a homomorphism onto a finite group, and finitely generated abelian groups such as \(\mathbb{Z}^n\). Fundamental groups of compact surfaces and linear groups over fields of characteristic zero also provide classical examples of residually finite groups. Simple groups, in contrast, are often not residually finite since they lack proper nontrivial normal subgroups, but finite simple groups trivially satisfy residual finiteness by definition.
Interactions and Overlaps Between the Two Group Types
Simple groups, characterized by having no nontrivial normal subgroups, rarely intersect with residually finite groups, which are defined by the property that every nontrivial element survives in some finite quotient. However, many finite simple groups are residually finite due to their embeddings in finite structures, linking these concepts through finite group theory. The study of infinite simple groups often reveals deviations from residual finiteness, highlighting the nuanced interplay between simplicity and the residual finiteness condition.
Significance in Group Theory and Applications
Simple groups serve as the fundamental building blocks in group theory, enabling classification of finite groups via the Jordan-Holder theorem, which is critical for understanding group structure at the most basic level. Residually finite groups, characterized by their ability to be approximated by finite groups through finite index normal subgroups, play a crucial role in geometric group theory and topology, especially in the study of 3-manifolds and decision problems. The distinction between these two classes reflects their applications: simple groups are central in pure algebraic classification, while residually finite groups enable effective approximations and computational approaches in infinite group contexts.
Summary and Further Reading
A simple group is a nontrivial group whose only normal subgroups are the trivial group and itself, essential in the classification of finite groups. In contrast, a residually finite group has the property that every nontrivial element survives in some finite quotient, making these groups pivotal in geometric group theory and topology. For further reading, consult "Finite Group Theory" by Michael Aschbacher and "Geometric Group Theory" by Cornelia Drutu and Michael Kapovich for in-depth exploration of these concepts.
Simple group Infographic
 libterm.com
libterm.com