Etale topology provides a framework to study algebraic varieties through covering spaces that mimic local isomorphisms in the complex analytic setting. This approach refines the Zariski topology by incorporating morphisms that are flat and unramified, enabling more delicate geometric and cohomological analysis. Explore the rest of the article to understand how etale topology enhances your insight into modern algebraic geometry.
Table of Comparison
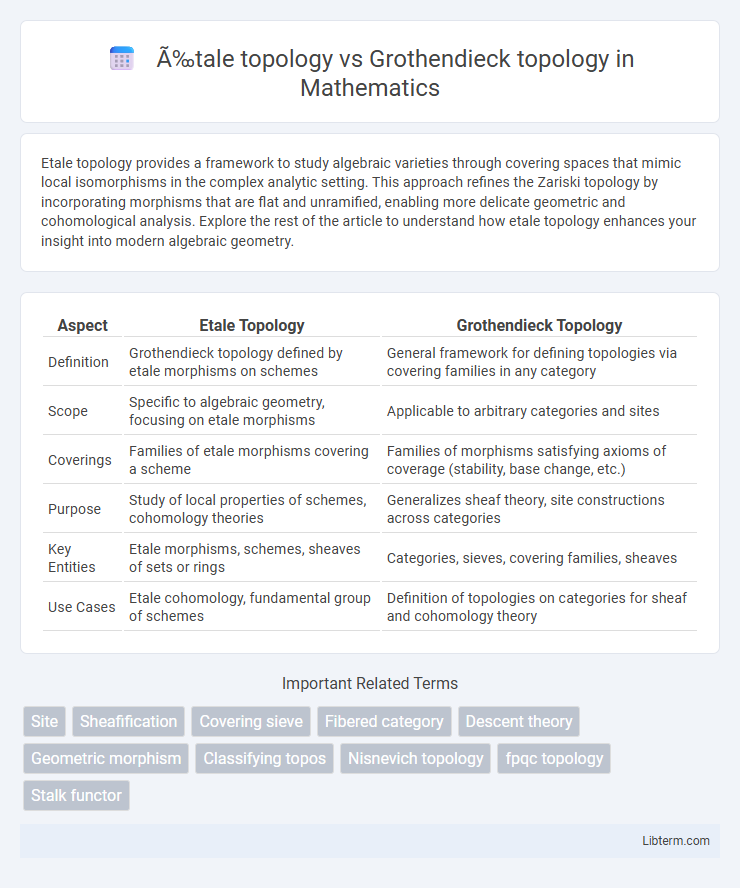
| Aspect | Etale Topology | Grothendieck Topology |
|---|---|---|
| Definition | Grothendieck topology defined by etale morphisms on schemes | General framework for defining topologies via covering families in any category |
| Scope | Specific to algebraic geometry, focusing on etale morphisms | Applicable to arbitrary categories and sites |
| Coverings | Families of etale morphisms covering a scheme | Families of morphisms satisfying axioms of coverage (stability, base change, etc.) |
| Purpose | Study of local properties of schemes, cohomology theories | Generalizes sheaf theory, site constructions across categories |
| Key Entities | Etale morphisms, schemes, sheaves of sets or rings | Categories, sieves, covering families, sheaves |
| Use Cases | Etale cohomology, fundamental group of schemes | Definition of topologies on categories for sheaf and cohomology theory |
Introduction to Topologies in Algebraic Geometry
Etale topology refines the Zariski topology by allowing etale morphisms as covers, enabling finer distinctions in algebraic geometry and facilitating the study of sheaves and cohomology on schemes. Grothendieck topologies generalize classical topologies by defining coverings abstractly through families of morphisms satisfying specific axioms, providing a flexible framework to handle various geometric contexts beyond open sets. The etale topology is a specific instance of a Grothendieck topology that captures local isomorphisms in the etale site, crucial for the development of etale cohomology and its applications in number theory and algebraic geometry.
Overview of Grothendieck Topology
Grothendieck topology generalizes classical topological notions by defining coverings abstractly through sieves on categories, making it a foundational concept in category theory and algebraic geometry. Unlike the etale topology, which is a specific Grothendieck topology using etale morphisms for covering families, Grothendieck topology itself encompasses diverse types of coverings beyond just morphisms of schemes. This abstraction enables the formulation of sheaves and cohomology theories on sites, expanding the scope of geometric and algebraic structures in modern mathematics.
The Fundamentals of Étale Topology
Etale topology is a specialized Grothendieck topology designed to capture local properties of schemes through etale morphisms, which are flat and unramified maps that generalize open immersions. The fundamentals of etale topology revolve around defining a site on a scheme where the covering families consist of etale morphisms, enabling the study of sheaves that reflect finer geometric and arithmetic properties than the Zariski topology. Grothendieck topology provides the abstract framework for this by specifying the criteria for coverings and sheaf conditions, while etale topology applies these concepts to scheme theory with a focus on smooth local behavior and descent theory.
Key Differences Between Étale and Grothendieck Topologies
Etale topology is a specific example of a Grothendieck topology designed for schemes, where covering families consist of etale morphisms, enabling finer local geometric information compared to usual Zariski topology. Grothendieck topology generalizes classical topological notions to categorical settings, allowing the definition of sheaves on abstract sites beyond topological spaces, with coverings defined by sieves satisfying specified axioms. The key difference lies in the scope: etale topology applies to algebraic geometry with explicit etale coverings, while Grothendieck topology provides a unifying framework for defining sheaves and cohomology in vastly diverse mathematical contexts.
The Role of Coverings in Each Topology
Etale topology utilizes etale morphisms as coverings, which are flat, unramified, and locally of finite presentation maps, enabling refined control over local geometric properties. In contrast, Grothendieck topology generalizes the notion of coverings to sieves, allowing any collection of morphisms satisfying axioms like stability under base change and transitivity. The role of coverings in etale topology is to capture the local algebraic structure of schemes with particular smoothness constraints, while Grothendieck topology provides a flexible framework to define sheaves and cohomology on more abstract categories beyond classical topological spaces.
Sheaf Theory in Grothendieck and Étale Contexts
Etale topology is a specific example of a Grothendieck topology designed for algebraic geometry, where coverings consist of etale morphisms reflecting local isomorphisms. Sheaf theory in the Grothendieck context generalizes the notion of sheaves beyond topological spaces to sites, allowing for more flexible and abstract definitions of sheaves and cohomology. In the etale setting, sheaves encode arithmetic and geometric information on schemes via etale morphisms, facilitating etale cohomology theories critical for modern algebraic geometry.
Applications of Étale Topology in Modern Mathematics
Etale topology, a refinement of the Grothendieck topology, plays a crucial role in algebraic geometry by enabling the definition of etale cohomology, which is essential for solving deep problems like the Weil conjectures. It facilitates the study of schemes and their morphisms by allowing locally trivial coverings with respect to etale maps, offering tools that classical topologies cannot provide. Modern applications include number theory, particularly in the development of arithmetic geometry, and in the proof of the Mordell-Weil theorem and parts of the Langlands program.
Comparing Site Structures and Morphisms
Etale topology is a specific type of Grothendieck topology defined on the category of schemes, where coverings are given by etale morphisms that are flat and unramified, ensuring local isomorphisms in the etale sense. Grothendieck topology generalizes site structures by specifying coverings abstractly as families of morphisms satisfying axioms, allowing various types such as Zariski, etale, and fppf topologies, each refining the notion of localization and descent. Comparing site structures involves analyzing how morphisms behave under these coverings, where etale topology's emphasis on unramified and smooth morphisms provides finer local data compared to more general Grothendieck topologies, impacting sheaf behavior and cohomological properties.
Pros and Cons: Étale Topology vs. Grothendieck Topology
Etale topology specializes in algebraic geometry by enabling powerful cohomological tools like etale cohomology, which are key for studying schemes over non-algebraically closed fields, but it is limited to morphisms that are etale, restricting its generality. Grothendieck topology, as a broader framework, accommodates various coverings beyond open sets, offering flexibility for defining sheaves in different contexts but often at the cost of increased abstraction and complexity. While etale topology provides concrete geometric intuition and effective tools for number-theoretic problems, Grothendieck topologies facilitate extensive generalizations in category theory and topology, making each suitable for distinct mathematical goals.
Conclusion: Choosing the Right Topological Framework
Etale topology provides a finer structure useful for studying algebraic varieties through local isomorphisms and has strong connections with Galois theory and algebraic geometry. Grothendieck topology generalizes classical topologies by defining coverings abstractly, allowing for versatile applications in sheaf theory and topos theory beyond algebraic geometry. Selecting the appropriate framework depends on the desired balance between geometric intuition and categorical generality, where etale topology suits schemes and arithmetic problems, while Grothendieck topology offers broader categorical flexibility.
Étale topology Infographic
 libterm.com
libterm.com