Symmetry groups describe the set of all transformations, such as rotations and reflections, that leave an object unchanged, playing a crucial role in geometry and physics. Understanding these groups helps reveal the inherent balance and structure within natural and mathematical forms. Explore the rest of the article to deepen your grasp on how symmetry groups illuminate patterns in your everyday world.
Table of Comparison
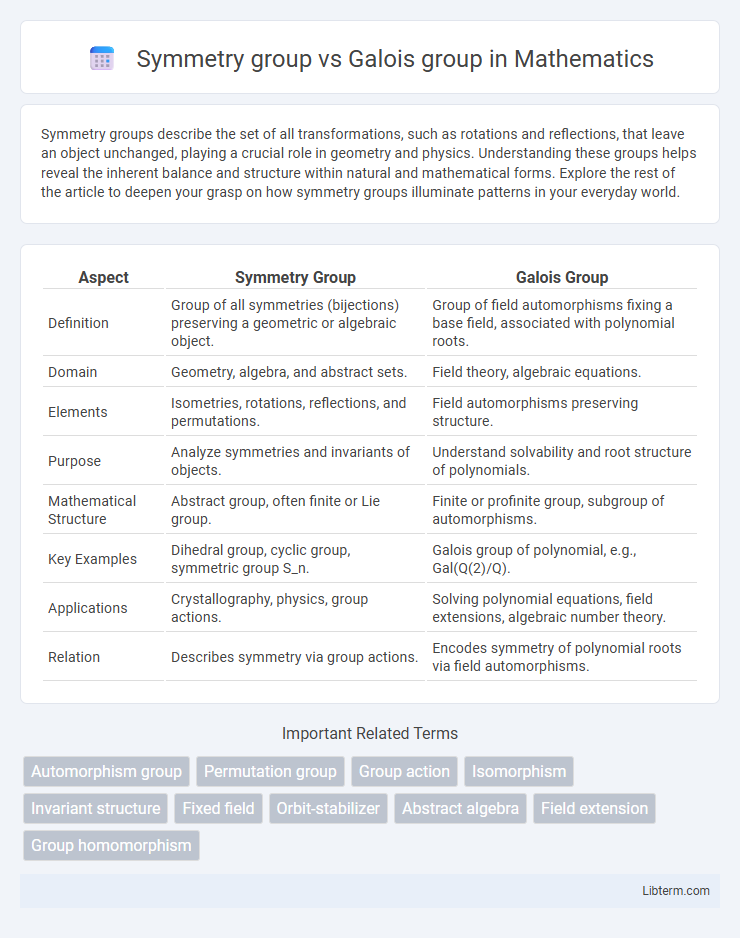
| Aspect | Symmetry Group | Galois Group |
|---|---|---|
| Definition | Group of all symmetries (bijections) preserving a geometric or algebraic object. | Group of field automorphisms fixing a base field, associated with polynomial roots. |
| Domain | Geometry, algebra, and abstract sets. | Field theory, algebraic equations. |
| Elements | Isometries, rotations, reflections, and permutations. | Field automorphisms preserving structure. |
| Purpose | Analyze symmetries and invariants of objects. | Understand solvability and root structure of polynomials. |
| Mathematical Structure | Abstract group, often finite or Lie group. | Finite or profinite group, subgroup of automorphisms. |
| Key Examples | Dihedral group, cyclic group, symmetric group S_n. | Galois group of polynomial, e.g., Gal(Q(2)/Q). |
| Applications | Crystallography, physics, group actions. | Solving polynomial equations, field extensions, algebraic number theory. |
| Relation | Describes symmetry via group actions. | Encodes symmetry of polynomial roots via field automorphisms. |
Introduction to Symmetry Groups and Galois Groups
Symmetry groups describe the set of all transformations preserving the structure of mathematical objects, such as geometric figures or algebraic structures, encoding spatial symmetries through group theory. Galois groups arise in field theory and abstract algebra, characterizing the symmetries of the roots of polynomial equations and revealing deep connections between field extensions and group theory. Both concepts leverage group actions to analyze symmetries but differ in focus: symmetry groups apply broadly to geometric contexts, while Galois groups connect field automorphisms with solvability of polynomials.
Historical Origins and Development
The study of symmetry groups originated in the 19th century with Evariste Galois, who introduced group theory to understand polynomial equation solvability through permutations of roots, marking the foundation of Galois groups. Symmetry groups, formalized by Augustin-Louis Cauchy and Camille Jordan, evolved as abstract structures capturing geometric and algebraic symmetries beyond polynomial contexts. This historical development positioned Galois groups as a specialized application of symmetry groups, emphasizing algebraic field extensions and their automorphisms.
Core Definitions: Symmetry Group Explained
A symmetry group consists of all transformations preserving the structure of a mathematical object, such as rotations and reflections maintaining geometric shape. The Galois group, a specific type of symmetry group, describes permutations of roots of a polynomial that leave algebraic relations invariant. Understanding the symmetry group provides a foundational framework to analyze Galois groups, linking abstract algebraic structures to geometric and polynomial behaviors.
Core Definitions: Galois Group Demystified
The Galois group is a fundamental concept in abstract algebra that describes the group of field automorphisms of a field extension, capturing the symmetries of roots of a polynomial equation. Unlike a general symmetry group that can represent geometric or combinatorial symmetries, the Galois group specifically encodes how field elements permute while preserving field operations. This core idea connects polynomial roots to group theory, enabling profound results such as solvability by radicals and the classification of algebraic equations.
Structural Differences: Symmetry vs. Galois Groups
Symmetry groups describe geometric transformations preserving the structure of objects, emphasizing spatial invariance and group actions on physical shapes. Galois groups focus on field automorphisms capturing algebraic symmetries of polynomial roots, reflecting deeper algebraic field extensions and solving equations. The fundamental distinction lies in symmetry groups' geometric interpretations versus Galois groups' role in understanding algebraic solvability and field theory.
Applications in Mathematics and Science
Symmetry groups classify geometric and algebraic structures by describing their invariances under transformations, crucial in crystallography, physics, and chemistry for analyzing molecular symmetries and particle interactions. Galois groups, arising from field extensions in algebra, provide tools to solve polynomial equations by linking group theory to field theory, playing a key role in number theory and algebraic geometry. Both groups underpin modern mathematics, with symmetry groups informing spatial and physical intuitions, while Galois groups enable deep insights into solvability and structural properties of algebraic equations.
Group Actions in Geometry and Algebra
Symmetry groups characterize geometric objects by describing transformations that preserve structure, acting on shapes to capture rotational, reflective, and translational symmetries. Galois groups arise in algebra by encoding automorphisms of field extensions, linking polynomial roots through group actions that reveal solvability and field structure. Both symmetry groups and Galois groups utilize group actions to connect algebraic properties with geometric or field-theoretic invariants, highlighting deep interplay between geometry and algebra in modern mathematics.
Notable Examples: Polygons & Polynomial Equations
The symmetry group of a polygon, such as the dihedral group \(D_n\), captures geometric transformations like rotations and reflections preserving its shape. The Galois group of a polynomial equation encodes algebraic symmetries among its roots, with classic examples including the symmetric group \(S_n\) governing general polynomial equations of degree \(n\). Notably, the interplay between dihedral groups and Galois groups arises in solving polynomial equations linked to regular polygons, illuminating connections between geometry and field theory.
Connections and Overlaps Between Symmetry and Galois Groups
Symmetry groups and Galois groups both capture structural invariances in mathematical objects, with symmetry groups describing geometric or combinatorial symmetries while Galois groups encode field extensions' automorphisms. The connection between these groups is exemplified in the study of polynomial roots, where the Galois group acts by permuting roots, mirroring the symmetric group actions on sets. Overlaps arise in algebraic geometry and number theory, where the symmetry group of a geometric object influences the Galois group of associated field extensions, linking group actions to arithmetic properties.
Conclusion: Significance in Modern Mathematics
The symmetry group captures the geometric or combinatorial symmetries of an object, while the Galois group encodes the algebraic symmetries of field extensions and polynomial roots. Both groups serve as fundamental tools in modern mathematics, linking abstract algebra, number theory, and geometry through their symmetry-based frameworks. Their interplay underpins major advances such as the resolution of polynomial solvability, classification of fields, and the development of modern algebraic geometry.
Symmetry group Infographic
 libterm.com
libterm.com