Commutative properties in mathematics refer to operations where changing the order of the numbers does not affect the result, such as addition and multiplication. This fundamental concept simplifies calculations and enhances problem-solving efficiency. Explore the rest of the article to deepen your understanding of commutative operations and their applications.
Table of Comparison
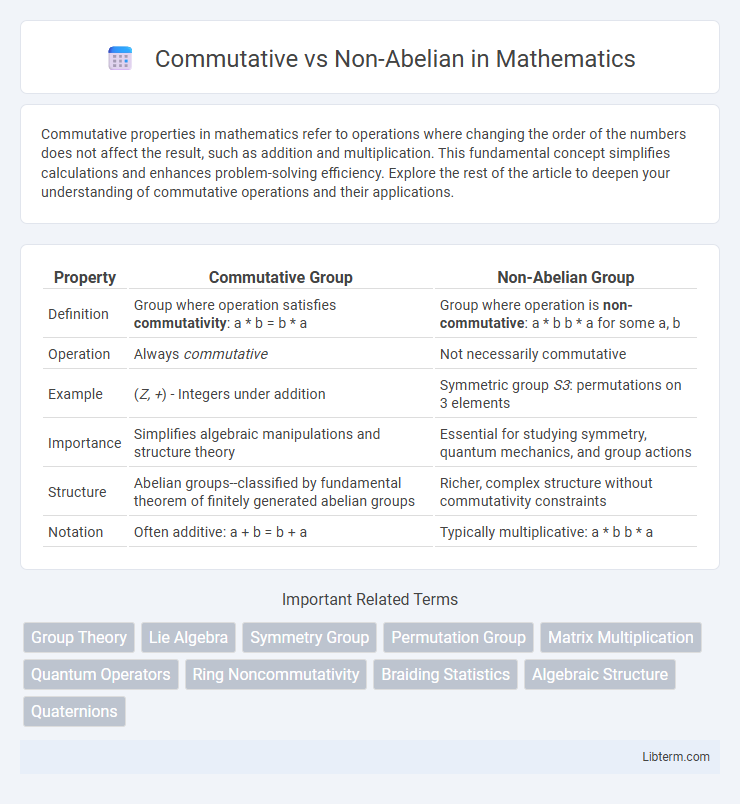
| Property | Commutative Group | Non-Abelian Group |
|---|---|---|
| Definition | Group where operation satisfies commutativity: a * b = b * a | Group where operation is non-commutative: a * b b * a for some a, b |
| Operation | Always commutative | Not necessarily commutative |
| Example | (Z, +) - Integers under addition | Symmetric group S3: permutations on 3 elements |
| Importance | Simplifies algebraic manipulations and structure theory | Essential for studying symmetry, quantum mechanics, and group actions |
| Structure | Abelian groups--classified by fundamental theorem of finitely generated abelian groups | Richer, complex structure without commutativity constraints |
| Notation | Often additive: a + b = b + a | Typically multiplicative: a * b b * a |
Introduction to Commutative and Non-Abelian Structures
Commutative structures, often seen in algebraic systems like Abelian groups, satisfy the property that the order of operation does not affect the outcome (a * b = b * a). Non-Abelian structures, in contrast, exhibit non-commutative behavior where the sequence of operations changes the result, fundamental in areas such as group theory and quantum mechanics. Understanding these distinctions is crucial for exploring symmetry, algebraic topology, and particle interactions within mathematics and physics.
Defining Commutative (Abelian) Operations
Commutative (Abelian) operations are defined by the property that changing the order of the operands does not affect the result, commonly expressed as a * b = b * a for all elements a and b in a set. These operations are fundamental in algebraic structures known as Abelian groups, where both commutativity and associativity hold true. Understanding commutative operations is crucial for fields such as number theory, linear algebra, and many branches of abstract algebra.
Understanding Non-Abelian (Non-Commutative) Operations
Non-Abelian operations are characterized by the property that the order of application affects the outcome, meaning ab ba in general, which contrasts with commutative operations where ab = ba. In mathematical structures such as groups, non-Abelian groups have elements whose multiplication does not commute, playing a critical role in advanced fields like quantum mechanics and particle physics. Understanding non-Abelian operations involves analyzing the structure's non-commutative nature, which significantly influences symmetry properties and transformations in complex systems.
Mathematical Foundations and Examples
Commutative operations, fundamental in algebraic structures like abelian groups and fields, satisfy the property a x b = b x a, ensuring interchangeable operands yield the same result. Non-Abelian, or non-commutative, structures such as matrix multiplication or the symmetry group of a triangle, do not adhere to this property, exemplifying complexity in group theory and quantum mechanics. These distinctions underpin key mathematical concepts in abstract algebra, influencing areas from topology to particle physics.
Key Differences: Commutative vs Non-Abelian
Commutative (Abelian) groups feature operations where the order of elements does not affect the result, expressed as \(a \cdot b = b \cdot a\) for all elements \(a\) and \(b\). Non-Abelian groups exhibit non-commutative behavior, meaning that the operation \(a \cdot b\) may not equal \(b \cdot a\), reflecting more complex structural properties. This fundamental difference influences group theory applications in physics, cryptography, and symmetry analysis.
Importance in Algebra and Group Theory
Commutative, or Abelian, groups simplify algebraic structures by ensuring the order of operation does not affect the outcome, facilitating easier problem-solving and proofs. Non-Abelian groups, where the order matters, play a crucial role in advanced algebra and theoretical physics, particularly in the study of symmetries and group actions. Understanding the distinction between commutative and non-Abelian groups is fundamental in group theory as it impacts the classification and application of groups in various mathematical and scientific contexts.
Real-World Applications of Commutative Structures
Commutative structures, such as Abelian groups and commutative rings, play a crucial role in cryptography, error-correcting codes, and signal processing due to their predictable and symmetric operations. Real-world applications include RSA encryption, which relies on the commutative properties of modular arithmetic for secure data transmission. In contrast, non-Abelian groups are essential in particle physics and quantum mechanics, where non-commutative operations model complex symmetries and interactions.
Real-World Applications of Non-Abelian Structures
Non-Abelian groups play a crucial role in quantum physics, particularly in the study of particle interactions governed by gauge theories like the Standard Model, where symmetry operations do not commute. These structures are essential in cryptography for designing secure protocols based on non-commutative algebraic frameworks, enhancing resistance to certain types of cyber-attacks. Robotics and 3D computer graphics also rely on non-Abelian mathematics to handle rotations and transformations in spatial modeling, enabling precise control and realistic rendering.
Challenges in Working with Non-Abelian Systems
Non-Abelian systems, characterized by operations where order affects the outcome, present significant challenges in mathematical modeling and quantum physics due to their intrinsic non-commutativity. The complexity of calculations increases as these systems often involve higher-dimensional representations and more intricate algebraic structures, complicating both theoretical analysis and computational algorithms. Understanding and manipulating non-Abelian groups require advanced techniques in abstract algebra and group theory, which are essential for applications in particle physics, cryptography, and topological quantum computing.
Summary and Implications for Further Study
Commutative (Abelian) groups exhibit the property that the group operation is independent of the order of elements, simplifying analysis and applications in fields like number theory and coding. Non-Abelian groups, where the order affects the outcome, introduce greater complexity but allow for richer structures essential in advanced physics, cryptography, and topology. Understanding the distinction between these group types is crucial for further study in mathematics and theoretical physics, impacting the development of symmetry theories and quantum mechanics.
Commutative Infographic
 libterm.com
libterm.com