Homeomorphism is a fundamental concept in topology that describes a continuous, bijective mapping between two spaces with a continuous inverse, preserving their topological properties. Understanding homeomorphisms allows you to classify spaces based on their intrinsic shape rather than rigid geometric measures. Explore the rest of the article to see how homeomorphisms distinguish between surfaces and influence modern mathematics.
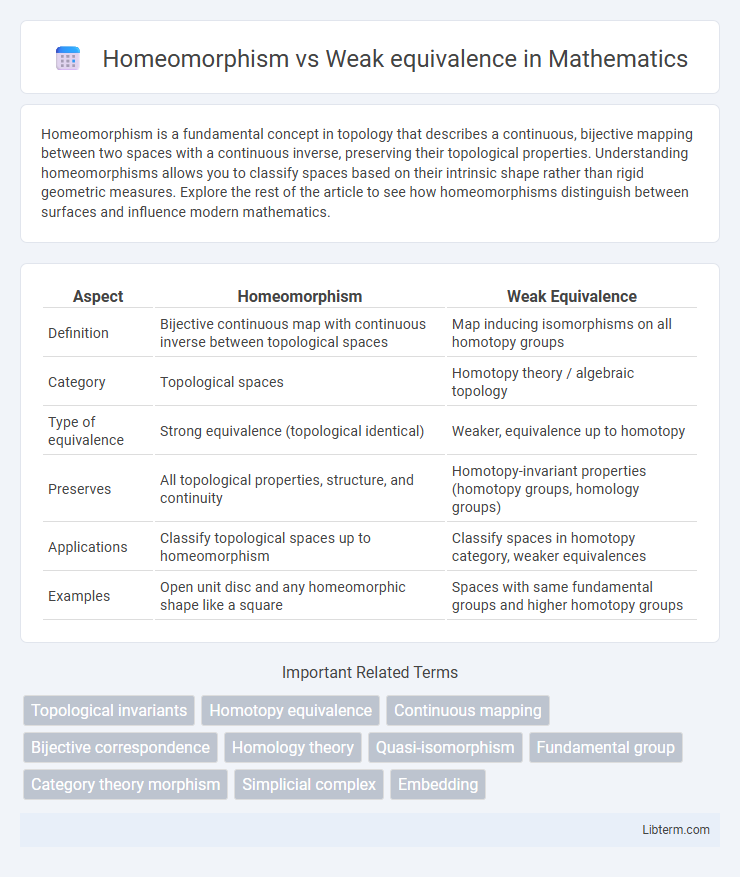
Table of Comparison
| Aspect | Homeomorphism | Weak Equivalence |
|---|---|---|
| Definition | Bijective continuous map with continuous inverse between topological spaces | Map inducing isomorphisms on all homotopy groups |
| Category | Topological spaces | Homotopy theory / algebraic topology |
| Type of equivalence | Strong equivalence (topological identical) | Weaker, equivalence up to homotopy |
| Preserves | All topological properties, structure, and continuity | Homotopy-invariant properties (homotopy groups, homology groups) |
| Applications | Classify topological spaces up to homeomorphism | Classify spaces in homotopy category, weaker equivalences |
| Examples | Open unit disc and any homeomorphic shape like a square | Spaces with same fundamental groups and higher homotopy groups |
Understanding Homeomorphism: Definition and Core Concepts
Homeomorphism is a bijective continuous function between topological spaces with a continuous inverse, preserving topological properties such as connectedness and compactness. It serves as a fundamental concept in topology to identify spaces that are essentially the same in shape, allowing deformation without tearing or gluing. Understanding homeomorphisms involves recognizing that they establish an equivalence relation, classifying spaces based on their intrinsic geometric structure rather than metric details.
Exploring Weak Equivalence in Topology
Weak equivalence in topology refers to a continuous map between topological spaces inducing isomorphisms on all homotopy groups, making it weaker than homeomorphism, which requires a bijective continuous map with continuous inverse. While a homeomorphism preserves all topological properties exactly, a weak equivalence only preserves homotopy type, allowing spaces to differ in finer structures. This concept plays a crucial role in homotopy theory and model categories, where weak equivalences facilitate classification up to homotopy rather than strict equivalence.
Key Differences Between Homeomorphism and Weak Equivalence
Homeomorphism is a bijective continuous map between topological spaces with a continuous inverse, ensuring a perfect topological equivalence that preserves all open sets and structures. Weak equivalence, in homotopy theory, refers to a map inducing isomorphisms on all homotopy groups, capturing similarity up to homotopy rather than strict topological identity. The key difference lies in homeomorphism preserving exact topology, while weak equivalence preserves homotopy type, allowing deformation but not necessarily exact structural matching.
Topological Spaces: Homeomorphism vs Weak Equivalence
Homeomorphisms are bijective continuous functions with continuous inverses between topological spaces, preserving their exact topological structure and ensuring the spaces are topologically identical. Weak equivalences, defined in homotopy theory, induce isomorphisms on all homotopy groups and preserve the homotopy type, allowing spaces to be considered equivalent up to "deformations" rather than strict homeomorphism. While homeomorphisms require precise point-to-point correspondence, weak equivalences focus on the preservation of fundamental categorical properties, making them critical in algebraic topology and model category theory.
Criteria for Homeomorphism: When Are Spaces Truly ‘The Same’?
Homeomorphism between topological spaces requires a continuous bijection with a continuous inverse, ensuring spaces are topologically identical with preserved open set structures. This criterion guarantees that properties like connectedness, compactness, and continuity of functions remain invariant, distinguishing true equivalence from weaker notions. In contrast, weak equivalence, commonly used in homotopy theory, stresses homotopy group isomorphisms rather than exact topological matching, highlighting a more flexible similarity concept.
Weak Equivalence: Fundamental Group and Homotopy Insights
Weak equivalence in topology refers to maps that induce isomorphisms on all homotopy groups, particularly the fundamental group, capturing essential homotopy-type information without requiring a homeomorphism. Unlike homeomorphisms, which are bijective continuous maps with continuous inverses preserving exact topological structure, weak equivalences preserve homotopy equivalence classes and fundamental group structures up to isomorphism. These insights are crucial in algebraic topology, where weak equivalences classify spaces based on their homotopy features rather than strict geometric identity.
Examples Illustrating Homeomorphism and Weak Equivalence
Homeomorphism describes a continuous, bijective map with a continuous inverse between topological spaces, such as the equivalence between a coffee cup and a doughnut, illustrating their shared topological structure. Weak equivalence in homotopy theory refers to maps inducing isomorphisms on all homotopy groups, exemplified by the inclusion of a deformation retract, like a circle embedded in a filled disk. Both concepts capture intrinsic similarities between spaces, but homeomorphism is a stronger condition preserving exact topological properties, whereas weak equivalence focuses on homotopy-invariant features.
Applications in Algebraic Topology: Why the Distinction Matters
Homeomorphisms provide a bijective, continuous mapping with continuous inverse, preserving topological properties exactly, essential for classification in algebraic topology. Weak equivalences, defined by inducing isomorphisms on all homotopy groups, allow flexibility in homotopy theory, enabling equivalence of spaces up to deformation rather than strict shape preservation. Distinguishing between these concepts is crucial when working with homotopy types, spectral sequences, and model categories, where weak equivalences facilitate computations and theoretical advances beyond rigid homeomorphic classification.
Limitations and Misconceptions: Clearing Up Confusion
Homeomorphisms strictly preserve topological equivalence by establishing a continuous bijection with a continuous inverse, whereas weak equivalences allow for more flexible homotopical equivalences that need not be bijections, leading to common misconceptions about their interchangeability. A key limitation is that weak equivalences can identify spaces with very different geometric or topological structures, which homeomorphisms cannot, causing confusion in their application for classification problems. Clarifying these distinctions requires emphasizing that homeomorphisms guarantee identical topological spaces, while weak equivalences identify spaces up to homotopy, impacting their use in algebraic topology and homotopy theory.
Summary Table: Homeomorphism vs Weak Equivalence at a Glance
Homeomorphism is a bijective continuous map with a continuous inverse, preserving topological structure exactly, while weak equivalence, often used in homotopy theory, identifies spaces that share the same homotopy type but may differ in finer topological details. The summary table highlights that homeomorphisms imply structural identity, maintaining all topological properties, whereas weak equivalences guarantee equivalence only up to homotopy, focusing on higher-level connectivity and deformation features. Key distinctions include strict invertibility and preservation of open sets in homeomorphisms, contrasted with the more flexible, homotopy-based criteria for weak equivalences.
Homeomorphism Infographic
 libterm.com
libterm.com