Order plays a crucial role in achieving efficiency and clarity in both personal and professional settings. Establishing a structured system reduces chaos, saves time, and enhances productivity, allowing you to focus on what truly matters. Explore the rest of this article to discover practical strategies for creating and maintaining effective order in your life.
Table of Comparison
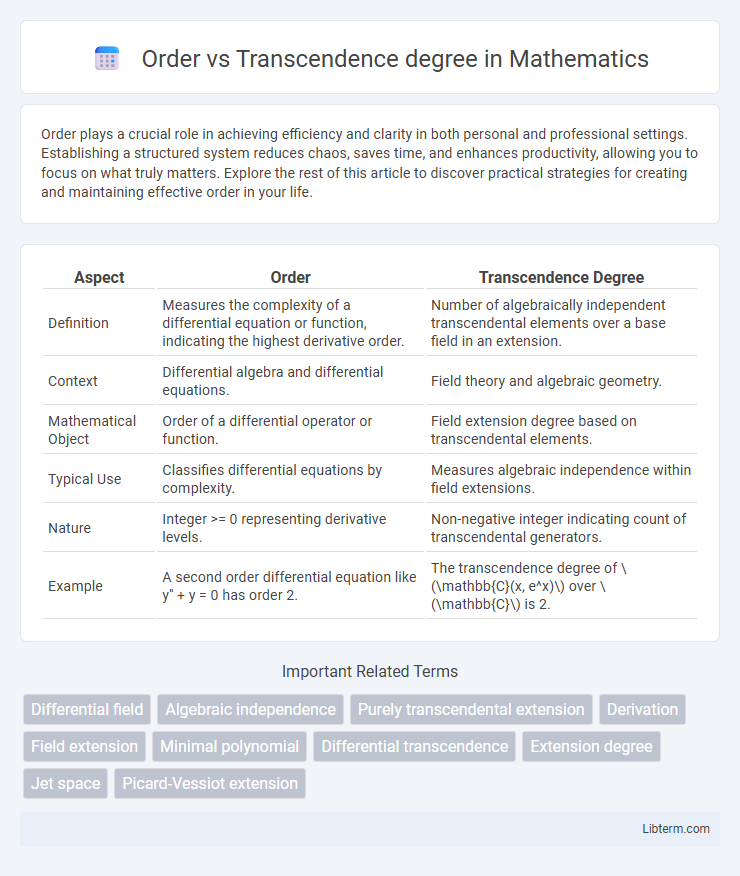
| Aspect | Order | Transcendence Degree |
|---|---|---|
| Definition | Measures the complexity of a differential equation or function, indicating the highest derivative order. | Number of algebraically independent transcendental elements over a base field in an extension. |
| Context | Differential algebra and differential equations. | Field theory and algebraic geometry. |
| Mathematical Object | Order of a differential operator or function. | Field extension degree based on transcendental elements. |
| Typical Use | Classifies differential equations by complexity. | Measures algebraic independence within field extensions. |
| Nature | Integer >= 0 representing derivative levels. | Non-negative integer indicating count of transcendental generators. |
| Example | A second order differential equation like y'' + y = 0 has order 2. | The transcendence degree of \(\mathbb{C}(x, e^x)\) over \(\mathbb{C}\) is 2. |
Introduction to Order and Transcendence Degree
Order measures the growth rate of solutions to differential equations, specifically quantifying the complexity of their behavior using integer or fractional values. Transcendence degree evaluates the algebraic independence of functions or elements over a given field, determining how many of them cannot be expressed as roots of polynomial equations with coefficients from that field. Understanding the order and transcendence degree provides essential insight into the structure and solvability of differential fields and differential algebraic functions.
Defining Algebraic Order and Its Significance
Algebraic order measures the minimum number of algebraic relations needed to define an element over a base field, serving as a critical concept in field theory. This order quantifies the complexity of algebraic dependencies and directly impacts the transcendence degree, which counts the maximal number of algebraically independent elements. Understanding algebraic order is essential for classifying field extensions and analyzing algebraic structures within mathematical frameworks.
Understanding Transcendence Degree
The transcendence degree measures the maximum number of algebraically independent elements over a base field within a field extension, serving as a crucial invariant in field theory. Unlike order, which typically quantifies size or hierarchy in algebraic structures, transcendence degree captures the complexity and dimensionality of extensions that contain transcendental elements. Understanding transcendence degree facilitates the classification of field extensions, aids in the study of transcendental numbers, and underpins applications in algebraic geometry and number theory.
Differences Between Order and Transcendence Degree
Order measures the maximum number of derivatives needed to express a differential field extension element, reflecting algebraic complexity, while transcendence degree counts the number of algebraically independent elements over the base field, indicating the extension's "size." The order is tied to differential equations and their solutions' behavior, whereas transcendence degree relates to purely algebraic independence without differentiation. These concepts differ fundamentally: order captures the depth of differential relations, and transcendence degree quantifies algebraic freedom in the extension.
The Role of Order in Field Extensions
Order in field extensions determines the structural complexity and hierarchy of algebraic elements within the extension, affecting how transcendence degree measures the number of algebraically independent transcendental elements over the base field. The concept of order influences the arrangement and generation of subextensions, guiding the classification of extensions as algebraic or transcendental. Understanding order facilitates clearer distinctions between finite and infinite extensions, directly impacting the evaluation of transcendence degree in function fields and algebraic geometry contexts.
How Transcendence Degree Measures Algebraic Independence
Transcendence degree quantifies the size of the largest algebraically independent subset within a field extension, distinguishing transcendental elements from algebraic ones. While order relates to the structure or complexity of algebraic objects, transcendence degree specifically measures the degree of algebraic independence by counting elements that satisfy no polynomial relations over the base field. This metric provides a precise way to analyze extensions in terms of freedom from algebraic constraints, making it fundamental in field theory and algebraic geometry.
Examples Illustrating Order and Transcendence Degree
In field theory, the order of an element over a base field refers to the minimal polynomial's degree, while the transcendence degree measures the size of the largest algebraically independent subset over that field. For example, in the extension \(\mathbb{Q}(\sqrt{2})/\mathbb{Q}\), the element \(\sqrt{2}\) has order 2, corresponding to its minimal polynomial \(x^2 - 2\), and the transcendence degree is 0 since \(\sqrt{2}\) is algebraic. Conversely, for the extension \(\mathbb{Q}(x)/\mathbb{Q}\) where \(x\) is transcendental, the element \(x\) has infinite order, and the transcendence degree is 1, as \(x\) forms a transcendence basis of the extension.
Applications in Algebraic Geometry and Field Theory
Order and transcendence degree serve as crucial invariants in algebraic geometry and field theory, where the order of a differential equation reflects the complexity of algebraic varieties' local behavior. Transcendence degree quantifies the size of a field extension by counting algebraically independent elements, essential in classifying function fields of algebraic varieties. Applications include characterizing dimensions of varieties, understanding algebraic dependence relations, and studying differential algebraic structures within field extensions.
Challenges in Calculating Order and Transcendence Degree
Calculating the order of a differential equation involves determining the highest derivative present, which becomes complicated when dealing with nonlinear or partial differential equations due to their implicit and multi-variable nature. Transcendence degree calculation requires assessing the algebraic independence of a field extension, often hindered by intricate dependencies and the complexity of the underlying algebraic structures. Both challenges demand sophisticated algebraic and differential tools, such as differential algebra and algebraic geometry, to effectively analyze and compute these invariants in advanced mathematical contexts.
Conclusion: Interplay Between Order and Transcendence Degree
The interplay between order and transcendence degree reveals that the complexity of algebraic structures is deeply influenced by both parameters. Higher transcendence degree often correlates with increased algebraic independence, impacting the order by extending the dimensional hierarchy within the structure. Understanding this relationship facilitates advancements in differential algebra and model theory by characterizing the foundational growth patterns of differential fields.
Order Infographic
 libterm.com
libterm.com