Harmonic refers to frequencies that are integer multiples of a fundamental tone, playing a crucial role in sound quality and musical timbre. Understanding harmonics can enhance your appreciation of music and improve sound engineering techniques. Discover more about harmonics and their impact in the rest of this article.
Table of Comparison
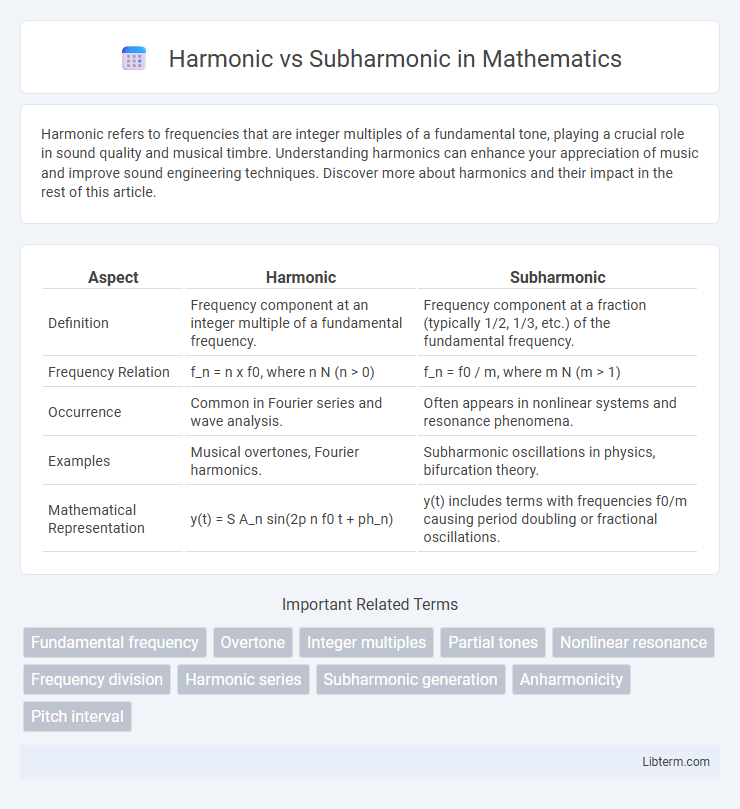
| Aspect | Harmonic | Subharmonic |
|---|---|---|
| Definition | Frequency component at an integer multiple of a fundamental frequency. | Frequency component at a fraction (typically 1/2, 1/3, etc.) of the fundamental frequency. |
| Frequency Relation | f_n = n x f0, where n N (n > 0) | f_n = f0 / m, where m N (m > 1) |
| Occurrence | Common in Fourier series and wave analysis. | Often appears in nonlinear systems and resonance phenomena. |
| Examples | Musical overtones, Fourier harmonics. | Subharmonic oscillations in physics, bifurcation theory. |
| Mathematical Representation | y(t) = S A_n sin(2p n f0 t + ph_n) | y(t) includes terms with frequencies f0/m causing period doubling or fractional oscillations. |
Introduction to Harmonics and Subharmonics
Harmonics are integer multiples of a fundamental frequency, contributing to the richness and complexity of sound waves in acoustics and signal processing. Subharmonics, on the other hand, are frequencies that are fractions of the fundamental frequency, often found in nonlinear systems and musical contexts to create unique tonal effects. Understanding harmonics and subharmonics is essential for analyzing waveforms, designing audio equipment, and studying vibration phenomena.
Understanding Harmonic Frequencies
Harmonic frequencies are integer multiples of a fundamental frequency, creating a series of tones that reinforce the original sound's pitch and timbre. In contrast, subharmonics occur at fractional divisions of the fundamental frequency, producing lower-pitched tones that enrich the overall sound spectrum. Understanding harmonic frequencies is crucial for applications in acoustics, signal processing, and musical instrument design, as they determine sound quality and resonance characteristics.
What are Subharmonics?
Subharmonics are frequency components in a signal that occur at fractional multiples (e.g., half or one-third) of the fundamental frequency, contrasting with harmonics which occur at integer multiples. These frequencies arise from nonlinear system dynamics, such as in mechanical vibrations, acoustics, and electronic circuits, and indicate complex resonance behaviors or instabilities. Identifying subharmonics is crucial for diagnosing system performance, predicting faults, and enhancing signal analysis in engineering and physics applications.
Key Differences Between Harmonics and Subharmonics
Harmonics are integer multiples of a fundamental frequency, while subharmonics occur at fractional multiples below the fundamental frequency. Harmonics typically arise in resonant systems and signal processing, enhancing the frequency spectrum, whereas subharmonics often indicate nonlinear behavior and can cause signal distortion or modulation effects. The key difference lies in their frequency relations: harmonics increase frequency components above the fundamental, whereas subharmonics introduce lower frequency components that influence system stability and response.
Mathematical Representation of Harmonics and Subharmonics
Harmonics are mathematically represented as integer multiples of a fundamental frequency \( f_0 \), expressed as \( f_n = n \cdot f_0 \) where \( n \in \mathbb{Z}^+ \). Subharmonics correspond to fractional multiples of the fundamental frequency, typically denoted as \( f_m = \frac{f_0}{m} \) with \( m \in \mathbb{Z}^+ \), producing frequencies lower than \( f_0 \). This distinction allows harmonics to reinforce the fundamental frequency's waveform while subharmonics introduce oscillations at frequencies below the fundamental.
Real-World Examples of Harmonics
Harmonics occur when signals or waves vibrate at integer multiples of a fundamental frequency, commonly observed in musical instruments like guitars and pianos where string vibrations produce rich tonal overtones. In electrical engineering, power systems generate harmonics due to non-linear loads such as variable frequency drives and fluorescent lighting, impacting power quality and causing equipment inefficiency. Acoustic resonance in architectural spaces, such as organ pipes and concert halls, also relies on harmonic frequencies to enhance sound clarity and depth.
Practical Applications of Subharmonics
Subharmonics find practical applications in vibration analysis for machinery diagnostics, where they help identify faults like misalignment or bearing defects by detecting frequency components at fractional multiples of the fundamental frequency. In acoustics, subharmonics play a crucial role in sound therapy and musical instrument design by generating unique tonal qualities below the fundamental pitch. Their ability to reveal hidden nonlinear behaviors in mechanical and acoustic systems makes subharmonics invaluable for condition monitoring and innovative audio engineering.
Importance in Signal Processing and Audio Engineering
Harmonics refer to integral multiples of a fundamental frequency that enrich sound quality and improve signal clarity in audio engineering. Subharmonics, occurring at fractional frequencies of the fundamental, add depth and bass presence, crucial for enhancing low-frequency signals in music production and sound design. Understanding the balance between harmonics and subharmonics enables precise control over timbre and tonal texture, optimizing audio fidelity and signal processing outcomes.
Challenges in Detecting Harmonics vs Subharmonics
Detecting harmonics poses challenges due to their integer-multiple frequencies that often overlap with fundamental signals, requiring precise spectral analysis to differentiate them accurately. Subharmonics, occurring at fractional frequencies, complicate detection further because they can be masked by noise or nonlinear system responses, demanding advanced signal processing techniques like time-frequency analysis or wavelet transforms. Both harmonics and subharmonics detection face difficulties from signal distortions and varying amplitude levels, necessitating robust algorithms for reliable identification in complex environments.
Future Trends and Research in Harmonic and Subharmonic Analysis
Future trends in harmonic and subharmonic analysis emphasize advances in machine learning algorithms for improved signal decomposition and noise reduction. Research increasingly explores real-time applications in biomedical engineering and telecommunications, aiming to enhance precision in complex wave pattern recognition. Emerging studies focus on integrating quantum computing to accelerate computations and enable higher-dimensional harmonic mapping.
Harmonic Infographic
 libterm.com
libterm.com