Concrete categories are mathematical structures that consist of objects and morphisms, equipped with a faithful functor to the category of sets, allowing each object to be seen as a set with additional structure. These categories provide a framework for studying algebraic structures and their homomorphisms through familiar set-theoretic terms. Explore the rest of the article to deepen your understanding of concrete categories and their applications in mathematics.
Table of Comparison
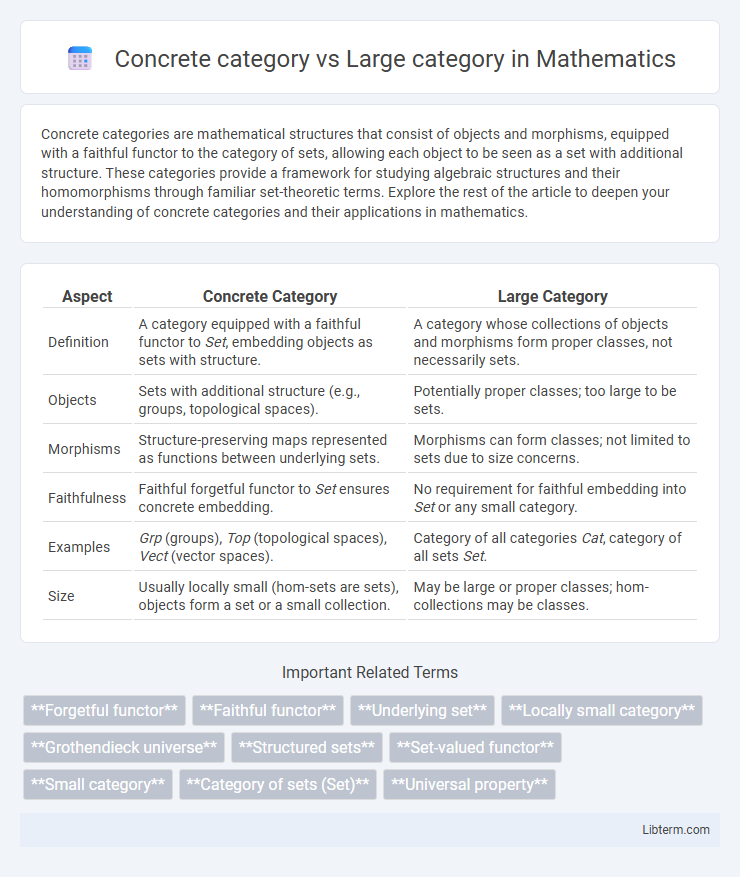
| Aspect | Concrete Category | Large Category |
|---|---|---|
| Definition | A category equipped with a faithful functor to Set, embedding objects as sets with structure. | A category whose collections of objects and morphisms form proper classes, not necessarily sets. |
| Objects | Sets with additional structure (e.g., groups, topological spaces). | Potentially proper classes; too large to be sets. |
| Morphisms | Structure-preserving maps represented as functions between underlying sets. | Morphisms can form classes; not limited to sets due to size concerns. |
| Faithfulness | Faithful forgetful functor to Set ensures concrete embedding. | No requirement for faithful embedding into Set or any small category. |
| Examples | Grp (groups), Top (topological spaces), Vect (vector spaces). | Category of all categories Cat, category of all sets Set. |
| Size | Usually locally small (hom-sets are sets), objects form a set or a small collection. | May be large or proper classes; hom-collections may be classes. |
Introduction to Concrete and Large Categories
Concrete categories are categories equipped with a faithful functor to the category of sets, enabling objects to be viewed as structured sets and morphisms as structure-preserving functions; this framework supports a tangible approach to categories through set theory. Large categories differ by potentially having proper classes of objects and morphisms rather than mere sets, which requires careful handling to avoid size paradoxes in category theory. Understanding the distinction between concrete and large categories is fundamental for applications in algebra, topology, and logic where the size and structural representation of categories impact both theory and practice.
Defining Concrete Categories
Concrete categories are defined by a faithful functor to the category of sets, allowing each object to be associated with an underlying set and morphisms to correspond to functions between these sets. This framework enables the study of algebraic or structured objects through their elements and operations, grounding abstract categorical concepts in more familiar set-theoretic terms. In contrast, large categories may lack such a faithful functor, emphasizing broader structural relations often beyond straightforward set-theoretic interpretation.
Understanding Large Categories
Large categories extend beyond the constraints of set size, allowing objects and morphisms to form classes too vast to be sets, contrasting with concrete categories that rely on underlying sets and structure-preserving functions. Understanding large categories involves grasping their role in higher-level category theory, where traditional set-based frameworks limit the scope, necessitating the use of proper classes to accommodate extensive collections like the category of all sets or all groups. This perspective enables advanced mathematical constructions and theories, embracing size universality while maintaining coherent categorical operations.
Key Differences Between Concrete and Large Categories
Concrete categories are mathematical structures equipped with a faithful functor to the category of sets, allowing elements within objects to be viewed as sets, whereas large categories are those with a proper class of objects or morphisms, often exceeding the size limitations of sets. The key difference lies in concrete categories having an underlying set structure that facilitates element-wise reasoning, while large categories emphasize size and scale without the necessity of a set-based framework. This distinction impacts their applications, with concrete categories often used in algebra and topology due to their set-theoretic nature, while large categories appear in higher category theory and foundations of mathematics.
Examples of Concrete Categories
Concrete categories are categories equipped with a faithful functor to the category of sets, enabling their objects to be viewed as sets with additional structure. Examples include the category of groups (Grp), where objects are groups with underlying sets and morphisms are group homomorphisms, the category of topological spaces (Top), consisting of spaces with continuous maps, and the category of vector spaces over a fixed field (Vect_k), featuring linear transformations between vector spaces. These categories contrast with large categories like Cat, the category of all small categories, which may not have a faithful set-valued functor and often involve higher-level abstract structures.
Examples of Large Categories
Large categories often include familiar mathematical structures such as the category of all sets (Set), the category of all groups (Grp), and the category of all topological spaces (Top), each consisting of a proper class of objects rather than a set. These examples illustrate how large categories encompass widely studied and foundational constructs in category theory that are too vast to form small categories. Understanding these large categories is crucial for advanced topics in algebra, topology, and logic where the size of the collections involved necessitates careful foundational handling.
Structural Properties and Size Considerations
Concrete categories possess a faithful functor to the category of sets, ensuring objects have underlying sets with structure-preserving morphisms, which allows direct manipulation of elements and facilitates construction of limits and colimits. Large categories, by contrast, encompass collections too vast to be sets but are proper classes, imposing foundational challenges and limiting certain constructions like small limits or representability within set-theoretic frameworks. Structural properties in concrete categories often leverage set-based intuition for factorization systems and adjunctions, while large categories require careful handling of size axioms and universes to maintain coherence and avoid paradoxes in categorical constructions.
Set-Theoretic Issues in Category Theory
Concrete categories are those equipped with a faithful functor to the category of sets, allowing objects and morphisms to be treated as sets and functions, which facilitates set-theoretic reasoning within category theory. Large categories, often too big to be sets themselves, pose foundational challenges because their collections of objects or morphisms form proper classes rather than sets, complicating naively applying set-theoretic methods. Addressing these issues requires careful use of Grothendieck universes or other foundational frameworks to avoid paradoxes and ensure rigorous treatment of large categories in a set-theoretic context.
Applications and Use Cases
Concrete categories, characterized by a faithful functor to the category of sets, find applications in computer science and algebra where underlying sets and explicit structures are crucial, such as in data type theory and automata. Large categories, often proper classes rather than sets, are essential in advanced mathematical fields like higher category theory and homotopy theory, enabling the study of vast collections of objects such as all small categories or functor categories. The distinction supports applications ranging from practical modeling in software engineering with concrete categories to foundational research in logic and topology involving large categories.
Conclusion: Choosing the Right Category
Selecting between concrete and large categories hinges on the specific requirements of structure and abstraction in a mathematical context. Concrete categories provide a tangible framework with sets and functions suited for practical, computational purposes. Large categories, often encompassing a broader scope and higher-level abstractions, are ideal for advanced theoretical explorations where size and complexity surpass set-based constraints.
Concrete category Infographic
 libterm.com
libterm.com