Non-amenable groups exhibit complex structures that defy the existence of an invariant mean, distinguishing them from amenable groups in group theory and functional analysis. These groups often arise in contexts involving paradoxical decompositions and have profound implications in geometry, probability, and operator algebras. Explore the rest of this article to deepen your understanding of non-amenable groups and their significant mathematical applications.
Table of Comparison
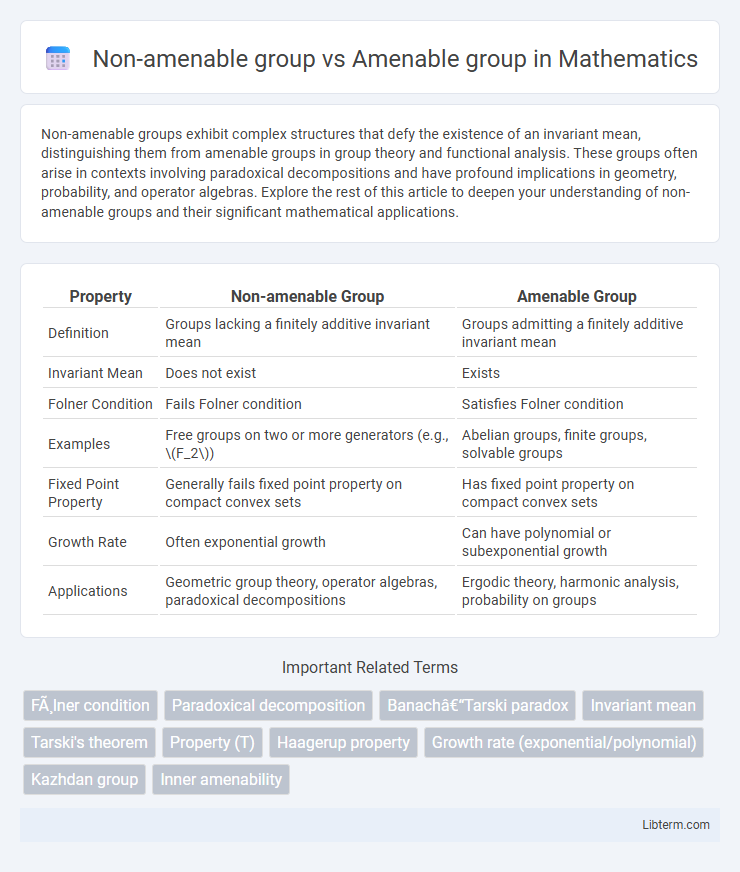
| Property | Non-amenable Group | Amenable Group |
|---|---|---|
| Definition | Groups lacking a finitely additive invariant mean | Groups admitting a finitely additive invariant mean |
| Invariant Mean | Does not exist | Exists |
| Folner Condition | Fails Folner condition | Satisfies Folner condition |
| Examples | Free groups on two or more generators (e.g., \(F_2\)) | Abelian groups, finite groups, solvable groups |
| Fixed Point Property | Generally fails fixed point property on compact convex sets | Has fixed point property on compact convex sets |
| Growth Rate | Often exponential growth | Can have polynomial or subexponential growth |
| Applications | Geometric group theory, operator algebras, paradoxical decompositions | Ergodic theory, harmonic analysis, probability on groups |
Introduction to Group Theory
Non-amenable groups are characterized by the absence of an invariant mean, contrasting with amenable groups where such a mean exists, allowing for a finitely additive, left-invariant measure on all subsets. In group theory, amenable groups include finite groups, abelian groups, and solvable groups, playing a crucial role in ergodic theory and harmonic analysis. Non-amenable groups often exhibit paradoxical decompositions and are fundamental in the study of geometric group theory and operator algebras.
Defining Amenable Groups
Amenable groups are defined by the existence of a finitely additive, translation-invariant probability measure on all of their subsets, reflecting a key property of measure theory and group actions. These groups admit Folner sequences, which are finite subsets whose boundaries become negligible compared to their size, illustrating their "averaging" behavior. In contrast, non-amenable groups lack such invariant means, often exhibiting paradoxical decompositions and correlating with properties like exponential growth or containing free subgroups.
Non-Amenable Groups: An Overview
Non-amenable groups lack an invariant mean, distinguishing them from amenable groups that possess a finitely additive, translation-invariant probability measure. Key examples of non-amenable groups include free groups on two or more generators and certain lattices in higher-rank Lie groups. Their properties have profound implications in geometric group theory, ergodic theory, and the study of von Neumann algebras, especially concerning paradoxical decompositions and the Banach-Tarski paradox.
Key Properties of Amenable Groups
Amenable groups are characterized by the existence of an invariant mean, which implies they satisfy the Folner condition, allowing finite subsets to approximate the group's behavior under translation. These groups exhibit properties such as closure under taking subgroups, quotients, and extensions, ensuring stability in various algebraic constructions. In contrast, non-amenable groups lack invariant means, leading to properties like paradoxical decompositions and the failure of the Banach-Tarski paradox, highlighting their more complex and less intuitive structure.
Distinct Features of Non-Amenable Groups
Non-amenable groups lack a finitely additive invariant probability measure, distinguishing them from amenable groups which possess such measures. They often exhibit properties like exponential growth, paradoxical decompositions, and failure to satisfy the Folner condition. These features lead to complex behaviors in ergodic theory and geometric group theory, making non-amenable groups central to the study of dynamical systems and operator algebras.
Historical Background and Development
The concept of amenable groups emerged in the 1920s with John von Neumann's work addressing the Banach-Tarski paradox, introducing amenability to distinguish groups allowing paradoxical decompositions. Non-amenable groups, characterized by the absence of an invariant mean, became central to geometric group theory and measured group theory developments in the mid-20th century. Subsequent research has deepened the understanding of amenability's connections to fixed point properties, ergodic theory, and operator algebras, highlighting its foundational role in modern group theory.
Examples of Amenable vs. Non-Amenable Groups
Amenable groups, such as abelian groups like \(\mathbb{Z}\) (the integers under addition) and finite groups, possess an invariant mean facilitating averaging processes, while non-amenable groups like free groups on two or more generators (e.g., the free group \(F_2\)) lack this property due to their exponential growth and paradoxical decompositions. Solvable groups and compact groups are classic examples of amenable groups, whereas groups containing a free subgroup on two generators exemplify non-amenable structures, reflecting highly non-trivial dynamics and geometric properties. The contrast between amenable and non-amenable groups manifests in areas like ergodic theory, geometric group theory, and operator algebras, notably impacting fixed-point theorems and growth behaviors.
Importance in Mathematics and Applications
Non-amenable groups, characterized by their inability to support invariant means, play a crucial role in understanding phenomena like paradoxical decompositions and rigidity properties in geometric group theory. Amenable groups, defined by the existence of invariant finitely additive measures, are fundamental in ergodic theory, harmonic analysis, and probability, facilitating the study of averaging processes and fixed point theorems. The distinction impacts applications ranging from statistical mechanics and operator algebras to network theory and dynamical systems, where amenability dictates behavior and structural properties crucial for both theoretical insights and practical modeling.
Open Problems and Recent Research
Non-amenable groups exhibit complex behavior in geometric group theory, with open problems centered around characterizing their boundaries and growth rates, particularly in non-exact groups and groups with intermediate growth. Recent research explores connections between non-amenability, property (T), and the Baum-Connes conjecture, analyzing their implications for operator algebras and rigidity phenomena. Progress in understanding amenable groups emphasizes classification results in solvable and elementary amenable classes, while challenges remain in determining amenability for specific groups arising from dynamical systems and random walks.
Conclusion and Future Directions
Non-amenable groups exhibit complex behaviors such as paradoxical decompositions and lack of invariant means, contrasting with amenable groups that possess fixed points and Folner sequences. The study of non-amenable groups continues to impact fields like geometric group theory, operator algebras, and ergodic theory by providing insights into rigidity phenomena and growth rates. Future research aims to explore new invariants, classify broader families of groups, and develop applications in quantum computing and topological dynamics.
Non-amenable group Infographic
 libterm.com
libterm.com