The kernel is the core component of an operating system responsible for managing hardware resources and facilitating communication between software and hardware. It controls system processes, memory allocation, and device management to ensure efficient and secure operation. Explore the rest of the article to understand how the kernel impacts your computer's performance and security.
Table of Comparison
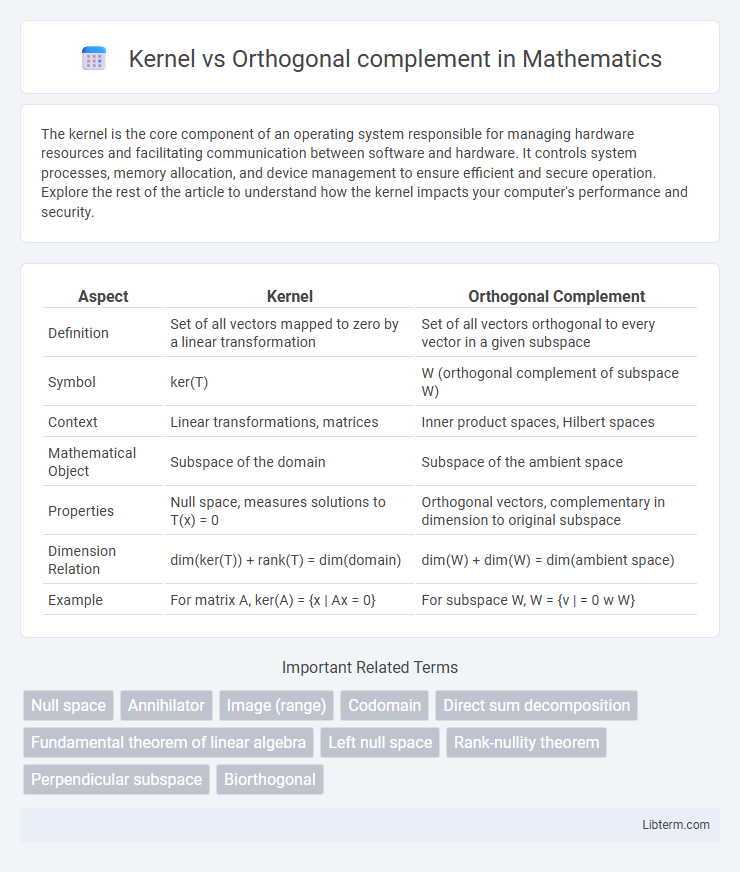
| Aspect | Kernel | Orthogonal Complement |
|---|---|---|
| Definition | Set of all vectors mapped to zero by a linear transformation | Set of all vectors orthogonal to every vector in a given subspace |
| Symbol | ker(T) | W (orthogonal complement of subspace W) |
| Context | Linear transformations, matrices | Inner product spaces, Hilbert spaces |
| Mathematical Object | Subspace of the domain | Subspace of the ambient space |
| Properties | Null space, measures solutions to T(x) = 0 | Orthogonal vectors, complementary in dimension to original subspace |
| Dimension Relation | dim(ker(T)) + rank(T) = dim(domain) | dim(W) + dim(W) = dim(ambient space) |
| Example | For matrix A, ker(A) = {x | Ax = 0} | For subspace W, W = {v | |
Introduction to Kernel and Orthogonal Complement
The kernel of a linear transformation is the set of all vectors mapped to the zero vector, representing the solution space of the homogeneous equation associated with the transformation. The orthogonal complement of a subspace consists of all vectors orthogonal to every vector in that subspace, forming a critical tool in decomposing vector spaces. Understanding these concepts aids in analyzing linear systems and vector space structure, especially in inner product spaces.
Understanding Vector Spaces and Subspaces
The kernel of a linear transformation is the set of all vectors that map to the zero vector, revealing key information about the transformation's nullity and the structure of vector spaces. The orthogonal complement of a subspace consists of all vectors orthogonal to every vector in the original subspace, playing a crucial role in understanding projections and dimensions within inner product spaces. Together, the kernel and orthogonal complement help analyze subspace relations, rank-nullity theorem applications, and the decomposition of vector spaces.
Defining the Kernel in Linear Algebra
The kernel of a linear transformation is the set of all vectors mapped to the zero vector, forming a subspace that measures the transformation's nullity. It consists of solutions to the homogeneous equation \(T(\mathbf{x}) = \mathbf{0}\), where \(T\) is a linear map between vector spaces. Understanding the kernel is crucial for analyzing the structure of the transformation and its relationship with the orthogonal complement of its image.
Exploring the Orthogonal Complement Concept
The orthogonal complement of a subspace in a vector space consists of all vectors that are orthogonal to every vector in the original subspace, highlighting a fundamental relationship between geometric and algebraic structures. Unlike the kernel, which is the set of vectors mapped to the zero vector by a linear transformation, the orthogonal complement emphasizes perpendicularity and can be used to decompose spaces into direct sums. Exploring the orthogonal complement concept is crucial in understanding projections, solving linear systems, and analyzing eigenvalues in spaces with inner products.
Geometric Interpretation: Kernel vs Orthogonal Complement
The kernel of a linear transformation consists of all vectors mapped to the zero vector, representing directions collapsed onto the origin, while the orthogonal complement of a subspace contains all vectors orthogonal to every vector in that subspace. Geometrically, the kernel corresponds to the null space where the transformation loses dimension, and the orthogonal complement forms a subspace perpendicular to the given set, highlighting duality in vector spaces. For example, in Euclidean space, the kernel relates to points flattened to zero under a matrix, whereas the orthogonal complement defines the space of vectors perpendicular to the image or column space.
Key Differences Between Kernel and Orthogonal Complement
The kernel of a linear transformation consists of all vectors mapped to the zero vector, representing solutions to homogeneous equations, while the orthogonal complement contains vectors orthogonal to a given subspace, defining a perpendicular space in inner product spaces. The kernel is a subspace characterized by the nullity of the transformation, essential in determining linear dependence and rank-nullity theorem applications, whereas the orthogonal complement directly relates to projections and decomposition in Euclidean spaces. Key differences include their role: kernel identifies vectors annihilated by a linear map, while the orthogonal complement defines the space of vectors orthogonal to another subspace, influencing methods in linear algebra, functional analysis, and signal processing.
Applications in Mathematics and Engineering
The kernel of a linear transformation represents the set of all vectors mapped to the zero vector, crucial for solving systems of linear equations and determining linear independence in mathematics. The orthogonal complement, defined as the set of all vectors orthogonal to a given subspace, plays a vital role in projection methods, signal processing, and error correction codes in engineering. Both concepts underpin dimensionality reduction techniques and stability analysis in control systems, highlighting their interdisciplinary importance.
The Role in Solving Linear Systems
The kernel of a linear transformation represents all vectors mapped to the zero vector, directly corresponding to the solution set of the homogeneous system Ax = 0, indicating the degrees of freedom in the solution space. The orthogonal complement relates to the space of vectors that are perpendicular to the image of the linear transformation, playing a critical role in characterizing constraints and ensuring the consistency of non-homogeneous systems Ax = b by verifying whether b lies in the image of A. Understanding both kernel and orthogonal complements is essential for determining solution existence and uniqueness in linear algebra and computational methods.
Examples and Visualizations
The kernel of a matrix consists of all vectors mapped to zero, such as the solution set of Ax = 0, visualized as a null space line or plane within the input space. The orthogonal complement comprises all vectors perpendicular to a given subspace, easily represented by vectors orthogonal to a plane or line in Euclidean space. For example, in R3, the kernel of a 3x3 matrix with rank 2 forms a line through the origin, while its orthogonal complement forms a plane orthogonal to that line, illustrating the dual geometric nature of these concepts.
Conclusion: Choosing the Right Concept
Selecting between the kernel and orthogonal complement depends on the linear algebra problem at hand; the kernel provides insight into the solution space of a linear transformation by identifying vectors mapped to zero. The orthogonal complement offers a way to understand subspace relationships and projections by involving vectors orthogonal to a given subspace. Understanding the context--whether analyzing null spaces or decomposing vector spaces--guides the choice for optimal problem-solving strategies.
Kernel Infographic
 libterm.com
libterm.com