Constructive feedback focuses on providing clear, specific, and actionable suggestions that foster growth and improvement. It aims to highlight strengths while addressing areas that need development in a respectful and supportive manner. Discover how constructive approaches can transform challenges into opportunities by reading the rest of the article.
Table of Comparison
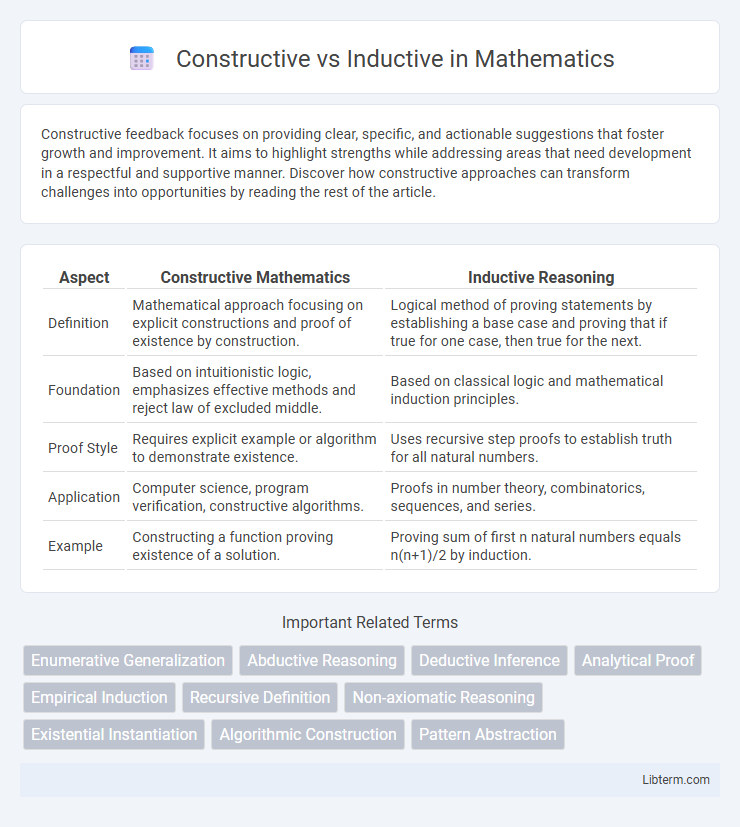
| Aspect | Constructive Mathematics | Inductive Reasoning |
|---|---|---|
| Definition | Mathematical approach focusing on explicit constructions and proof of existence by construction. | Logical method of proving statements by establishing a base case and proving that if true for one case, then true for the next. |
| Foundation | Based on intuitionistic logic, emphasizes effective methods and reject law of excluded middle. | Based on classical logic and mathematical induction principles. |
| Proof Style | Requires explicit example or algorithm to demonstrate existence. | Uses recursive step proofs to establish truth for all natural numbers. |
| Application | Computer science, program verification, constructive algorithms. | Proofs in number theory, combinatorics, sequences, and series. |
| Example | Constructing a function proving existence of a solution. | Proving sum of first n natural numbers equals n(n+1)/2 by induction. |
Understanding Constructive and Inductive Approaches
Constructive approaches emphasize building knowledge through concrete examples and step-by-step problem-solving, fostering deeper comprehension by actively creating solutions. Inductive approaches rely on observing patterns and deriving general principles from specific instances, enabling learners to formulate broader concepts through experience. Both methods enhance understanding by engaging learners differently: constructive focuses on building knowledge structures, while inductive emphasizes pattern recognition and generalization.
Key Definitions and Concepts
Constructive reasoning builds mathematical objects explicitly, providing concrete examples or algorithms that demonstrate existence, while inductive reasoning establishes general truths by proving a base case and a stepwise progression. Constructive proofs emphasize the creation of entities, ensuring that existence claims are backed by explicit construction, whereas inductive proofs rely on the principle of mathematical induction to confirm properties across infinite sequences or structures. Understanding these key concepts is crucial for distinguishing between proof strategies in logic and mathematics, impacting areas such as computer science and formal verification.
Historical Background and Evolution
Constructive reasoning originated from early mathematical foundations emphasizing explicit construction of objects, notably formalized during the development of intuitionistic logic by L.E.J. Brouwer in the early 20th century. Inductive reasoning, rooted in Aristotle's empirical observations and later formalized through the scientific method, evolved as a fundamental approach to generalizing from specific cases to broader principles. Over time, constructive logic has influenced computer science and proof theory, while inductive methods remain central to empirical sciences and machine learning algorithms.
Fundamental Differences: Constructive vs Inductive
Constructive reasoning involves building a concrete example or algorithm to prove the existence of a mathematical object, emphasizing explicit construction. Inductive reasoning establishes the truth of infinitely many cases by proving a base case and a general inductive step, relying on a logical progression rather than explicit examples. The fundamental difference lies in constructive proofs providing tangible instances, while inductive proofs guarantee truth through structural patterns and recurrence relations.
Methods of Reasoning: Step-by-Step Comparison
Constructive reasoning establishes the existence of a mathematical object by explicitly providing it, while inductive reasoning infers a general rule from specific cases through repeated observations. Constructive methods rely on building examples or algorithms step-by-step, ensuring a direct proof, whereas inductive methods use a base case and an inductive step to prove statements for all natural numbers. In summary, constructive reasoning produces tangible evidence, and inductive reasoning validates propositions via a logical progression from particular instances.
Applications in Research and Academics
Constructive methods play a crucial role in research and academics by providing explicit examples or algorithms that demonstrate the existence of mathematical objects, enhancing practical understanding and application in fields like computer science and algebra. Inductive reasoning is fundamental in formulating general hypotheses and theories from specific observations, widely employed in scientific research to develop models and validate empirical data. Both approaches complement each other by ensuring theoretical rigor and empirical relevance across disciplines such as mathematics, physics, and social sciences.
Advantages and Limitations of Each Approach
Constructive reasoning provides explicit examples or constructions, ensuring that mathematical objects are verifiable and computationally realizable, which benefits algorithm design and formal proofs; however, it can be limited by its inherently restrictive framework that excludes non-constructive existence proofs. Inductive reasoning excels in establishing properties over infinite structures like natural numbers by proving base cases and inductive steps, offering broad applicability in mathematics and computer science, but it may struggle with non-well-founded or highly complex systems where induction hypotheses are difficult to formulate or apply. The choice between constructive and inductive approaches depends on the need for explicit constructibility versus generalizability in proof methodology.
Case Studies: Constructive and Inductive in Practice
Constructive case studies emphasize building detailed frameworks or prototypes, showcasing how theoretical models are applied to create practical solutions. Inductive case studies analyze patterns from qualitative data to develop broader generalizations or theories grounded in real-world observations. Both methods provide valuable insights: constructive case studies demonstrate application effectiveness, while inductive case studies deepen understanding through emergent themes.
Choosing the Right Approach for Your Needs
Choosing the right approach between constructive and inductive methods depends on your specific goals and the nature of the problem at hand. Constructive methods provide explicit solutions or algorithms, ideal for scenarios requiring direct implementation or verification, while inductive approaches rely on pattern recognition and generalization, best suited for exploratory analysis and hypothesis generation. Evaluating the complexity, desired rigor, and application context helps determine whether a constructive or inductive strategy optimally addresses your needs.
Future Trends in Constructive and Inductive Reasoning
Future trends in constructive and inductive reasoning emphasize the integration of artificial intelligence and machine learning to enhance problem-solving capabilities in dynamic environments. Advances in computational logic and probabilistic models are driving more efficient and scalable methods for constructing proofs and generating hypotheses from incomplete data. Research is increasingly focused on hybrid approaches that combine the rigor of constructive methods with the flexibility of inductive reasoning to address complex real-world challenges.
Constructive Infographic
 libterm.com
libterm.com