Separable space is a fundamental concept in topology characterized by the existence of a countable dense subset. This property ensures that the space is manageable in terms of approximation and analysis, making it essential in functional analysis and related fields. Discover how separable spaces influence your understanding of complex topological structures by reading the rest of this article.
Table of Comparison
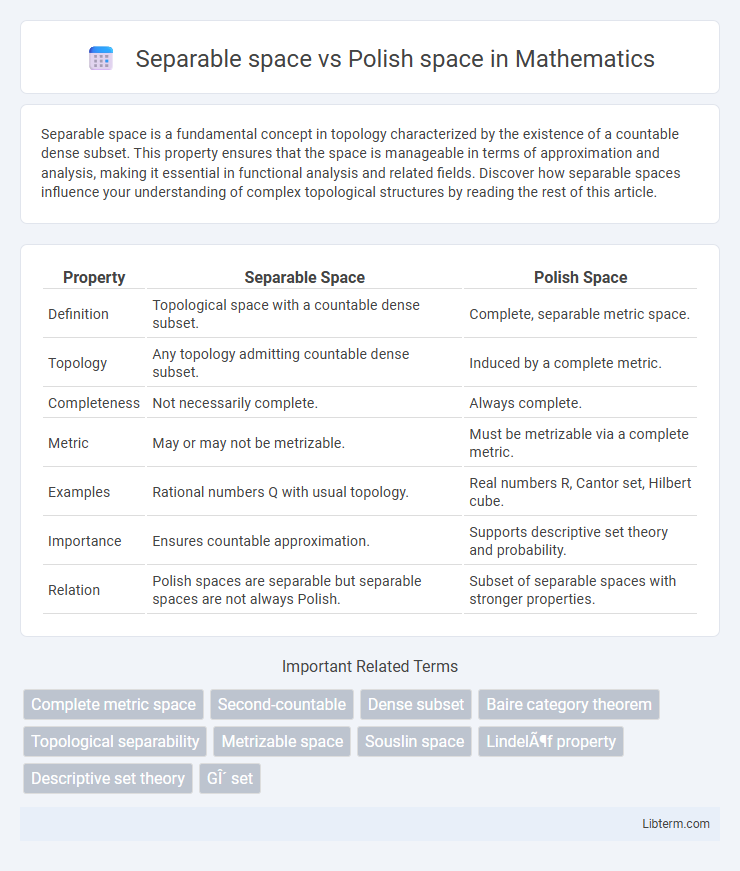
| Property | Separable Space | Polish Space |
|---|---|---|
| Definition | Topological space with a countable dense subset. | Complete, separable metric space. |
| Topology | Any topology admitting countable dense subset. | Induced by a complete metric. |
| Completeness | Not necessarily complete. | Always complete. |
| Metric | May or may not be metrizable. | Must be metrizable via a complete metric. |
| Examples | Rational numbers Q with usual topology. | Real numbers R, Cantor set, Hilbert cube. |
| Importance | Ensures countable approximation. | Supports descriptive set theory and probability. |
| Relation | Polish spaces are separable but separable spaces are not always Polish. | Subset of separable spaces with stronger properties. |
Introduction to Separable and Polish Spaces
Separable spaces are topological spaces containing a countable dense subset, making them crucial in analysis and topology for simplifying complex structures through countable approximations. Polish spaces are separable completely metrizable spaces, meaning they admit a metric with respect to which they are complete and have a countable dense subset, facilitating powerful descriptive set theory and measure theory applications. Understanding the distinction between separability and complete metrizability is essential for grasping how Polish spaces extend the concept of separable spaces with stronger structural properties.
Defining Separable Spaces
A separable space is a topological space containing a countable, dense subset, meaning the closure of this subset equals the entire space. This property ensures separable spaces have manageable complexity, enabling easier approximation and analysis in areas like functional analysis and metric space theory. In contrast, Polish spaces are separable complete metric spaces, combining separability with completeness to support robust topological and measure-theoretic structures.
Understanding Polish Spaces
Polish spaces are complete separable metric spaces characterized by their rich topological structure, making them a fundamental object of study in descriptive set theory and analysis. Every Polish space is separable, meaning it contains a countable dense subset, but not every separable space is Polish, as completeness is required. Understanding Polish spaces involves grasping properties like separability, completeness, and metric compatibility, which enable powerful results such as the Baire category theorem and universal measurability.
Key Properties of Separable Spaces
Separable spaces are topological spaces containing a countable dense subset, which ensures the space is second countable and metrizable under certain conditions. Unlike Polish spaces, which are complete separable metric spaces, separable spaces do not require completeness, allowing more generality but fewer guarantees of structure. Key properties include the hereditary separability of subspaces and the preservation of separability under continuous images and countable products, making separable spaces fundamental in analysis and topology.
Essential Features of Polish Spaces
Polish spaces are complete, separable metric spaces characterized by their ability to support a compatible complete metric, ensuring convergence of Cauchy sequences within the space. Unlike general separable spaces, Polish spaces possess a richer topological structure, enabling extensive applications in descriptive set theory and probability. Their essential features include second countability, metrizability, and the property of being a Gd subset in their completion.
Differences Between Separable and Polish Spaces
Separable spaces contain a countable dense subset, ensuring that every point in the space can be approximated arbitrarily closely by elements from this countable set. Polish spaces are separable completely metrizable topological spaces, meaning they not only have a countable dense subset but also admit a complete metric inducing their topology. The key difference lies in completeness: all Polish spaces are separable, but not all separable spaces are Polish due to potential lack of a compatible complete metric.
Relationship Between Separable and Polish Spaces
A Polish space is a separable completely metrizable topological space, meaning every Polish space is inherently separable but with the additional property of complete metrizability. Conversely, separable spaces lack the completeness requirement, making them a broader category that includes Polish spaces as a subclass. The key relationship is that while all Polish spaces are separable, not all separable spaces qualify as Polish due to potential absence of a complete metric.
Examples of Separable but Non-Polish Spaces
An example of a separable but non-Polish space is the space of rationals \(\mathbb{Q}\) with the usual metric inherited from \(\mathbb{R}\); it is countable and dense in itself but not complete, hence not Polish. Another case includes certain metric spaces like the Sorgenfrey line, which is separable due to countability of rational points but lacks a complete metric structure, preventing it from being Polish. Spaces that are separable metric spaces but fail to be completely metrizable serve as classic examples distinguishing separability from the Polish property.
Applications of Separable and Polish Spaces
Separable spaces, characterized by the existence of a countable dense subset, are essential in functional analysis and probability theory, facilitating the study of convergence and measurability properties. Polish spaces, defined as completely metrizable separable spaces, play a critical role in descriptive set theory, dynamical systems, and ergodic theory by providing a robust framework for analyzing Borel hierarchies and invariant measures. Applications of separable and Polish spaces extend to machine learning, where their topological structure enables effective algorithms for pattern recognition and statistical inference in infinite-dimensional settings.
Summary and Key Takeaways
Separable spaces are topological spaces that contain a countable dense subset, which simplifies analysis by enabling approximation through countable elements. Polish spaces are a subclass of separable spaces characterized by being completely metrizable and topologically complete, providing a robust framework for descriptive set theory and probability. Key takeaways include that all Polish spaces are separable, but not all separable spaces are Polish, highlighting the importance of metrizability and completeness in advanced topological analysis.
Separable space Infographic
 libterm.com
libterm.com