A groupoid is an algebraic structure generalizing groups by allowing partial binary operations that are only defined for certain pairs of elements rather than all. It plays a crucial role in category theory and topology, modeling symmetry and transformations where operations are not globally applicable. Explore the rest of the article to understand how groupoids are used in mathematics and their applications in various fields.
Table of Comparison
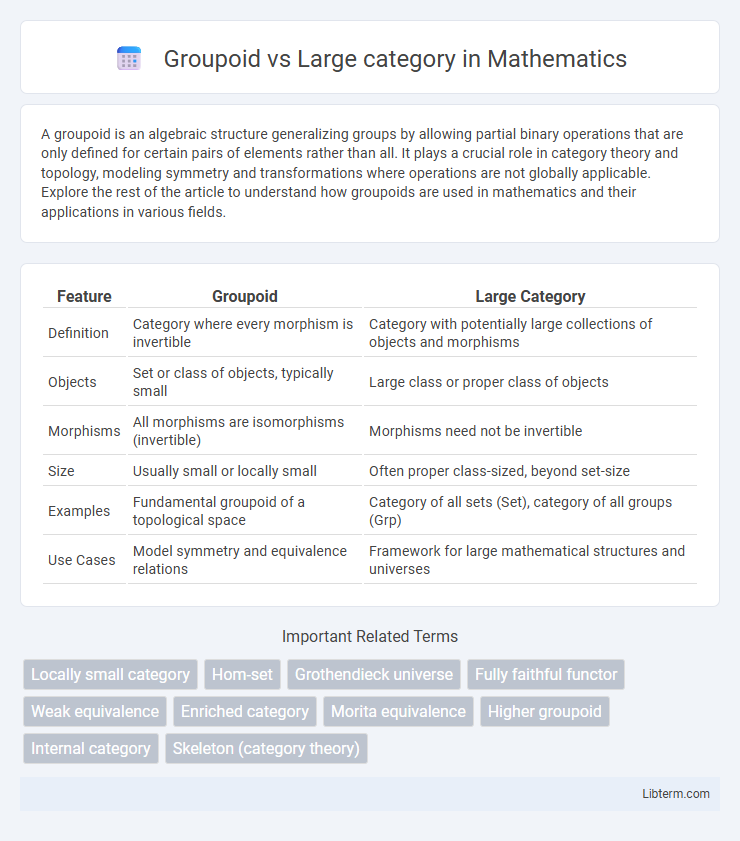
| Feature | Groupoid | Large Category |
|---|---|---|
| Definition | Category where every morphism is invertible | Category with potentially large collections of objects and morphisms |
| Objects | Set or class of objects, typically small | Large class or proper class of objects |
| Morphisms | All morphisms are isomorphisms (invertible) | Morphisms need not be invertible |
| Size | Usually small or locally small | Often proper class-sized, beyond set-size |
| Examples | Fundamental groupoid of a topological space | Category of all sets (Set), category of all groups (Grp) |
| Use Cases | Model symmetry and equivalence relations | Framework for large mathematical structures and universes |
Introduction to Groupoids and Large Categories
Groupoids generalize groups by allowing partial symmetries encoded as invertible morphisms between objects, where every morphism has an inverse, forming a category with all arrows invertible. Large categories, often defined to handle collections too big to be sets, encompass both small categories and structures like groupoids, accounting for entities whose objects and morphisms form classes rather than sets. Understanding the distinction highlights that groupoids are a type of category emphasizing invertible morphisms, while large categories address foundational size issues important in category theory and higher-level mathematical frameworks.
Fundamental Definitions: Groupoid vs Large Category
A groupoid is a category where every morphism is invertible, emphasizing symmetry and equivalence relations within mathematical structures. In contrast, a large category is characterized by having a class of objects and morphisms that may not form a set, allowing for more extensive collections beyond set-theoretic constraints. The fundamental distinction lies in the invertibility of morphisms for groupoids versus the potential infinitude and generality of objects and morphisms in large categories.
Historical Context and Development
Groupoids originated in the early 20th century as algebraic structures generalizing groups by allowing partial symmetries, first studied extensively by Heinrich Brandt in 1926. Large categories emerged later with the formalization of category theory by Eilenberg and Mac Lane in the 1940s, providing a framework to handle collections of objects and morphisms that could be too big to form sets within traditional set theory. The evolution from groupoids to large categories reflects the expanding scope in abstract algebra and topology, enabling mathematicians to address increasingly complex structures and foundational issues.
Structural Properties and Key Differences
Groupoids are categories where every morphism is invertible, emphasizing symmetry and equivalence relations within their structure. Large categories can have morphisms without inverses, allowing for more general and hierarchical relationships beyond equivalences. The key difference lies in groupoids' strict invertibility constraint, which imparts a group-like structure to objects, whereas large categories accommodate broader morphism compositions without requiring invertibility.
Examples of Groupoids in Mathematics
Groupoids are algebraic structures generalizing groups by allowing partial binary operations defined only on compatible pairs, exemplified by the fundamental groupoid in algebraic topology, which encodes homotopy classes of paths between points in a space. Unlike large categories that may have morphisms between disparate objects without invertibility, groupoids require every morphism to be invertible, making them central in representing symmetries and equivalences in mathematical contexts such as Lie groupoids in differential geometry and groupoid schemes in algebraic geometry. These examples highlight how groupoids provide a flexible framework for studying local symmetries and equivalence relations that large categories might not inherently capture.
Illustrative Cases of Large Categories
Large categories often feature a class-sized collection of objects and morphisms, which contrasts with groupoids that have invertible morphisms limited to sets. Illustrative cases of large categories include the category of all sets (Set), the category of all topological spaces (Top), and the category of all groups (Grp), each representing a proper class rather than a set. These examples highlight how large categories extend beyond the scope of groupoids by encompassing vast structures with non-invertible morphisms and multi-level compositional complexity.
Role in Category Theory
Groupoids serve as categories where every morphism is invertible, emphasizing symmetry and equivalence relations within category theory. Large categories, characterized by having classes rather than sets of objects and morphisms, provide a foundational framework for studying mathematical structures too extensive to be sets. The role of groupoids in category theory highlights local symmetries and homotopy types, while large categories facilitate the handling of universes and foundational hierarchies in higher-category theory.
Applications in Modern Mathematics
Groupoids provide versatile frameworks for modeling symmetries and equivalence relations in topology, algebraic geometry, and mathematical physics, especially in studying fundamental groups and orbifolds. Large categories, encompassing vast collections of objects and morphisms, are essential in category theory and homotopy theory for handling universes and the foundations of higher-dimensional algebra. Both structures facilitate advanced applications such as stack theory, descent theory, and the formalization of generalized cohomology theories.
Comparative Advantages and Limitations
Groupoids provide a flexible framework for modeling symmetries and equivalences by allowing every morphism to be invertible, which simplifies the analysis of isomorphism classes and homotopy types. Large categories, encompassing more diverse and possibly non-invertible morphisms, enable broader mapping structures necessary for complex algebraic or topological constructions but may introduce higher complexity in handling morphism compositions and limits. The invertibility constraint in groupoids limits their expressiveness compared to large categories, while large categories' relaxed conditions can complicate categorical coherence and equivalence reasoning.
Summary and Future Perspectives
Groupoids generalize groups by allowing partial symmetries and invertible morphisms between objects, while large categories encompass extensive collections of objects and morphisms without limitations on size. The study of groupoids enriches algebraic topology and category theory by enabling refined symmetry analyses, whereas large categories facilitate the handling of complex mathematical structures beyond set-theoretic constraints. Future research aims to deepen the integration of groupoid theory with higher category theory and explore applications in homotopy theory, quantum algebra, and mathematical physics to address foundational problems in these domains.
Groupoid Infographic
 libterm.com
libterm.com