Non-Archimedean analysis explores mathematical structures where the traditional Archimedean property does not hold, focusing on fields equipped with non-Archimedean valuations such as p-adic numbers. This branch of analysis offers unique insights into number theory and algebraic geometry by studying continuity, convergence, and differentiation under these alternative metrics. Discover how Non-Archimedean analysis can deepen your understanding of modern mathematical frameworks by reading the rest of the article.
Table of Comparison
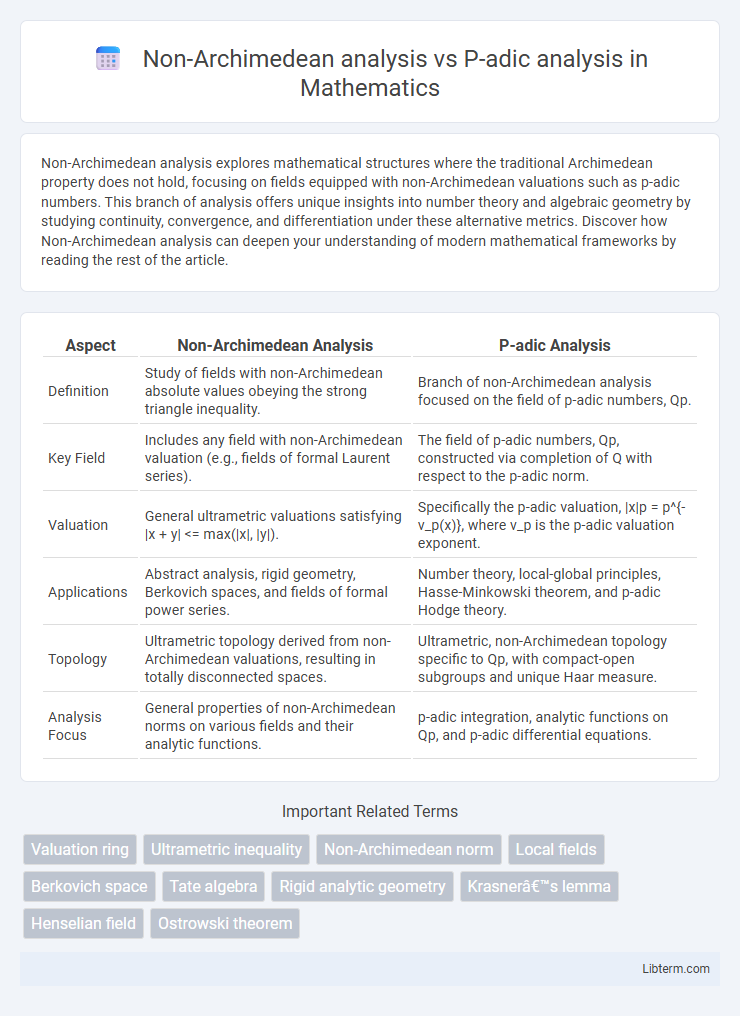
| Aspect | Non-Archimedean Analysis | P-adic Analysis |
|---|---|---|
| Definition | Study of fields with non-Archimedean absolute values obeying the strong triangle inequality. | Branch of non-Archimedean analysis focused on the field of p-adic numbers, Qp. |
| Key Field | Includes any field with non-Archimedean valuation (e.g., fields of formal Laurent series). | The field of p-adic numbers, Qp, constructed via completion of Q with respect to the p-adic norm. |
| Valuation | General ultrametric valuations satisfying |x + y| <= max(|x|, |y|). | Specifically the p-adic valuation, |x|p = p^{-v_p(x)}, where v_p is the p-adic valuation exponent. |
| Applications | Abstract analysis, rigid geometry, Berkovich spaces, and fields of formal power series. | Number theory, local-global principles, Hasse-Minkowski theorem, and p-adic Hodge theory. |
| Topology | Ultrametric topology derived from non-Archimedean valuations, resulting in totally disconnected spaces. | Ultrametric, non-Archimedean topology specific to Qp, with compact-open subgroups and unique Haar measure. |
| Analysis Focus | General properties of non-Archimedean norms on various fields and their analytic functions. | p-adic integration, analytic functions on Qp, and p-adic differential equations. |
Introduction to Non-Archimedean Analysis
Non-Archimedean analysis studies mathematical structures where the usual Archimedean property does not hold, often involving ultrametric spaces with strong triangle inequality. P-adic analysis is a prominent example of Non-Archimedean analysis, focusing on fields of p-adic numbers equipped with a valuation satisfying the non-Archimedean norm. The introduction to Non-Archimedean analysis emphasizes the topology and algebra of non-Archimedean fields, enabling unique convergence properties and applications in number theory and algebraic geometry.
Fundamentals of P-adic Analysis
P-adic analysis is a branch of non-Archimedean analysis that studies the properties of functions and series over p-adic number fields, which are complete with respect to the p-adic valuation. Fundamentals of p-adic analysis involve understanding ultrametric spaces, the unique topology induced by the p-adic norm, and convergence criteria distinct from real analysis. Key concepts include p-adic integers, valuation rings, and continuity defined through the non-Archimedean absolute value, which leads to novel insights in number theory and algebraic geometry.
Non-Archimedean vs Archimedean Valuations
Non-Archimedean analysis studies spaces equipped with a valuation satisfying the strong triangle inequality, leading to ultrametric properties, while Archimedean valuations, like the usual absolute value on real numbers, obey the standard triangle inequality. P-adic analysis is a prominent example of Non-Archimedean analysis, utilizing p-adic valuations that assign size based on divisibility by a prime p, creating a field with discrete, non-Archimedean valuation. The fundamental difference lies in valuation behavior: Non-Archimedean valuations ensure that the distance between points does not exceed the maximum of individual distances, contrasting with Archimedean valuations, which allow for additive distance accumulation.
Key Differences Between Non-Archimedean and P-adic Analysis
Non-Archimedean analysis studies mathematical structures defined over fields with non-Archimedean absolute values, emphasizing general properties of ultrametric spaces and valuation theory. P-adic analysis is a specialized branch within non-Archimedean analysis focused on the field of p-adic numbers, utilizing their unique algebraic and topological properties for number theory and arithmetic geometry. Key differences include the scope of application, where non-Archimedean analysis applies to a broad class of fields, while p-adic analysis targets the complete fields with respect to the p-adic norm, and methodological focus, with p-adic analysis leveraging explicit valuations tied to prime numbers.
Topological Properties in Non-Archimedean Fields
Non-Archimedean analysis studies fields endowed with a non-Archimedean valuation, leading to an ultrametric topology where open balls are both open and closed, producing a totally disconnected, locally compact topological space. P-adic analysis is a specific case of Non-Archimedean analysis focused on p-adic number fields \(\mathbb{Q}_p\), whose topological properties include completeness, compactness of the unit ball, and a basis composed of clopen sets. The discrete valuation in p-adic fields induces a strong triangle inequality that fundamentally shapes continuity, convergence, and differentiability within Non-Archimedean topologies.
P-adic Numbers: Construction and Properties
P-adic numbers are constructed using a completion of the rational numbers with respect to the p-adic norm, which measures distance based on divisibility by a fixed prime p. Unlike real numbers, p-adic numbers exhibit a non-Archimedean absolute value that satisfies the ultrametric inequality, leading to unique properties such as open and closed balls coinciding. This structure enables applications in number theory and algebraic geometry, where local fields and continuous functions are analyzed within the p-adic framework.
Applications of Non-Archimedean Analysis
Non-Archimedean analysis, a broad field encompassing P-adic analysis, is crucial in number theory, algebraic geometry, and dynamical systems where ultrametric spaces provide unique structural insights. Applications include solving Diophantine equations, modeling hierarchical data structures, and optimizing algorithms in cryptography through the manipulation of non-Archimedean norms. Its frameworks extend to recent advances in p-adic Hodge theory and rigid analytic spaces, facilitating deeper understanding of arithmetic schemes and modular forms.
Historical Development of P-adic and Non-Archimedean Analysis
P-adic analysis, originating from Kurt Hensel's introduction of p-adic numbers in 1897, laid the foundational framework for non-Archimedean analysis by extending classical analysis concepts to fields equipped with non-Archimedean valuations. The historical development of non-Archimedean analysis expanded these ideas beyond p-adic numbers, incorporating broader valuation theory and ultrametric spaces, influenced by works of mathematicians like Ostrowski and Krasner. This evolution bridged number theory and topology, enabling profound insights into algebraic and arithmetic geometry through the rigorous study of spaces with non-Archimedean norms.
Interconnections and Overlaps in Theories
Non-Archimedean analysis and p-adic analysis both explore mathematical structures characterized by non-Archimedean absolute values, with p-adic analysis specifically centered on fields equipped with p-adic valuations. Theories in these areas overlap significantly, particularly in studying ultrametric spaces where the strong triangle inequality holds, enabling insights into convergence, continuity, and analytic functions over non-Archimedean fields. Interconnections are evident in applications such as rigid analytic geometry and number theory, where p-adic methods serve as specialized instances of broader non-Archimedean analytic frameworks.
Future Directions in Non-Archimedean and P-adic Research
Non-Archimedean analysis and p-adic analysis increasingly influence advancements in number theory, algebraic geometry, and mathematical physics through their unique ultrametric topologies and valuation-based frameworks. Future research directions emphasize the development of non-Archimedean functional analysis, exploring new applications in p-adic differential equations, dynamical systems, and potential impacts on quantum computing algorithms. Emerging interdisciplinary studies aim to deepen understanding of Berkovich spaces and their role in tropical geometry, fostering novel computational tools and theoretical foundations within non-Archimedean contexts.
Non-Archimedean analysis Infographic
 libterm.com
libterm.com