Singular homology is a fundamental concept in algebraic topology that assigns a sequence of abelian groups or modules to a topological space, capturing its essential geometric features. It uses singular simplices, continuous maps from standard simplices to the space, to build chain complexes whose homology groups reveal information about holes and connectivity. Explore the article to deepen your understanding of how singular homology provides powerful tools for classifying topological spaces.
Table of Comparison
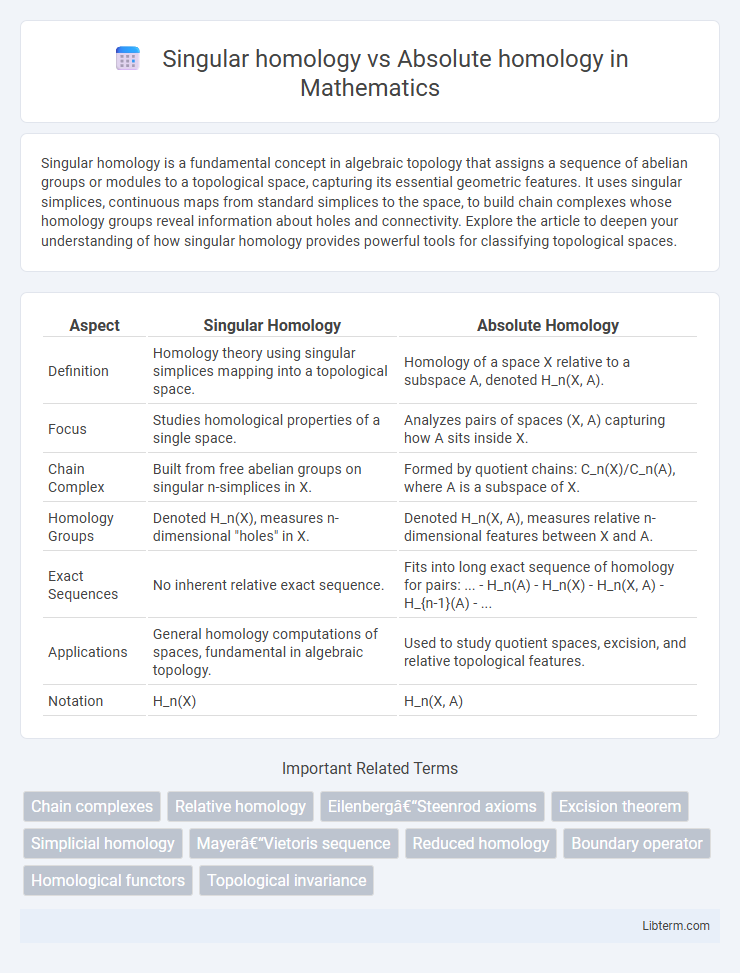
| Aspect | Singular Homology | Absolute Homology |
|---|---|---|
| Definition | Homology theory using singular simplices mapping into a topological space. | Homology of a space X relative to a subspace A, denoted H_n(X, A). |
| Focus | Studies homological properties of a single space. | Analyzes pairs of spaces (X, A) capturing how A sits inside X. |
| Chain Complex | Built from free abelian groups on singular n-simplices in X. | Formed by quotient chains: C_n(X)/C_n(A), where A is a subspace of X. |
| Homology Groups | Denoted H_n(X), measures n-dimensional "holes" in X. | Denoted H_n(X, A), measures relative n-dimensional features between X and A. |
| Exact Sequences | No inherent relative exact sequence. | Fits into long exact sequence of homology for pairs: ... - H_n(A) - H_n(X) - H_n(X, A) - H_{n-1}(A) - ... |
| Applications | General homology computations of spaces, fundamental in algebraic topology. | Used to study quotient spaces, excision, and relative topological features. |
| Notation | H_n(X) | H_n(X, A) |
Introduction to Homology Theories
Singular homology serves as a foundational tool in algebraic topology by associating a sequence of abelian groups or modules to a topological space using continuous maps from standard simplices, capturing topological features through chains and cycles. Absolute homology specifically refers to the homology groups of a single topological space without reference to any subspace, contrasting with relative homology where pairs of spaces are studied. Both concepts underlie the broader framework of homology theories, facilitating the algebraic classification of spaces by quantifying holes of various dimensions.
Defining Singular Homology
Singular homology is a fundamental tool in algebraic topology that associates a sequence of abelian groups or modules to a topological space, capturing its shape and structure through continuous maps called singular simplices. It is defined using chains of singular simplices, boundary operators, and the resulting homology groups measure holes of different dimensions within the space. Absolute homology, often contrasted with relative homology, refers to the homology groups of a space without restricting to subspace pairs, making singular homology a primary method for defining these absolute invariants.
Understanding Absolute Homology
Absolute homology refers to the homology groups of a single topological space, capturing the intrinsic topological features without reference to any subspace, unlike singular homology which can be defined relative to pairs of spaces. Understanding absolute homology involves studying chains, cycles, and boundaries formed by singular simplices mapping into the space, revealing essential information such as Betti numbers and torsion coefficients. These homology groups provide algebraic invariants that classify spaces up to homotopy equivalence and detect holes of different dimensions within the space.
Key Differences Between Singular and Absolute Homology
Singular homology computes homology groups based on continuous maps from standard simplices into a topological space, providing a flexible and widely applicable framework for algebraic topology. Absolute homology, often synonymous with ordinary homology, refers to homology groups of a single topological space without reference to subspaces, highlighting intrinsic topological features. The key difference lies in singular homology's reliance on singular simplices and chain complexes for general topological spaces, whereas absolute homology emphasizes homology relative to the entire space itself.
Mathematical Foundations and Formalism
Singular homology constructs homology groups by applying chain complexes to all continuous maps from standard simplices into a topological space, enabling analysis of arbitrary spaces without restriction to triangulability. Absolute homology refers to the homology groups computed directly on a topological space, often as the zeroth step before introducing relative homology, corresponding to the homology of the space itself rather than a pair. The formalism relies on defining boundary operators on singular chains, with singular homology providing a universal and functorial tool compatible with homotopy theory, while absolute homology represents the inherent topological invariants expressed as homology groups of the space alone.
Applications in Algebraic Topology
Singular homology provides a flexible framework for computing topological invariants of arbitrary spaces by using continuous maps from standard simplices, making it essential in classifying spaces up to homotopy equivalence. Absolute homology, a special case of singular homology where the homology groups are defined for the entire space without reference to a subspace, simplifies analysis in situations where localized information is unnecessary or unavailable. Applications in algebraic topology include the computation of Betti numbers, detecting holes of various dimensions, and verifying topological invariants crucial for problems in manifolds, complex spaces, and fiber bundles.
Computational Aspects and Algorithms
Singular homology utilizes simplicial approximations and chain complexes to compute topological features by analyzing continuous maps from standard simplices, making it suitable for algorithmic implementation in software such as computational topology libraries. Absolute homology, dealing with homology groups of spaces relative to an empty subspace, simplifies computations by focusing solely on the entire space's chain complex without relative constraints, leading to more straightforward algorithmic procedures. Algorithms for singular homology often involve constructing boundary matrices and reducing them to compute homology groups efficiently, while absolute homology benefits from these techniques but omits additional steps needed for relative homology computations.
Examples: Comparing Results on Various Spaces
Singular homology and absolute homology often yield identical results on simple spaces like spheres and tori, both producing homology groups that reflect the number of holes in each dimension. For example, the singular homology groups of the 2-dimensional sphere S2 are H0(S2) Z, H1(S2) = 0, and H2(S2) Z, matching the absolute homology results derived from cellular complexes. Differences arise in more complex spaces such as CW-complexes with local coefficient systems, where singular homology can capture finer topological information compared to absolute homology computed via chain complexes.
Advantages and Limitations of Each Theory
Singular homology offers broad applicability to all topological spaces by using singular simplices, making it highly flexible for complex spaces but often computationally intensive due to its abstract nature. Absolute homology focuses on a specific space without reference to subspaces, providing straightforward calculations and clear geometric interpretations, though it lacks the relative information that singular homology captures. The choice between singular and absolute homology depends on the need for computational efficiency versus detailed relational data within topological structures.
Summary and Future Directions
Singular homology provides a comprehensive framework for analyzing topological spaces through continuous maps from standard simplices, capturing detailed geometric information, while absolute homology, as a special case, measures intrinsic topological features without reference to subspaces. Current research focuses on enhancing computational methods for singular homology and extending its applications in data science, particularly persistent homology for shape recognition and high-dimensional data analysis. Future directions include developing efficient algorithms for large-scale datasets and exploring generalized homology theories to bridge gaps between algebraic topology and applied fields.
Singular homology Infographic
 libterm.com
libterm.com