Fiber plays a crucial role in maintaining digestive health by promoting regular bowel movements and preventing constipation. Soluble fiber helps regulate blood sugar levels and lower cholesterol, while insoluble fiber supports gut health and enhances satiety. Discover how incorporating fiber-rich foods into your diet can improve your overall well-being by reading the rest of this article.
Table of Comparison
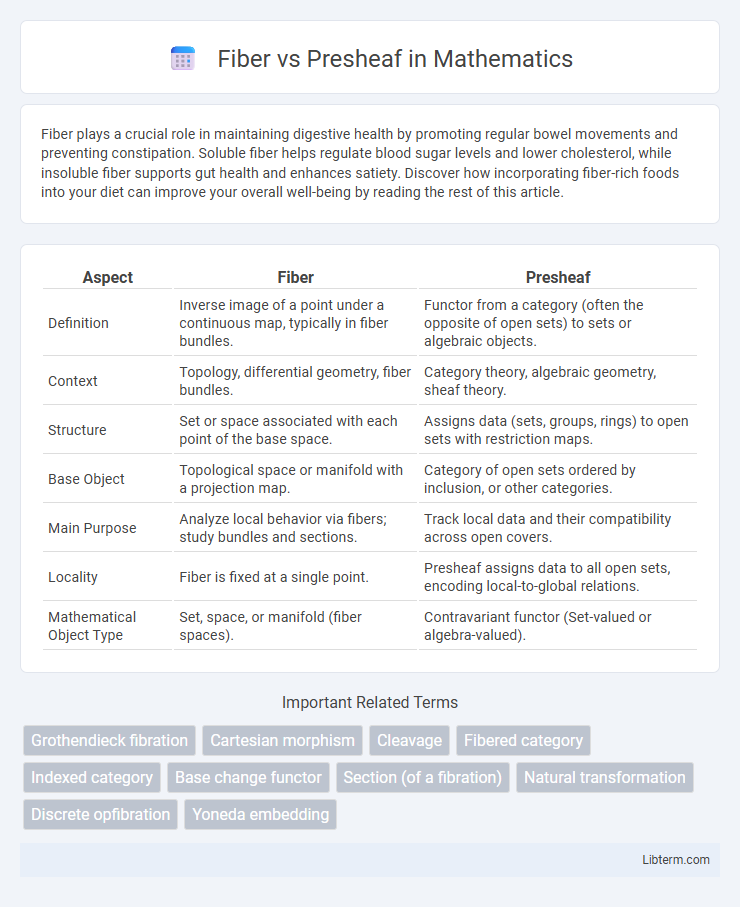
| Aspect | Fiber | Presheaf |
|---|---|---|
| Definition | Inverse image of a point under a continuous map, typically in fiber bundles. | Functor from a category (often the opposite of open sets) to sets or algebraic objects. |
| Context | Topology, differential geometry, fiber bundles. | Category theory, algebraic geometry, sheaf theory. |
| Structure | Set or space associated with each point of the base space. | Assigns data (sets, groups, rings) to open sets with restriction maps. |
| Base Object | Topological space or manifold with a projection map. | Category of open sets ordered by inclusion, or other categories. |
| Main Purpose | Analyze local behavior via fibers; study bundles and sections. | Track local data and their compatibility across open covers. |
| Locality | Fiber is fixed at a single point. | Presheaf assigns data to all open sets, encoding local-to-global relations. |
| Mathematical Object Type | Set, space, or manifold (fiber spaces). | Contravariant functor (Set-valued or algebra-valued). |
Introduction to Fiber and Presheaf
A fiber in mathematics refers to the preimage of a point under a given map, crucial in the study of fiber bundles where each fiber locally resembles a standard space. A presheaf assigns data to open sets of a topological space, governed by restriction maps that respect set inclusion, thereby organizing local information coherently. Understanding fibers provides insight into geometric structures, while presheaves serve as foundational tools in sheaf theory and algebraic geometry to handle varying local data.
Mathematical Foundations of Fiber
The mathematical foundations of fiber lie in the realm of fiber bundles, which are topological spaces locally resembling a product space but globally may exhibit complex twisting. Fibers serve as the inverse images of points under continuous surjective maps and are fundamental in defining sections, which correspond to assignments of elements in each fiber parametrized by base space points. In contrast, presheaves systematically assign algebraic or geometric structures to open sets, capturing local data without the necessity of gluing conditions that define sheaves, making fibers a more geometric concept while presheaves abstract local-to-global data behavior in topology and category theory.
Understanding Presheaf Structures
Understanding presheaf structures involves grasping the assignment of data or algebraic structures to open sets in a topological space along with restriction maps that relate these data on overlapping sets. Unlike fibers, which capture local data at a single point, presheaves organize data over varying open subsets, allowing for coherent and flexible tracking of local-to-global information. This framework forms the foundation for sheaf theory, enabling advanced applications in algebraic geometry and topology by systematically managing local sections and their compatibility.
Key Differences Between Fiber and Presheaf
Fiber refers to the inverse image of a point under a continuous map, representing local data associated with each element in the base space, while a presheaf assigns algebraic structures or sets to open subsets of a topological space with restriction maps that need not satisfy gluing conditions. The key difference is that fibers capture pointwise information, often topological or geometric, whereas presheaves organize variable local data systematically over open sets, providing a framework for sheaf theory and cohomology. Unlike fibers, presheaves emphasize consistency and locality in data assignment, enabling the reconstruction of global information from local sections.
Fiber Bundles in Topology
Fiber bundles in topology describe a space that locally resembles a product space, with fibers appearing consistently over each point of a base space, enabling structured analysis of continuous mappings. Presheaves assign algebraic or categorical data to open sets of a topological space, tracking local sections and their restrictions, forming a precursor to sheaves by capturing local-to-global properties. While fibers represent geometric slices in fiber bundles, presheaves abstract data distributions over space, bridging topology and category theory through local-global relationships.
Presheaf Theory in Category Theory
Presheaf theory in category theory involves functors from a base category to the category of sets, assigning data to each object while preserving morphisms contravariantly. Unlike fiber bundles, which focus on local trivializations over a topological space, presheaves provide a flexible framework for encoding local-to-global data without requiring gluing conditions. This approach enables abstract modeling of sheaves, cohomology, and descent theory by capturing localized information across categories.
Applications of Fiber in Modern Mathematics
Fiber concepts play a crucial role in modern mathematics, especially in differential geometry, topology, and algebraic geometry, by enabling the study of structures locally resembling product spaces, such as fiber bundles and fibrations. Applications include the classification of manifolds via fiber bundles, analysis of vector bundles in gauge theory, and the formulation of sheaf cohomology through the correspondence between fibers and stalks. These applications facilitate a deep understanding of geometric structures, homotopy theory, and moduli spaces, highlighting the foundational importance of fibers beyond the abstract setting of presheaves.
Uses of Presheaf in Algebraic Geometry
Presheaves serve as foundational tools in algebraic geometry to systematically organize local data over topological spaces, facilitating the study of sheaves and their cohomological properties. Unlike fibers, which capture pointwise information of a map, presheaves assign algebraic structures such as rings or modules to open subsets, enabling the construction of structure sheaves that define schemes and complex varieties. Their role is pivotal in defining Grothendieck topologies and handling local-to-global principles essential for modern algebraic geometry frameworks.
Comparing Categorical Perspectives
Fibers and presheaves provide distinct categorical frameworks for analyzing mathematical structures: fibers emphasize the decomposition of objects over base categories through fibered categories or Grothendieck fibrations, capturing local data varying over a domain. Presheaves offer a functorial perspective by assigning sets or objects to each element of a category, encoding global information and morphisms as contravariant functors from a category to Set or related categories. Comparing these viewpoints highlights fibers as tools for local-to-global constructions and presheaves as foundational in sheaf theory and topos theory, revealing complementary categorical insights into spatial and algebraic contexts.
Summary and Future Directions
Fibers and presheaves play crucial roles in category theory, with fibers capturing local data at points and presheaves organizing this data across varying contexts through contravariant functors. Current research explores deeper connections between fibers and sheafification processes, enhancing the understanding of local-global phenomena in algebraic geometry and topology. Future directions aim at refining computational methods for presheaves and expanding fiber-based frameworks in homotopy theory and higher category theory to address complex structural interactions.
Fiber Infographic
 libterm.com
libterm.com