Deterministic systems produce predictable outcomes based on initial conditions, ensuring consistent results every time an experiment or calculation is performed. Understanding deterministic processes is crucial for applications in fields like computer science, physics, and engineering, where precise control and repeatability are essential. Explore the rest of this article to uncover how determinism influences technology and decision-making in your daily life.
Table of Comparison
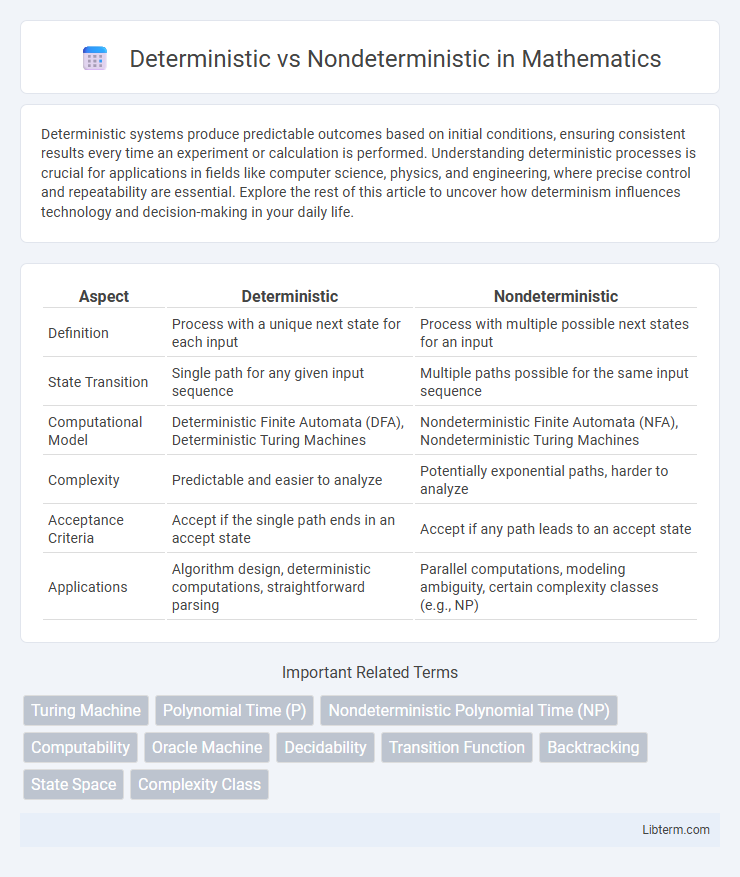
| Aspect | Deterministic | Nondeterministic |
|---|---|---|
| Definition | Process with a unique next state for each input | Process with multiple possible next states for an input |
| State Transition | Single path for any given input sequence | Multiple paths possible for the same input sequence |
| Computational Model | Deterministic Finite Automata (DFA), Deterministic Turing Machines | Nondeterministic Finite Automata (NFA), Nondeterministic Turing Machines |
| Complexity | Predictable and easier to analyze | Potentially exponential paths, harder to analyze |
| Acceptance Criteria | Accept if the single path ends in an accept state | Accept if any path leads to an accept state |
| Applications | Algorithm design, deterministic computations, straightforward parsing | Parallel computations, modeling ambiguity, certain complexity classes (e.g., NP) |
Introduction to Deterministic and Nondeterministic Concepts
Deterministic systems operate with a fixed set of rules, producing a unique outcome for each specific input, ensuring predictability and consistency. Nondeterministic systems allow multiple possible outcomes from the same input due to inherent randomness or concurrency, which models complex scenarios where uncertainty or parallel processes exist. Understanding these concepts is fundamental in computer science, particularly in automata theory, algorithm design, and complexity analysis.
Defining Deterministic Systems
Deterministic systems operate under strict rules where the current state and inputs uniquely determine the next state, ensuring predictable and repeatable outcomes. These systems are characterized by a lack of randomness, meaning that the same initial conditions always lead to the same results, as seen in classical physics and deterministic algorithms. Defining deterministic systems involves specifying state-transition functions that map each state and input pair to exactly one subsequent state, enabling precise modeling and analysis.
Understanding Nondeterministic Systems
Nondeterministic systems exhibit multiple possible future states from a single current state, unlike deterministic systems where the next state is precisely determined by current conditions. In computation theory, nondeterministic models, such as nondeterministic finite automata (NFA), allow simultaneous exploration of multiple paths, enabling more flexible problem-solving and parallel state transitions. Understanding nondeterministic systems is crucial for analyzing algorithms, complexity classes like NP, and modeling real-world processes with inherent uncertainty or concurrency.
Key Differences between Deterministic and Nondeterministic
Deterministic models produce a single, predictable outcome for a given input, ensuring consistency and repeatability in computation or process execution. Nondeterministic models allow multiple possible outcomes from the same input, representing scenarios that involve uncertainty or parallel possibilities. Key differences include predictability, with deterministic systems having a unique state transition, while nondeterministic systems can transition to multiple states, impacting complexity and problem-solving approaches in computer science and automata theory.
Real-World Examples of Deterministic Processes
Deterministic processes follow a set of predefined rules, producing the same output from identical initial conditions, exemplified by classical physics phenomena like planetary motion and electrical circuits where outcomes are predictable and reproducible. In computer science, sorting algorithms such as Merge Sort and Bubble Sort represent deterministic processes, consistently yielding the same sorted list when provided with the same input. Manufacturing assembly lines also demonstrate deterministic behavior through standardized procedures ensuring consistent product quality and output.
Real-World Examples of Nondeterministic Processes
Nondeterministic processes frequently appear in real-world scenarios such as stock market fluctuations, weather forecasting, and human decision-making, where outcomes cannot be precisely predicted due to inherent randomness or incomplete information. These processes contrast with deterministic systems like classical mechanics or algorithmic computations, which yield consistent results under identical conditions. Understanding nondeterministic behavior is critical in fields like machine learning, robotics, and finance, where models must accommodate uncertainty and probabilistic outcomes.
Deterministic vs Nondeterministic in Computer Science
Deterministic models in computer science follow a fixed sequence of operations where each input state leads to exactly one subsequent state, enabling predictable and reproducible outcomes. Nondeterministic models, such as nondeterministic finite automata (NFA), allow multiple possible next states from a given input, representing concurrent or parallel computations that can be explored simultaneously. The distinction is critical in complexity theory, where deterministic algorithms run in polynomial time (P), while nondeterministic algorithms define the class NP, central to understanding computational problem-solving limits.
The Role of Randomness and Uncertainty
Deterministic systems operate under predictable rules where outputs consistently follow from specific inputs, eliminating randomness and uncertainty. Nondeterministic systems incorporate elements of randomness or incomplete information, causing multiple possible outcomes from the same initial conditions. This inherent uncertainty plays a crucial role in fields such as quantum computing, cryptography, and probabilistic algorithms, where unpredictability influences computation and decision-making.
Advantages and Limitations of Each Approach
Deterministic algorithms offer predictability and reproducibility, enabling consistent outputs for identical inputs, which is crucial in real-time systems and safety-critical applications. Nondeterministic approaches provide flexibility and potential efficiency gains by exploring multiple computational paths simultaneously, beneficial in solving complex problems like optimization and search tasks. However, deterministic methods can be limited by their inability to adapt to varying conditions, while nondeterministic algorithms may face challenges with unpredictability and increased computational overhead.
Practical Applications and Future Trends
Deterministic algorithms, widely used in fields such as cryptography, network routing, and real-time systems, guarantee predictable and reproducible outcomes, ensuring reliability in mission-critical applications. Nondeterministic approaches, including quantum computing and heuristic optimization, are pivotal in solving complex problems like machine learning model training and combinatorial optimization where multiple potential solutions exist. Future trends indicate a convergence where hybrid models leverage deterministic precision alongside nondeterministic flexibility to enhance efficiency in artificial intelligence, cybersecurity, and large-scale data analytics.
Deterministic Infographic
 libterm.com
libterm.com