Fredholm operators are bounded linear operators between Banach spaces with finite-dimensional kernel and cokernel, and a closed range. They play a crucial role in functional analysis, particularly in solving integral equations and studying index theory. Explore the rest of this article to understand how Fredholm operators impact your mathematical insights and applications.
Table of Comparison
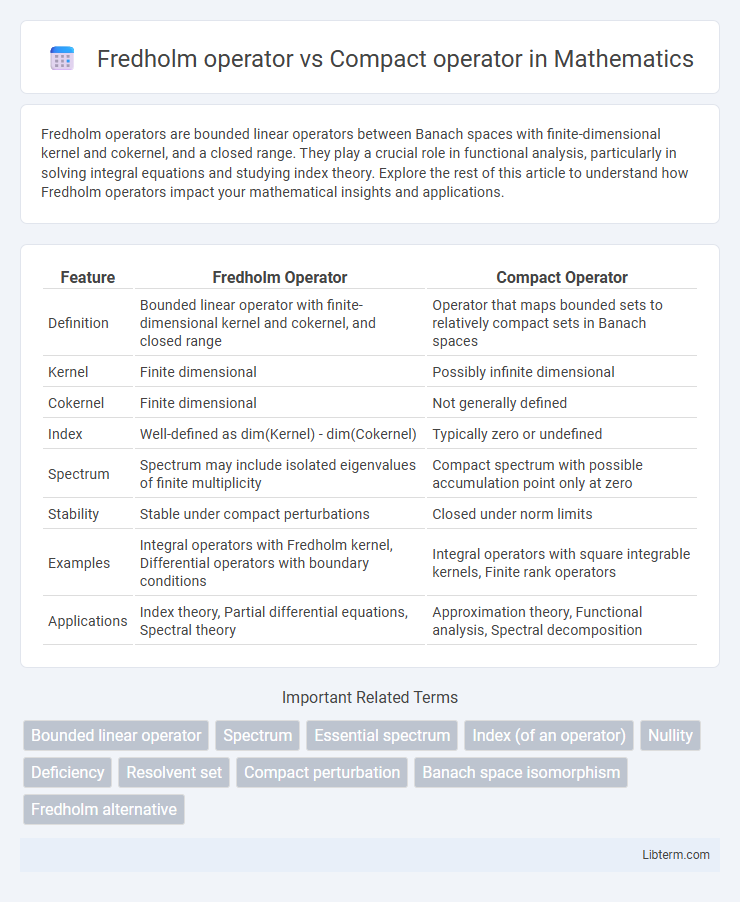
| Feature | Fredholm Operator | Compact Operator |
|---|---|---|
| Definition | Bounded linear operator with finite-dimensional kernel and cokernel, and closed range | Operator that maps bounded sets to relatively compact sets in Banach spaces |
| Kernel | Finite dimensional | Possibly infinite dimensional |
| Cokernel | Finite dimensional | Not generally defined |
| Index | Well-defined as dim(Kernel) - dim(Cokernel) | Typically zero or undefined |
| Spectrum | Spectrum may include isolated eigenvalues of finite multiplicity | Compact spectrum with possible accumulation point only at zero |
| Stability | Stable under compact perturbations | Closed under norm limits |
| Examples | Integral operators with Fredholm kernel, Differential operators with boundary conditions | Integral operators with square integrable kernels, Finite rank operators |
| Applications | Index theory, Partial differential equations, Spectral theory | Approximation theory, Functional analysis, Spectral decomposition |
Introduction to Fredholm and Compact Operators
Fredholm operators are bounded linear operators between Banach spaces with finite-dimensional kernel and cokernel, and a closed range, playing a crucial role in functional analysis and index theory. Compact operators map bounded sets to relatively compact sets, exhibiting properties similar to finite-rank operators and serving as key tools in spectral theory. Understanding the distinctions helps analyze operator spectra, stability of solutions, and perturbation effects in infinite-dimensional spaces.
Defining Fredholm Operators
Fredholm operators are bounded linear operators between Banach spaces characterized by having a finite-dimensional kernel, a closed range, and a finite-dimensional cokernel. In contrast, compact operators map bounded sets to relatively compact sets, often lacking these dimensional restrictions. The index of a Fredholm operator, defined as the difference between the dimension of its kernel and cokernel, is a key invariant not shared by general compact operators.
Understanding Compact Operators
Compact operators are linear operators on Banach or Hilbert spaces that map bounded sets to relatively compact sets, ensuring every sequence has a convergent subsequence. They play a crucial role in functional analysis as they generalize the notion of matrices with finite rank and facilitate spectral theory by having discrete spectra accumulating only at zero. Understanding compact operators provides insight into Fredholm operators, which are perturbations of the identity by compact operators, characterized by having finite-dimensional kernels and cokernels with closed range.
Essential Differences Between Fredholm and Compact Operators
Fredholm operators are characterized by having a finite-dimensional kernel and cokernel, and an index defined as the difference between these dimensions, while compact operators generally have infinite-dimensional null spaces and lack a well-defined index. Essential spectrum remains stable under compact perturbations, making Fredholm operators crucial for studying spectral properties in functional analysis. Unlike compact operators that map bounded sets into relatively compact sets, Fredholm operators maintain invertibility modulo compact operators, highlighting their fundamental differences in operator theory.
Spectrum Analysis: Fredholm vs Compact
Fredholm operators exhibit a spectrum consisting of isolated eigenvalues with finite multiplicity and a possible continuous spectrum linked to the essential spectrum, while compact operators have a spectrum containing zero and a sequence of eigenvalues accumulating only at zero. The essential spectrum of a Fredholm operator remains stable under compact perturbations, highlighting differences in spectral stability compared to purely compact operators. Understanding these spectral distinctions is crucial in operator theory, impacting the solvability of integral equations and stability analysis in functional analysis.
Index Theory and Fredholm Operators
Fredholm operators are bounded linear operators on Banach spaces characterized by having a finite-dimensional kernel and cokernel, with a closed range, making their index--the difference between the dimension of the kernel and cokernel--a central invariant in index theory. In contrast, compact operators, while often perturbations that preserve Fredholm properties, typically have essential spectrum reduced to zero, enabling crucial stability results in Fredholm theory. The Atiyah-Singer Index Theorem fundamentally connects the analytical index of Fredholm operators with topological invariants, emphasizing their pivotal role in geometric analysis and partial differential equations.
Role of Compact Operators in Functional Analysis
Compact operators play a crucial role in functional analysis by enabling the approximation of Fredholm operators, which are integral in solving linear equations on infinite-dimensional spaces. They exhibit properties similar to finite-dimensional operators, such as having a discrete spectrum with possible accumulation only at zero, facilitating spectral theory development. Fredholm operators often arise as perturbations of invertible operators by compact operators, making compact operators essential in index theory and stability analysis.
Applications in Partial Differential Equations
Fredholm operators play a crucial role in solving boundary value problems for partial differential equations (PDEs) by ensuring the existence and uniqueness of solutions through index theory and the Fredholm alternative. Compact operators, often arising as integral operators with smooth kernels, are used to approximate more complex operators in PDE analysis, enabling spectral theory applications and perturbation methods. The interplay between Fredholm and compact operators facilitates the treatment of elliptic PDEs, where Fredholm operators enable decomposition of solution spaces, and compact operators assist in establishing the compactness required for various existence theorems.
Examples Illustrating Fredholm and Compact Operators
Fredholm operators include integral operators with kernels having finite-dimensional null spaces and cokernels, such as the identity plus a compact perturbation on a Hilbert space. Compact operators frequently appear as integral operators with square-integrable kernels or as limits of finite-rank operators, exemplified by the Volterra operator on L2[0,1]. The difference between Fredholm and compact operators is illustrated by Fredholm operators having index and invertibility modulo compacts, while compact operators always have spectrum accumulating at zero only.
Conclusion: Choosing the Right Operator
Fredholm operators are integral for solving linear equations due to their index properties and stability under perturbations, making them ideal for applications requiring robust invertibility conditions. Compact operators, characterized by their approximation of identity and spectral properties, excel in scenarios demanding compactness and manageable eigenvalue spectra. Selecting between Fredholm and compact operators hinges on the problem's demands for index stability or spectral compactness, ensuring optimal analytical and numerical performance.
Fredholm operator Infographic
 libterm.com
libterm.com