Dual technology combines two different systems to enhance performance and efficiency in various applications, from electronics to linguistics. Understanding how dual systems work can provide unique insights and practical advantages for your projects or daily tasks. Discover more about the benefits and uses of dual technology in the full article.
Table of Comparison
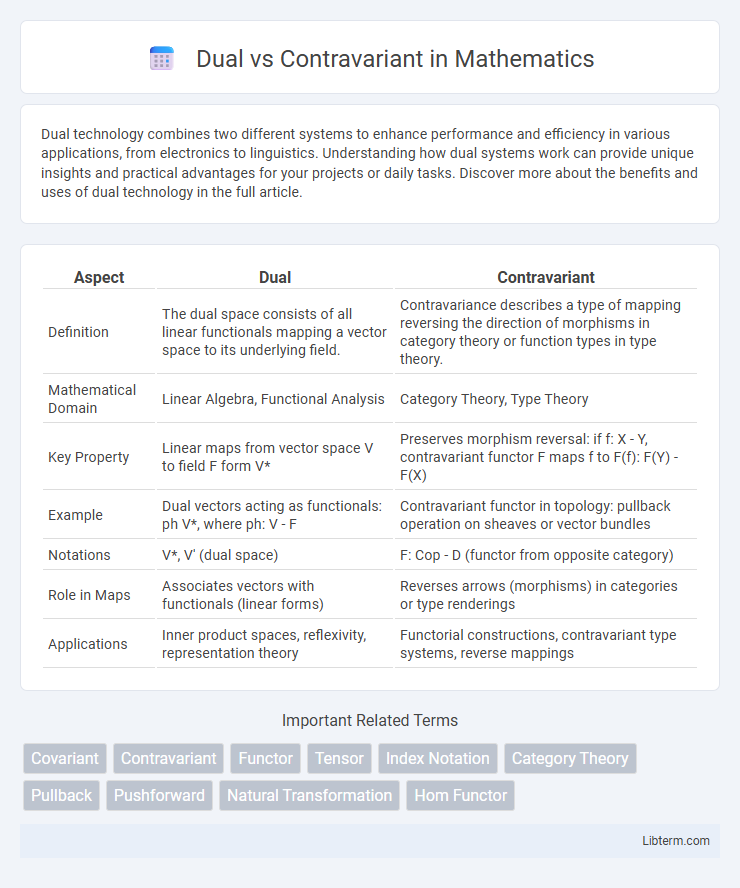
| Aspect | Dual | Contravariant |
|---|---|---|
| Definition | The dual space consists of all linear functionals mapping a vector space to its underlying field. | Contravariance describes a type of mapping reversing the direction of morphisms in category theory or function types in type theory. |
| Mathematical Domain | Linear Algebra, Functional Analysis | Category Theory, Type Theory |
| Key Property | Linear maps from vector space V to field F form V* | Preserves morphism reversal: if f: X - Y, contravariant functor F maps f to F(f): F(Y) - F(X) |
| Example | Dual vectors acting as functionals: ph V*, where ph: V - F | Contravariant functor in topology: pullback operation on sheaves or vector bundles |
| Notations | V*, V' (dual space) | F: Cop - D (functor from opposite category) |
| Role in Maps | Associates vectors with functionals (linear forms) | Reverses arrows (morphisms) in categories or type renderings |
| Applications | Inner product spaces, reflexivity, representation theory | Functorial constructions, contravariant type systems, reverse mappings |
Introduction to Dual and Contravariant Concepts
Dual and contravariant concepts arise primarily in category theory and type theory, characterizing opposite or reversed structures. The dual of a category reverses the direction of all morphisms, transforming objects and arrows into their counterparts, while contravariance in type systems refers to function parameter types that vary oppositely to their original direction. Understanding these notions is crucial for grasping advanced topics such as adjoint functors, function subtyping, and covariance-contravariance relationships in programming language design.
Understanding Duality in Mathematics and Programming
Duality in mathematics refers to a principle where concepts, theorems, or structures can be transformed into dual counterparts by reversing relationships, commonly seen in linear algebra with vector spaces and their dual spaces. Contravariance, in programming and category theory, specifically describes how functions or type transformations reverse the direction of morphisms, such as function argument types varying inversely to subtype relationships. Understanding duality involves recognizing how dual objects or operations correspond systematically, while contravariance highlights type safety and substitution principles in typed programming languages.
Defining Contravariance: A Semantic Perspective
Contravariance in type theory refers to the ability of a function or method to accept arguments of more general types than originally specified, effectively reversing the direction of type substitution compared to covariance. From a semantic perspective, contravariance ensures that a function expecting a specific type can safely operate with broader input types, preserving type safety in polymorphic hierarchies. This is critical in defining dual relationships in category theory, where contravariant functors reverse morphism directions, contrasting with covariant functors that preserve them.
Key Differences Between Dual and Contravariant
Dual refers to a concept in category theory where every object has a corresponding dual object, reversing morphisms' direction, while contravariant pertains to functors that reverse the direction of morphisms between categories. Key differences include duality focusing on object-level correspondence with reversed arrows, whereas contravariant functors explicitly reverse morphism direction in mappings between categories. Duality often involves an involution property, meaning the dual of a dual returns the original, contrasting with contravariant functors that may not have this involutive nature.
Real-World Examples of Duality
Duality in linear algebra manifests in real-world examples such as signal processing, where the Fourier transform pairs a time-domain signal with its frequency-domain dual, enabling efficient analysis and reconstruction. Contravariant vectors arise naturally in physics when describing changes under coordinate transformations, like velocity components that transform oppositely to the coordinate basis. These dual and contravariant concepts underpin diverse applications, including computer graphics and electromagnetic theory, by providing complementary frameworks for problem-solving.
Applications of Contravariant Functions
Contravariant functions are essential in type theory and functional programming for enabling flexible and safe type transformations, especially when dealing with input types in function parameters. They are widely applied in category theory to model duality concepts and in designing type systems that support safer subtype polymorphism through contravariant position usage. Functional languages like Scala and Haskell leverage contravariant functors to invert the direction of type mappings, facilitating advanced data manipulation and abstraction patterns.
Dual vs Contravariant: Use Cases in Type Systems
Dual type systems enable transforming covariant types into contravariant types, enhancing flexibility in function argument handling and interface design. Contravariant types excel in scenarios where input types need restriction, such as event handlers or consumer interfaces, ensuring type-safe function parameter substitution. Using duality principles allows type systems to leverage both covariant and contravariant properties, improving expressiveness and robustness in complex type hierarchies.
Advantages and Limitations of Duality
Duality in category theory provides a powerful framework to transform problems by reversing morphisms, enabling the analysis of contravariant functors which map objects and arrows in opposite directions. Advantages of duality include simplifying proofs by translating concepts into their dual forms, revealing symmetries and deep structural insights across mathematical domains. Limitations arise when dualizing fails to preserve constructions such as limits and colimits exactly, potentially leading to loss of intuitive interpretations or computational convenience in certain contexts.
Contravariant Patterns in Functional Programming
Contravariant patterns in functional programming describe type transformations where functions handle inputs oppositely to covariance, enhancing flexibility in type composition. These patterns are crucial in scenarios such as designing type-safe event handlers, where input types can be generalized without compromising correctness. Mastery of contravariance offers improved function interoperability and robust abstraction capabilities in typed functional languages like Haskell and Scala.
Summary: Choosing Between Dual and Contravariant Approaches
Selecting between dual and contravariant approaches primarily depends on the desired direction of type transformation in programming. Dual approaches emphasize mapping types in a straightforward manner, while contravariant approaches invert the direction of type relationships, enhancing flexibility in function parameter types. Understanding the specific use case and variance requirements is essential for optimizing type safety and code reusability.
Dual Infographic
 libterm.com
libterm.com