A distributional solution leverages probability distributions to model complex systems or data patterns, providing a more flexible and robust approach than deterministic methods. This approach is essential in fields like machine learning, economics, and physics, where uncertainty and variability are inherent. Explore the rest of this article to understand how a distributional solution can transform your problem-solving strategy.
Table of Comparison
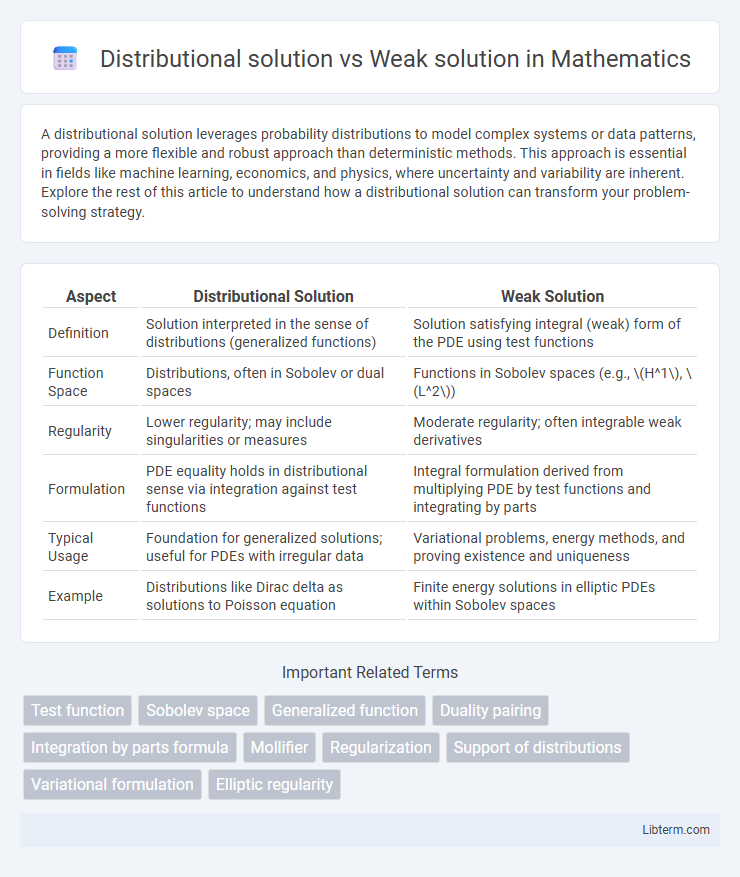
| Aspect | Distributional Solution | Weak Solution |
|---|---|---|
| Definition | Solution interpreted in the sense of distributions (generalized functions) | Solution satisfying integral (weak) form of the PDE using test functions |
| Function Space | Distributions, often in Sobolev or dual spaces | Functions in Sobolev spaces (e.g., \(H^1\), \(L^2\)) |
| Regularity | Lower regularity; may include singularities or measures | Moderate regularity; often integrable weak derivatives |
| Formulation | PDE equality holds in distributional sense via integration against test functions | Integral formulation derived from multiplying PDE by test functions and integrating by parts |
| Typical Usage | Foundation for generalized solutions; useful for PDEs with irregular data | Variational problems, energy methods, and proving existence and uniqueness |
| Example | Distributions like Dirac delta as solutions to Poisson equation | Finite energy solutions in elliptic PDEs within Sobolev spaces |
Introduction to Distributional and Weak Solutions
Distributional solutions extend classical solutions by interpreting differential equations through generalized functions, allowing for the analysis of PDEs with irregular data or singularities. Weak solutions relax differentiability requirements, using integrals and test functions to satisfy equations in an averaged sense, critical for variational problems and nonlinear PDEs. Both frameworks enable solving equations that lack classical solutions, thus broadening the scope of mathematical analysis in applied contexts.
Mathematical Foundations of Solution Concepts
Distributional solutions extend classical solutions by interpreting differential equations in the sense of distributions, allowing the inclusion of generalized functions such as Dirac delta functions. Weak solutions relax differentiability requirements by integrating against test functions, enabling the treatment of PDEs with discontinuous or less regular solutions while preserving integral formulations. Both concepts are fundamental in functional analysis and partial differential equations, providing frameworks to solve problems where classical solutions do not exist or are difficult to obtain.
Defining the Distributional Solution
The distributional solution is defined within the framework of distributions or generalized functions, extending classical solutions by allowing functions that may not be differentiable in the traditional sense. It satisfies the differential equation when integrated against a set of smooth test functions with compact support, enabling analysis of PDEs with irregular data or singularities. This approach contrasts with weak solutions by emphasizing the role of distributions in the formulation and interpretation of solutions to differential equations.
Understanding Weak Solutions
Weak solutions extend classical solutions by relaxing differentiability requirements, allowing functions with limited smoothness to satisfy partial differential equations in an integral sense. Distributional solutions generalize this concept further by interpreting derivatives as distributions, enabling the treatment of even more irregular functions within the framework of generalized functions. Understanding weak solutions is essential for solving PDEs in contexts where classical solutions do not exist, particularly in fluid dynamics and elasticity problems.
Key Differences between Distributional and Weak Solutions
Distributional solutions are defined using distributions and allow solving PDEs where classical derivatives may not exist, making them suitable for highly irregular functions. Weak solutions rely on integrating against test functions and employ Sobolev spaces, emphasizing energy methods and variational formulations over pointwise differentiation. The key difference lies in the framework: distributional solutions extend classical derivatives through generalized functions, while weak solutions focus on integral identities and function spaces accommodating less regularity.
Applications in Partial Differential Equations
Distributional solutions extend classical concepts by interpreting PDEs in the sense of distributions, enabling analysis of equations with nonsmooth data or irregular domains commonly encountered in fluid dynamics and quantum mechanics. Weak solutions relax differentiability requirements, allowing solutions in Sobolev spaces, which are crucial for proving existence and uniqueness in nonlinear PDEs like the Navier-Stokes and elliptic boundary value problems. Both frameworks facilitate the treatment of PDEs with discontinuities or singularities, providing robust methods for modern applied mathematics and numerical analysis.
Functional Spaces Involved (Distributions vs Sobolev Spaces)
Distributional solutions belong to the space of distributions (generalized functions), extending classical functions to include objects like Dirac delta, enabling the interpretation of derivatives in a weak sense. Weak solutions are typically elements of Sobolev spaces, such as \( H^1(\Omega) \), which incorporate functions with integrable derivatives, providing a functional framework for variational formulations of PDEs. These functional spaces capture different levels of regularity and integrability, with distributions allowing more singularities, while Sobolev spaces impose certain smoothness and boundary conditions for weak derivatives.
Existence and Uniqueness of Solutions
Distributional solutions offer a generalized framework for solving partial differential equations (PDEs) where classical solutions may not exist, focusing on the existence of solutions in the sense of distributions. Weak solutions extend this concept by relaxing differentiability requirements, allowing for existence and uniqueness results under broader function spaces such as Sobolev spaces. Existence and uniqueness for weak solutions often rely on variational methods and functional analysis tools, ensuring well-posedness even for PDEs with irregular data or coefficients.
Examples Illustrating Both Approaches
Distributional solutions apply generalized functions like the Dirac delta to solve differential equations where classical solutions fail, exemplified by the heat equation with initial data given by a delta distribution. Weak solutions involve integrating against test functions, allowing solutions like the shock waves in hyperbolic conservation laws, where classical derivatives do not exist. For instance, the Burgers' equation exhibits both types: the distributional approach handles singular source terms, while the weak solution framework captures discontinuous solutions consistent with physical constraints.
Conclusion and Practical Implications
Distributional solutions extend classical weak solutions by accommodating functions or distributions with lower regularity, allowing for broader applicability in partial differential equations (PDEs) with irregular data or coefficients. Weak solutions focus on integral formulations that satisfy PDEs in an averaged sense, ensuring existence and uniqueness under specific boundary and smoothness conditions. The practical implication is that distributional solutions enable modeling and analysis of more complex physical phenomena where classical or weak solutions fail, enhancing numerical methods and theoretical frameworks in engineering and physics.
Distributional solution Infographic
 libterm.com
libterm.com