The spectrum of a ring, denoted as Spec(R), is the set of all prime ideals of a ring R, equipped with the Zariski topology. This fundamental concept in algebraic geometry connects algebraic properties with geometric intuition, allowing you to study the structure of rings through their prime ideals. Explore the rest of the article to deepen your understanding of how the spectrum of a ring shapes modern mathematical theory.
Table of Comparison
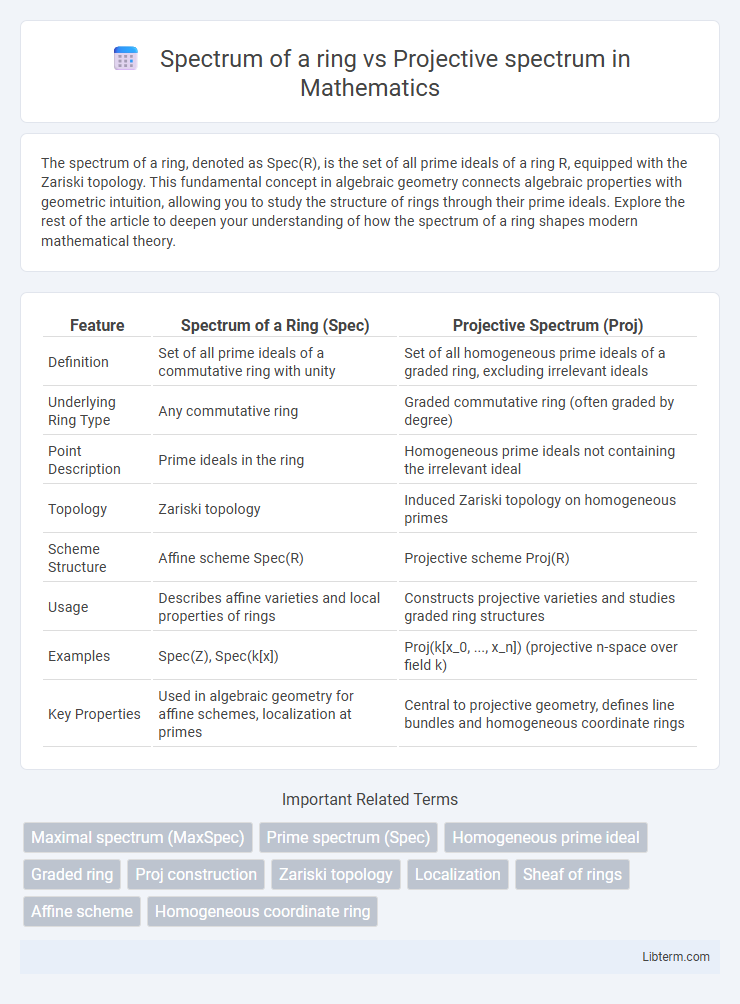
| Feature | Spectrum of a Ring (Spec) | Projective Spectrum (Proj) |
|---|---|---|
| Definition | Set of all prime ideals of a commutative ring with unity | Set of all homogeneous prime ideals of a graded ring, excluding irrelevant ideals |
| Underlying Ring Type | Any commutative ring | Graded commutative ring (often graded by degree) |
| Point Description | Prime ideals in the ring | Homogeneous prime ideals not containing the irrelevant ideal |
| Topology | Zariski topology | Induced Zariski topology on homogeneous primes |
| Scheme Structure | Affine scheme Spec(R) | Projective scheme Proj(R) |
| Usage | Describes affine varieties and local properties of rings | Constructs projective varieties and studies graded ring structures |
| Examples | Spec(Z), Spec(k[x]) | Proj(k[x_0, ..., x_n]) (projective n-space over field k) |
| Key Properties | Used in algebraic geometry for affine schemes, localization at primes | Central to projective geometry, defines line bundles and homogeneous coordinate rings |
Introduction to Spectra in Algebraic Geometry
The spectrum of a ring, denoted Spec(R), consists of all prime ideals of a commutative ring R, equipped with the Zariski topology and a structure sheaf, forming a fundamental affine scheme in algebraic geometry. The projective spectrum, or Proj(R), generalizes Spec(R) to graded rings, capturing equivalence classes of homogeneous prime ideals and providing the foundation for projective schemes. Both spectra serve as crucial tools for translating algebraic properties of rings into geometric objects, enabling the study of varieties and schemes through their structural and topological characteristics.
Defining the Spectrum of a Ring (Spec)
The spectrum of a ring, denoted as Spec(R), is the set of all prime ideals of a commutative ring R equipped with the Zariski topology, serving as a fundamental construction in algebraic geometry. Each point in Spec(R) corresponds to a prime ideal, capturing algebraic information and enabling the definition of schemes. In contrast, the projective spectrum, Proj(R), generalizes this concept to graded rings, focusing on homogeneous prime ideals and providing a framework for projective varieties.
Understanding the Projective Spectrum (Proj)
The Projective Spectrum (Proj) of a graded ring extends the concept of the Spectrum (Spec) by focusing on homogeneous prime ideals, capturing the geometric essence of projective varieties. Unlike Spec, which parametrizes all prime ideals in a ring, Proj filters these ideals to those relevant for projective geometry, enabling the construction of projective schemes with a natural grading structure. Understanding Proj requires recognizing its role in encoding the projective coordinate ring's graded structure, forming the foundation for studying projective algebraic geometry.
Construction and Topology of Spec
The spectrum of a ring, denoted Spec(R), is constructed as the set of all prime ideals of a commutative ring R, equipped with the Zariski topology where closed sets correspond to vanishing loci of ring elements. In contrast, the projective spectrum, Proj(R), arises from a graded ring and consists of homogeneous prime ideals not containing the irrelevant ideal, forming a topological space with a Zariski topology adapted to homogeneous elements. The topology on Spec(R) is defined via basic open sets D(f) for f in R, while on Proj(R), open sets D_+(f) use homogeneous elements to respect grading, reflecting differences in geometric interpretation and local structure.
Construction and Topology of Proj
The spectrum of a ring, Spec(R), consists of all prime ideals of a commutative ring R and is endowed with the Zariski topology, where closed sets correspond to vanishing sets of ideals. The projective spectrum, Proj(S), constructed from a graded ring S, parametrizes homogeneous prime ideals not containing the irrelevant ideal, inheriting a topology generated by distinguished open sets defined by homogeneous elements. Proj's structure sheaf endows it with a scheme structure reflecting localizations at homogeneous elements, capturing projective geometric properties absent in the simpler affine construction of Spec.
Affine vs. Projective Schemes
The spectrum of a ring, denoted Spec(R), forms the foundational example of an affine scheme and consists of prime ideals equipped with the Zariski topology and a structure sheaf. In contrast, the projective spectrum, Proj(S), of a graded ring S constructs projective schemes by gluing spectra of degree-zero parts of certain localizations, capturing the geometry of projective varieties. Affine schemes correspond to algebraic varieties in affine space, while projective schemes generalize this to projective space, allowing a systematic treatment of homogenized coordinate rings and line bundles.
Morphisms Involving Spec and Proj
Morphisms involving Spec and Proj capture fundamental dualities between algebraic structures and geometric objects in algebraic geometry. The functor Spec assigns to a commutative ring R its prime spectrum Spec(R), a topological space endowed with the Zariski topology, while Proj associates a graded ring to a projective scheme, encoding homogeneous prime ideals. Morphisms from Spec correspond to ring homomorphisms, reflecting contravariant behavior, whereas morphisms involving Proj correspond to graded ring homomorphisms preserving degrees, ensuring compatibility with projective geometric structures.
Examples and Key Differences
The Spectrum of a ring, denoted Spec(R), consists of all prime ideals of a commutative ring R and forms the cornerstone of affine algebraic geometry, with examples including Spec(Z) representing prime numbers as points. In contrast, the Projective Spectrum, or Proj(R), applies to graded rings and encodes homogeneous prime ideals, capturing projective varieties such as Proj(k[x,y,z]) corresponding to the projective plane over a field k. Key differences lie in their construction: Spec(R) handles arbitrary rings focusing on local properties, while Proj(R) restricts to graded rings emphasizing geometric points in projective space, with Proj requiring a grading to define open sets that mimic projective geometry's homogeneous coordinate behavior.
Applications in Algebraic Geometry
The spectrum of a ring, Spec(R), represents the set of prime ideals endowed with the Zariski topology, serving as a fundamental building block in algebraic geometry for constructing affine schemes and studying local properties of varieties. The projective spectrum, Proj(R), generalizes Spec(R) to graded rings, enabling the construction of projective schemes that model projective varieties and incorporate homogeneous coordinate rings. Applications in algebraic geometry include using Spec(R) to analyze local ring structures and singularities, while Proj(R) facilitates the study of line bundles, divisors, and embedding of varieties into projective space.
Conclusion: Comparing Spec and Proj
The spectrum of a ring, Spec(R), captures prime ideals of a commutative ring and serves as a foundational tool in affine algebraic geometry, encoding local algebraic structure and topological properties. In contrast, the projective spectrum, Proj(R), arises from graded rings and parametrizes homogeneous prime ideals, providing a framework for studying projective varieties and sheaves on projective schemes. The key distinction is that Spec(R) reflects affine schemes with their Zariski topology, while Proj(R) models projective schemes, incorporating grading to handle notions of degree and allowing construction of geometrically meaningful compactifications.
Spectrum of a ring Infographic
 libterm.com
libterm.com