Positive semidefinite matrices are fundamental in optimization, statistics, and machine learning, ensuring non-negative eigenvalues and preserving convexity in quadratic forms. Their properties guarantee stable solutions in systems involving covariance matrices and kernel methods. Explore the rest of this article to understand how positive semidefinite matrices impact your computational tasks.
Table of Comparison
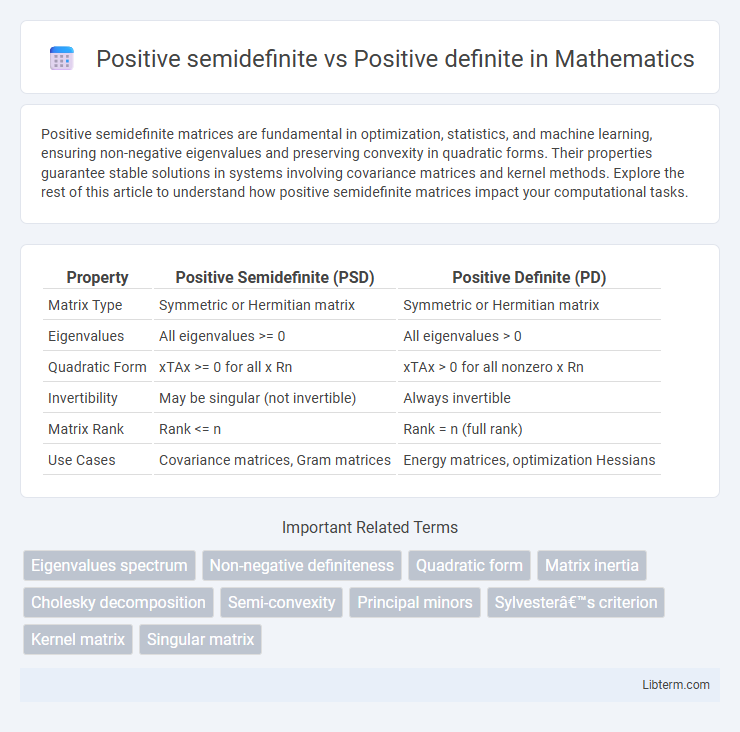
| Property | Positive Semidefinite (PSD) | Positive Definite (PD) |
|---|---|---|
| Matrix Type | Symmetric or Hermitian matrix | Symmetric or Hermitian matrix |
| Eigenvalues | All eigenvalues >= 0 | All eigenvalues > 0 |
| Quadratic Form | xTAx >= 0 for all x Rn | xTAx > 0 for all nonzero x Rn |
| Invertibility | May be singular (not invertible) | Always invertible |
| Matrix Rank | Rank <= n | Rank = n (full rank) |
| Use Cases | Covariance matrices, Gram matrices | Energy matrices, optimization Hessians |
Introduction to Matrix Definiteness
Matrix definiteness classifies matrices based on the sign of their quadratic forms, where a matrix is positive definite if all eigenvalues are strictly positive, ensuring \(x^T A x > 0\) for any nonzero vector \(x\). Positive semidefinite matrices allow eigenvalues to be zero, meaning \(x^T A x \geq 0\) for all vectors \(x\), which implies the matrix can be singular. This distinction is fundamental in optimization and numerical analysis, influencing stability and convergence properties.
Definitions: Positive Semidefinite vs Positive Definite
A positive definite matrix is a symmetric matrix where all eigenvalues are strictly greater than zero, ensuring that for any non-zero vector x, the quadratic form xTAx is positive. A positive semidefinite matrix is also symmetric, but its eigenvalues are non-negative, meaning the quadratic form xTAx is always greater than or equal to zero for any vector x. The key distinction lies in the eigenvalue spectrum: positive definite matrices have strictly positive eigenvalues, while positive semidefinite matrices allow zero eigenvalues.
Mathematical Criteria and Conditions
Positive definite matrices are symmetric matrices with all positive eigenvalues, ensuring \( x^T A x > 0 \) for every nonzero vector \( x \in \mathbb{R}^n \). Positive semidefinite matrices also require symmetry but have all nonnegative eigenvalues, satisfying \( x^T A x \geq 0 \) for all vectors \( x \), allowing for zero eigenvalues. Key mathematical criteria include the principal minors test: all leading principal minors must be strictly positive for positive definiteness, whereas they must be nonnegative for positive semidefiniteness.
Key Differences Between Positive Semidefinite and Positive Definite
Positive definite matrices have strictly positive eigenvalues, ensuring all quadratic forms xTAx are strictly greater than zero for any non-zero vector x, while positive semidefinite matrices allow eigenvalues to be zero, leading to non-negative quadratic forms that can equal zero. Positive definite matrices are always invertible, whereas positive semidefinite matrices may be singular and non-invertible. This distinction is critical in optimization problems, numerical stability, and mathematical modeling where matrix invertibility and strict positivity influence solution uniqueness and convergence.
Examples and Illustrative Matrices
Positive semidefinite matrices include examples like \( \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \) which have non-negative eigenvalues such as 3 and 1, making all quadratic forms \(x^T A x \geq 0\). Positive definite matrices exemplified by \( \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} \) have strictly positive eigenvalues ensuring \(x^T A x > 0\) for all nonzero vectors \(x\). The matrix \( \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \) is positive semidefinite but not positive definite since it has an eigenvalue zero, illustrating the key difference between the two classes.
Eigenvalues: A Fundamental Perspective
Positive definite matrices have strictly positive eigenvalues, ensuring all eigenvalues are greater than zero, which guarantees invertibility and uniqueness of solutions in systems of linear equations. Positive semidefinite matrices require all eigenvalues to be non-negative, allowing for zero eigenvalues and thus possibly leading to singular matrices that are not invertible. This fundamental distinction critically impacts stability, optimization problems, and spectral properties in linear algebra and related applications.
Applications in Machine Learning and Optimization
Positive definite matrices guarantee strictly positive eigenvalues, ensuring unique solutions in optimization problems like quadratic programming and enabling convergence in machine learning algorithms such as kernel methods and covariance estimation. Positive semidefinite matrices allow zero eigenvalues, making them essential for representing covariance matrices in Gaussian processes and defining valid kernel functions that maintain convexity but may lead to degenerate solutions. Both matrix types are critical in ensuring convexity of loss functions, stability of gradient-based optimization methods, and reliable generalization performance in supervised learning models.
Practical Implications in Linear Algebra
Positive definite matrices guarantee unique solutions in systems of linear equations and ensure stability in optimization problems, making them essential for numerical methods like Cholesky decomposition. Positive semidefinite matrices, while allowing for zero eigenvalues, are crucial in applications such as covariance matrices in statistics where non-negativity of variances is required but strict positivity is not. In machine learning, positive definite kernels enable proper feature mappings, whereas positive semidefinite kernels support similarity measures without enforcing invertibility, affecting the choice of algorithms and computational efficiency.
Testing for Positive Semidefiniteness and Positive Definiteness
Testing for positive semidefiniteness involves verifying that all eigenvalues of the matrix are non-negative, while positive definiteness requires all eigenvalues to be strictly positive. Cholesky decomposition can be used for positive definiteness, as it exists only if the matrix is positive definite; failure of decomposition indicates the matrix is not positive definite but may be positive semidefinite. Sylvester's criterion also distinguishes these properties by checking the positivity of all leading principal minors for positive definiteness, whereas non-negativity suffices for positive semidefiniteness.
Summary and Key Takeaways
Positive semidefinite matrices have non-negative eigenvalues, allowing for zero values, while positive definite matrices have strictly positive eigenvalues, implying invertibility and unique solutions in optimization problems. Positive definite matrices guarantee a strictly convex quadratic form, critical in machine learning and numerical analysis, whereas positive semidefinite matrices include boundary cases useful for stability analysis and relaxed constraints. Understanding the distinction aids in selecting appropriate mathematical models for convex optimization and system stability assessments.
Positive semidefinite Infographic
 libterm.com
libterm.com