A commutative ring spectrum is an algebraic structure in stable homotopy theory that generalizes commutative rings to the setting of spectra, incorporating both ring operations and topological data. These structures play a crucial role in modern algebraic topology, enabling computations and deeper understanding of generalized cohomology theories. Explore the rest of the article to uncover how commutative ring spectra connect abstract algebra with topological spaces and their applications.
Table of Comparison
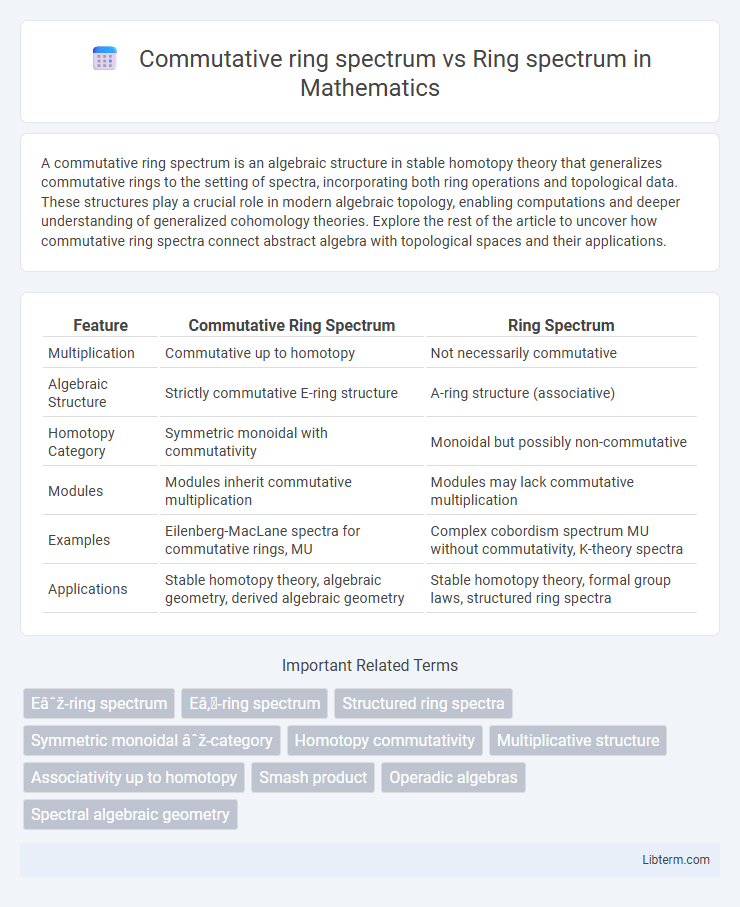
| Feature | Commutative Ring Spectrum | Ring Spectrum |
|---|---|---|
| Multiplication | Commutative up to homotopy | Not necessarily commutative |
| Algebraic Structure | Strictly commutative E-ring structure | A-ring structure (associative) |
| Homotopy Category | Symmetric monoidal with commutativity | Monoidal but possibly non-commutative |
| Modules | Modules inherit commutative multiplication | Modules may lack commutative multiplication |
| Examples | Eilenberg-MacLane spectra for commutative rings, MU | Complex cobordism spectrum MU without commutativity, K-theory spectra |
| Applications | Stable homotopy theory, algebraic geometry, derived algebraic geometry | Stable homotopy theory, formal group laws, structured ring spectra |
Introduction to Ring Spectra
In algebraic topology, a ring spectrum generalizes the notion of a ring by encoding multiplication operations at the level of spectra, providing a framework for stable homotopy theory. A commutative ring spectrum refines this structure by enforcing a homotopy-commutative multiplication, which allows for richer algebraic properties and connections to structured ring objects in stable homotopy categories. Understanding ring spectra forms the foundation for studying generalized cohomology theories and their multiplicative structures.
Defining Commutative Ring Spectra
Commutative ring spectra are structured ring spectra equipped with a multiplication map that is strictly commutative up to homotopy, aligning with the notion of E_-ring structures in stable homotopy theory. Unlike general ring spectra, which only require associative and unital multiplication possibly lacking commutativity, commutative ring spectra enforce a higher coherence that encodes commutativity at the level of all homotopies. This structure is crucial in derived algebraic geometry and stable homotopy theory, enabling the definition of generalized cohomology theories with commutative cup products and rich multiplicative properties.
Core Properties of Ring Spectra
Ring spectra are structured objects in stable homotopy theory combining ring-like multiplication with spectral properties, characterized by associativity and unit elements up to homotopy. Commutative ring spectra extend this framework by enforcing commutativity of multiplication at the level of homotopy, resulting in highly structured ring objects compatible with symmetric monoidal smash products. Key core properties of ring spectra include homotopy associative multiplication, the existence of unit maps, and module spectra structures, while commutative ring spectra additionally possess symmetric and coherent multiplication operations reflective of E-ring structures.
What Sets Commutative Ring Spectra Apart
Commutative ring spectra distinguish themselves from general ring spectra through the strict commutativity of their multiplication operation, aligning with the structure of E ring spectra in homotopy theory. This commutativity allows for richer algebraic invariants and more powerful equivalences in stable homotopy categories, facilitating structured ring operations compatible with symmetric monoidal smash products. Consequently, commutative ring spectra serve as foundational objects for advanced constructions in derived algebraic geometry and multiplicative cohomology theories.
Algebraic Structures: Noncommutative vs. Commutative
A commutative ring spectrum is an algebraic structure in stable homotopy theory where the multiplication operation is commutative up to homotopy, ensuring symmetric monoidal properties in the derived category of spectra. In contrast, a general ring spectrum may exhibit noncommutative multiplication, reflecting noncommutative algebraic structures with operations that do not necessarily commute. The distinction between commutative and noncommutative ring spectra plays a crucial role in the formulation of structured ring objects in categories of spectra, affecting homotopy-theoretic invariants and algebraic K-theory computations.
Homotopical Features in Ring Spectra
Commutative ring spectra possess a highly structured multiplication that is strictly associative and commutative up to coherent homotopies, enabling the use of powerful tools in equivariant and derived algebraic topology. Ring spectra, while associative, may lack commutativity, allowing more general homotopical constructions but complicating the algebraic manipulations related to module and algebra structures. The homotopical features of commutative ring spectra facilitate the formation of structured smash products and power operations, crucial for understanding cohomology theories and stable homotopy types.
Applications of Commutative Ring Spectra
Commutative ring spectra play a crucial role in stable homotopy theory, enabling the construction of structured ring objects in the category of spectra with commutative multiplication up to homotopy. Applications of commutative ring spectra include the development of generalized cohomology theories like topological modular forms (TMF) and the study of structured ring objects in derived algebraic geometry, providing tools for the formulation of spectral algebraic geometry. This framework facilitates advancements in equivariant homotopy theory, allowing for more refined multiplicative properties and duality phenomena than general ring spectra.
Examples in Stable Homotopy Theory
Commutative ring spectra, such as the Eilenberg-Mac Lane spectrum of a commutative ring and the sphere spectrum, provide foundational examples in stable homotopy theory with strictly commutative multiplication up to coherent homotopies. Non-commutative ring spectra arise from structured ring objects like A-ring spectra, exemplified by the Thom spectrum MU, which encodes complex cobordism but lacks strict commutativity in its multiplication. These distinctions influence the algebraic structure and operations in stable homotopy categories, affecting applications in chromatic homotopy theory and the study of power operations.
Technical Challenges and Comparisons
Commutative ring spectra impose stricter homotopical coherence conditions than general ring spectra, requiring higher-order commutativity compatible with stable homotopy operations. Constructing commutative ring spectra involves intricate obstruction theories to ensure E-ring structures, whereas ring spectra admit more flexible, often associative but not necessarily commutative, multiplicative structures. The technical challenges include managing coherence at all levels, controlling operadic actions, and ensuring compatibility with derived category frameworks, making commutative ring spectra significantly more complex in homotopical algebra contexts.
Future Directions in Ring Spectrum Research
Future directions in ring spectrum research emphasize the development of more sophisticated models for commutative ring spectra to enhance structured multiplicative properties in stable homotopy theory. Advances in higher category theory and derived algebraic geometry are expected to provide new frameworks for understanding multiplicative structures and their interactions with homotopical and algebraic invariants. Research continues to explore the applications of commutative ring spectra in equivariant stable homotopy theory and motivic homotopy theory, aiming to unify and extend classical tools in algebraic topology.
Commutative ring spectrum Infographic
 libterm.com
libterm.com