Equivalences in mathematics and logic refer to relationships where two expressions or statements hold the same value or truth under all conditions. Understanding equivalences is crucial for simplifying complex problems and ensuring accurate reasoning in your calculations. Explore the rest of this article to deepen your knowledge of equivalences and enhance your problem-solving skills.
Table of Comparison
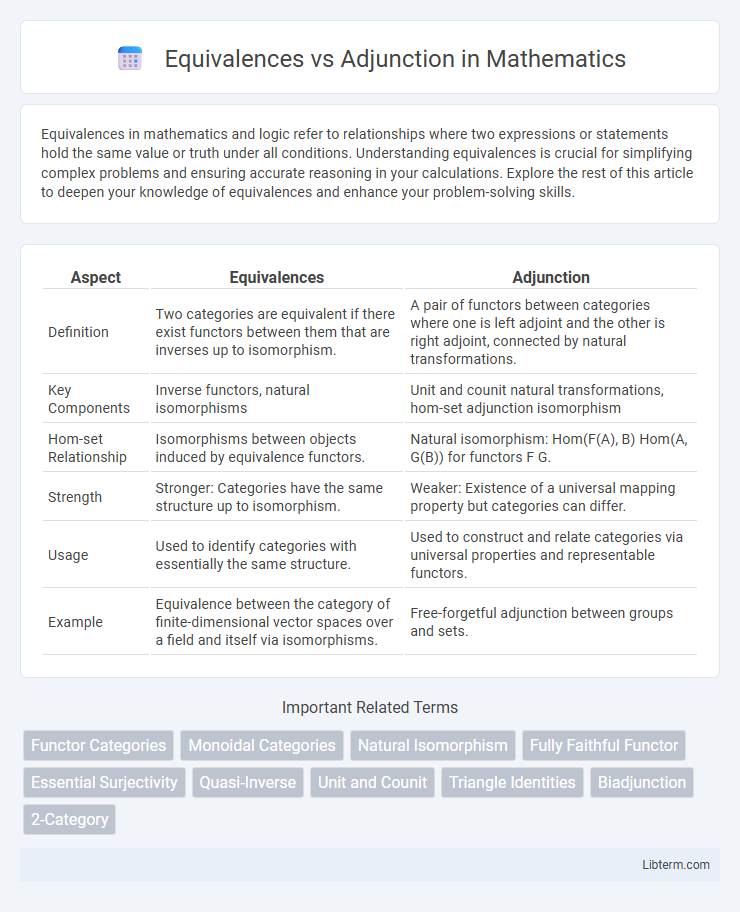
| Aspect | Equivalences | Adjunction |
|---|---|---|
| Definition | Two categories are equivalent if there exist functors between them that are inverses up to isomorphism. | A pair of functors between categories where one is left adjoint and the other is right adjoint, connected by natural transformations. |
| Key Components | Inverse functors, natural isomorphisms | Unit and counit natural transformations, hom-set adjunction isomorphism |
| Hom-set Relationship | Isomorphisms between objects induced by equivalence functors. | Natural isomorphism: Hom(F(A), B) Hom(A, G(B)) for functors F G. |
| Strength | Stronger: Categories have the same structure up to isomorphism. | Weaker: Existence of a universal mapping property but categories can differ. |
| Usage | Used to identify categories with essentially the same structure. | Used to construct and relate categories via universal properties and representable functors. |
| Example | Equivalence between the category of finite-dimensional vector spaces over a field and itself via isomorphisms. | Free-forgetful adjunction between groups and sets. |
Introduction to Equivalences and Adjunctions
Equivalences and adjunctions are foundational concepts in category theory that describe relationships between categories through functors. An equivalence occurs when two categories are connected by functors that are inverses up to natural isomorphism, ensuring they have essentially the same structure. Adjunctions generalize this idea by providing pairs of functors linked through a natural bijection between hom-sets, capturing a more flexible notion of approximation between categories.
Fundamental Definitions
Equivalences in category theory refer to a pair of functors between categories that establish an isomorphism up to natural isomorphism, ensuring that objects and morphisms correspond in a way that preserves structural properties. Adjunctions involve a pair of functors, a left adjoint and a right adjoint, connected by a natural isomorphism between hom-sets, reflecting a universal mapping property. The fundamental difference lies in equivalences requiring mutual inverses up to isomorphism, whereas adjunctions capture a more general relationship defined by a unit and counit satisfying triangle identities.
Key Properties of Equivalences
Equivalences in category theory are characterized by the existence of functors forming inverse pairs up to natural isomorphisms, ensuring full faithfulness and essential surjectivity on objects. Key properties include the preservation of limits and colimits, reflecting isomorphisms in hom-sets, and admitting quasi-inverses, which make equivalences stronger than adjunctions. Unlike adjunctions, equivalences guarantee invertibility up to isomorphism, providing a symmetrical relationship between categories.
Key Properties of Adjunctions
Adjunctions in category theory are characterized by key properties such as the existence of a pair of functors \(F : \mathcal{C} \to \mathcal{D}\) and \(G : \mathcal{D} \to \mathcal{C}\) with a natural isomorphism \(\text{Hom}_{\mathcal{D}}(F(c), d) \cong \text{Hom}_{\mathcal{C}}(c, G(d))\) for all objects \(c\) in \(\mathcal{C}\) and \(d\) in \(\mathcal{D}\). Unlike equivalences, adjunctions do not require the functors to be invertible or fully faithful but focus on establishing a universal mapping property via unit and counit natural transformations. The unit \(\eta : \text{id}_{\mathcal{C}} \to G F\) and counit \(\epsilon : F G \to \text{id}_{\mathcal{D}}\) satisfy triangular identities essential for defining adjunctions and distinguishing them from equivalences.
The Relationship Between Equivalences and Adjunctions
Equivalences in category theory arise when two categories are connected by functors forming an adjunction whose unit and counit are natural isomorphisms, ensuring both full faithfulness and essential surjectivity. The relationship between equivalences and adjunctions centers on the fact that every equivalence is an adjunction with invertible unit and counit, while not all adjunctions are equivalences due to possible non-invertibility of these natural transformations. Thus, equivalences can be seen as special cases of adjunctions where the functors establish a perfect categorical symmetry preserving structure and objects up to isomorphism.
Examples of Equivalences in Category Theory
Equivalences in category theory describe a pair of functors between categories that are inverses up to natural isomorphism, preserving categorical structure more flexibly than strict isomorphisms. A classical example of equivalence is the relationship between the category of finite-dimensional vector spaces over a field and the category of finite-dimensional free modules over that field, connected by the forgetful functor and a suitable tensor functor. Another fundamental example is the equivalence between the category of compact Hausdorff spaces and the opposite category of commutative unital C*-algebras via the Gelfand-Naimark correspondence, demonstrating how equivalences capture deep dualities in geometry and algebra.
Notable Adjunctions in Mathematical Structures
Notable adjunctions in mathematical structures include the free-forgetful adjunction, which establishes an equivalence between free objects and forgetful functors, highlighting the deep interplay between algebraic constructions and their underlying sets. Another key example is the adjunction between hom and tensor functors in category theory, which provides a foundational correspondence in enriched categories and module theory. These adjunctions underpin equivalences that characterize essential dualities in diverse areas such as algebraic topology, homological algebra, and logic, revealing the structural symmetries intrinsic to mathematical frameworks.
Criteria for Equivalences versus Adjunctions
Equivalences between categories require functors to be fully faithful and essentially surjective on objects, ensuring an isomorphism up to natural isomorphism. Adjunctions instead require a pair of functors with a unit and counit satisfying the triangle identities, but do not necessarily require the functors to be fully faithful or essentially surjective. The key criterion for equivalences is the existence of inverse functors up to isomorphism, whereas adjunctions focus on universal properties and natural transformations that mediate between hom-sets.
Applications in Mathematics and Computer Science
Equivalences and adjunctions are fundamental concepts in category theory with significant applications in both mathematics and computer science. Equivalences provide a way to identify categories that are structurally the same, enabling simplified reasoning across algebra, topology, and logic. Adjunctions give rise to important constructions such as monads and reflect core dualities, supporting semantic analysis in programming languages and the design of type systems.
Summary: Choosing Between Equivalence and Adjunction
Equivalences are strict isomorphisms between categories preserving all structural aspects, while adjunctions provide a looser, directional relationship reflecting a universal mapping property. Selecting between equivalence and adjunction depends on whether a perfect structural match is required or a more flexible, context-sensitive correspondence suffices. Applications in category theory and functional programming favor equivalences for exact structural identification and adjunctions for modeling processes like free constructions and type transformations.
Equivalences Infographic
 libterm.com
libterm.com