Maximizing a compact space requires smart storage solutions and multifunctional furniture to enhance both functionality and comfort. Utilizing vertical space and light colors can create an illusion of openness, making the area feel larger than it actually is. Discover effective tips and creative ideas to transform your compact space into a stylish and efficient haven.
Table of Comparison
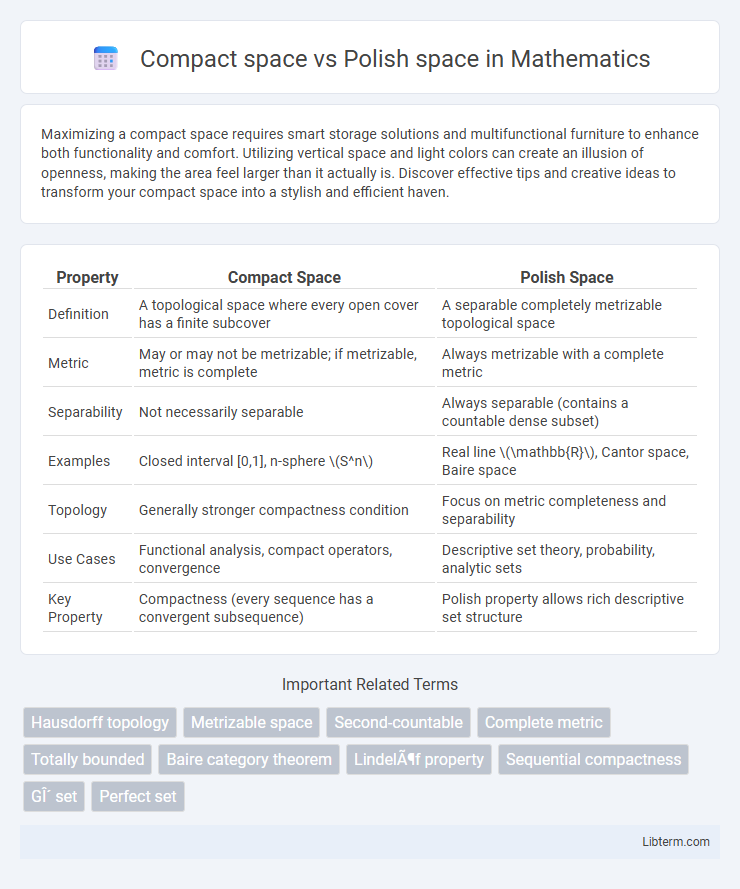
| Property | Compact Space | Polish Space |
|---|---|---|
| Definition | A topological space where every open cover has a finite subcover | A separable completely metrizable topological space |
| Metric | May or may not be metrizable; if metrizable, metric is complete | Always metrizable with a complete metric |
| Separability | Not necessarily separable | Always separable (contains a countable dense subset) |
| Examples | Closed interval [0,1], n-sphere \(S^n\) | Real line \(\mathbb{R}\), Cantor space, Baire space |
| Topology | Generally stronger compactness condition | Focus on metric completeness and separability |
| Use Cases | Functional analysis, compact operators, convergence | Descriptive set theory, probability, analytic sets |
| Key Property | Compactness (every sequence has a convergent subsequence) | Polish property allows rich descriptive set structure |
Introduction to Topological Spaces
Compact spaces are topological spaces where every open cover has a finite subcover, ensuring properties like completeness and limit point compactness. Polish spaces are separable completely metrizable spaces, meaning they admit a metric compatible with the topology that is complete and has a countable dense subset. Understanding compact and Polish spaces is fundamental in topology due to their roles in continuity, convergence, and functional analysis frameworks.
Definition of Compact Spaces
Compact spaces are topological spaces in which every open cover has a finite subcover, ensuring that the space is both limit point compact and sequentially compact in metric spaces. Polish spaces are separable completely metrizable topological spaces, often used in descriptive set theory and probability. The definition of compact spaces emphasizes finite cover properties, while Polish spaces focus on separability and complete metrizability, creating distinct classifications in general topology.
Overview of Polish Spaces
Polish spaces are complete separable metric spaces that play a central role in descriptive set theory and analysis due to their rich topological and measure-theoretic properties. Unlike compact spaces, which require every open cover to have a finite subcover, Polish spaces prioritize completeness and separability, allowing for a broader class of spaces including important examples like the real numbers with the standard metric. The study of Polish spaces involves deep connections with Borel hierarchies, continuous mappings, and probability measures, making them fundamental in modern mathematical analysis.
Key Properties of Compact Spaces
Compact spaces are topological spaces where every open cover has a finite subcover, ensuring properties like completeness and total boundedness in metric spaces. Unlike Polish spaces, which are separable and completely metrizable, compact spaces guarantee limit point compactness and sequential compactness, critical for continuity and convergence analysis. These properties make compact spaces fundamental in functional analysis and topology, controlling behavior of functions and sequences within finite constraints.
Essential Features of Polish Spaces
Polish spaces are separable and completely metrizable topological spaces, characterized by the existence of a metric that is both complete and induces a separable topology. Unlike compact spaces, which require every open cover to have a finite subcover, Polish spaces emphasize completeness and separability without necessarily being compact. This distinction makes Polish spaces fundamental in descriptive set theory and analysis due to their rich structure and ability to support measures and Borel hierarchies.
Comparison: Compactness vs Polishness
Compact spaces are characterized by every open cover having a finite subcover, ensuring limit point compactness and often simplifying continuity arguments. Polish spaces are separable completely metrizable spaces, emphasizing the existence of a compatible metric that is both complete and admits a countable dense subset. While all compact metric spaces are Polish, not all Polish spaces are compact, as Polishness prioritizes completeness and separability rather than boundedness or compactness.
Examples of Compact and Polish Spaces
The unit interval [0,1] with the standard topology is a classic example of a compact space, while the real line R with the usual metric is a foundational Polish space due to its complete separable metric structure. The Cantor set serves as both a compact and perfect Polish space, illustrating the intersection of these categories. Infinite-dimensional Hilbert spaces like l2 are Polish but not compact, highlighting the distinction between completeness, separability, and compactness.
Intersection and Differences Between Compact and Polish Spaces
Compact spaces are topological spaces where every open cover has a finite subcover, while Polish spaces are separable completely metrizable spaces. The key intersection is that every compact metric space is Polish because compactness implies completeness and separability under a metric. However, Polish spaces need not be compact, since they can be non-compact yet still separable and complete, illustrating a fundamental difference in their topological properties.
Applications in Mathematics and Beyond
Compact spaces are fundamental in topology, providing essential tools for continuity, convergence, and function analysis across various mathematical fields including analysis and differential geometry. Polish spaces, being separable completely metrizable spaces, enable rigorous treatment of measure theory, descriptive set theory, and probability, facilitating applications in stochastic processes and statistical mechanics. The interplay between compact and Polish spaces underpins modern approaches in functional analysis and dynamical systems, extending their impact to computer science, economics, and theoretical physics.
Conclusion: Choosing the Right Space for Analysis
Selecting between compact spaces and Polish spaces depends largely on the specific analytical requirements and desired topological properties. Compact spaces ensure every open cover has a finite subcover, making them ideal for problems requiring completeness and boundedness, while Polish spaces, being separable and completely metrizable, provide a robust framework for descriptive set theory and probability. Understanding the trade-offs in separability, metrizability, and compactness guides researchers in choosing the optimal space for advanced topological and functional analysis.
Compact space Infographic
 libterm.com
libterm.com