Computable refers to the ability of a problem or function to be solved or processed by a computational system, such as an algorithm or a machine. Understanding the concept of computability is essential for developing efficient software and algorithms that can handle complex tasks and data. Explore the rest of the article to discover how computable principles impact technology and problem-solving in everyday applications.
Table of Comparison
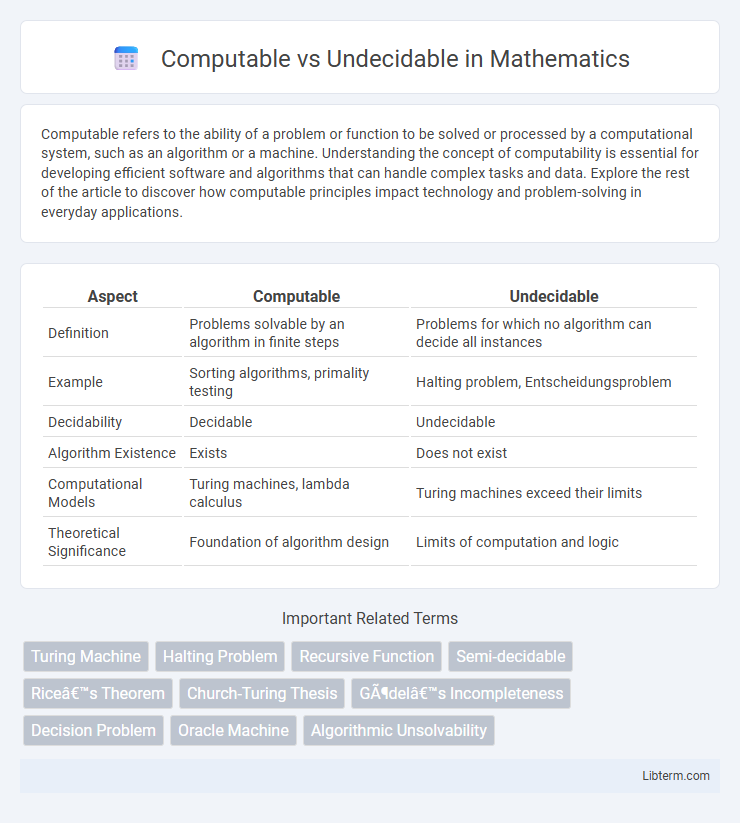
| Aspect | Computable | Undecidable |
|---|---|---|
| Definition | Problems solvable by an algorithm in finite steps | Problems for which no algorithm can decide all instances |
| Example | Sorting algorithms, primality testing | Halting problem, Entscheidungsproblem |
| Decidability | Decidable | Undecidable |
| Algorithm Existence | Exists | Does not exist |
| Computational Models | Turing machines, lambda calculus | Turing machines exceed their limits |
| Theoretical Significance | Foundation of algorithm design | Limits of computation and logic |
Introduction to Computability Theory
Computability theory explores which problems can be solved algorithmically, distinguishing between computable and undecidable problems. Computable problems have algorithms that produce solutions in finite steps, while undecidable problems lack any algorithm capable of providing answers for all inputs. The Halting Problem exemplifies undecidability, demonstrating fundamental limits of algorithmic computation.
Defining Computable Problems
Computable problems are those that can be solved by an algorithm within finite time, meaning there exists a step-by-step procedure to determine an answer for every input instance. These problems belong to the class of decision problems for which a Turing machine halts with a correct "yes" or "no" output. Defining computable problems helps distinguish them from undecidable problems, where no algorithm can guarantee a solution for all inputs.
Understanding Undecidable Problems
Undecidable problems are decision problems for which no algorithm can provide a solution for all possible inputs, meaning no computable function exists to decide the problem universally. The Halting Problem exemplifies undecidability by proving it is impossible to determine algorithmically whether any given program halts or runs indefinitely. Understanding undecidable problems highlights fundamental limits in computation and impacts areas such as logic, formal verification, and complexity theory.
Historical Background of Computability
The historical background of computability traces back to the early 20th century when mathematicians like Alan Turing and Alonzo Church formulated formal definitions of algorithms and computation, leading to the Church-Turing thesis. This thesis established the foundation for distinguishing computable problems, solvable by an algorithm, from undecidable problems, which no algorithm can resolve in all cases. The concept of undecidability emerged prominently with Turing's proof of the Halting Problem's undecidability, profoundly influencing theoretical computer science and the limits of computation.
Key Examples of Computable Functions
Computable functions include arithmetic operations like addition and multiplication, as well as algorithms for sorting and searching data efficiently. The factorial function and the greatest common divisor (GCD) computation are classic examples of functions that Turing machines can compute. These functions contrast with undecidable problems, such as the Halting Problem, which no algorithm can solve for all inputs.
Classic Cases of Undecidable Problems
Classic cases of undecidable problems include the Halting Problem, which determines whether a given program will halt or run indefinitely, and the Entscheidungsproblem, questioning the existence of an algorithm to decide the truth of logical statements. These problems illustrate the limits of computability, where no general algorithm can solve all instances within finite time. Rice's Theorem further generalizes undecidability by stating that all non-trivial semantic properties of programs are undecidable.
The Role of Turing Machines
Turing machines serve as the foundational model for computability, defining problems that can be algorithmically solved through finite procedures. Computable problems are those for which a Turing machine halts with a correct output on all valid inputs, while undecidable problems lack any Turing machine algorithm capable of providing a solution in all cases. This distinction highlights the limitations of algorithmic computation and the boundary between solvable and unsolvable decision problems in theoretical computer science.
Implications for Computer Science
Computable problems, solvable by algorithms within finite time, form the foundation of automated reasoning and software development, enabling efficient problem-solving across diverse domains. Undecidable problems, such as the Halting Problem, reveal inherent limits in algorithmic computation, challenging assumptions about what computers can achieve. Recognizing these limitations guides the design of programming languages, complexity theory, and formal verification methods, shaping realistic expectations for machine capabilities and prompting alternative approaches like approximation and heuristics.
Real-world Applications and Limitations
Computable problems, such as sorting algorithms and encryption, drive essential real-world applications by enabling reliable automation and security in technology systems. Undecidable problems, including the halting problem, expose inherent limits in computational theory, highlighting that certain questions cannot be resolved by any algorithm. These limitations impact fields like software verification and artificial intelligence, where guaranteeing absolute correctness or predictability remains impossible.
Future Directions in Computability Research
Future directions in computability research emphasize exploring the boundaries between computable and undecidable problems through advanced models like quantum computing and hypercomputation. Researchers aim to develop novel algorithms that can approximate solutions for traditionally undecidable problems, enhancing practical applications in artificial intelligence and cryptography. Investigating the interactions between complexity theory and computability paves the way for breakthroughs in understanding computational limits and expanding the scope of solvable problems.
Computable Infographic
 libterm.com
libterm.com