A flat surface provides a level and even area essential for various tasks, from construction to everyday use. It ensures stability and accuracy, making it ideal for placing objects or performing measurements. Discover more about the importance and applications of flat surfaces in different fields by reading the full article.
Table of Comparison
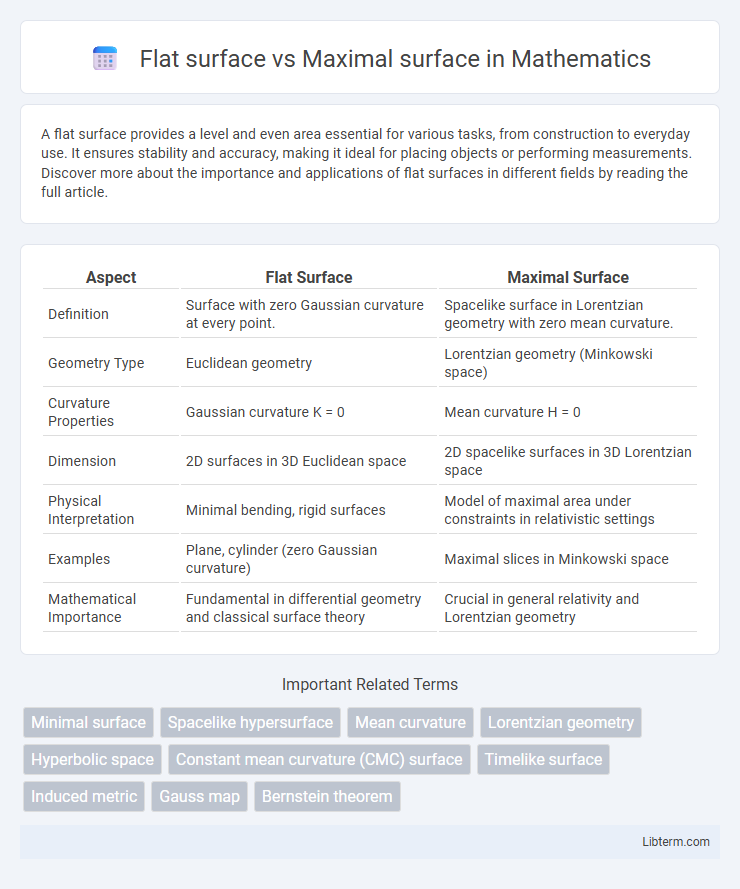
| Aspect | Flat Surface | Maximal Surface |
|---|---|---|
| Definition | Surface with zero Gaussian curvature at every point. | Spacelike surface in Lorentzian geometry with zero mean curvature. |
| Geometry Type | Euclidean geometry | Lorentzian geometry (Minkowski space) |
| Curvature Properties | Gaussian curvature K = 0 | Mean curvature H = 0 |
| Dimension | 2D surfaces in 3D Euclidean space | 2D spacelike surfaces in 3D Lorentzian space |
| Physical Interpretation | Minimal bending, rigid surfaces | Model of maximal area under constraints in relativistic settings |
| Examples | Plane, cylinder (zero Gaussian curvature) | Maximal slices in Minkowski space |
| Mathematical Importance | Fundamental in differential geometry and classical surface theory | Crucial in general relativity and Lorentzian geometry |
Introduction to Flat and Maximal Surfaces
Flat surfaces are characterized by zero Gaussian curvature, representing locally Euclidean geometry and often appearing in differential geometry and minimal surface theory. Maximal surfaces, prominent in Lorentzian geometry, are spacelike surfaces in Minkowski space with zero mean curvature, serving as analogs to minimal surfaces in Riemannian geometry. Both surfaces provide critical insights into curvature behavior and geometric analysis in their respective ambient spaces.
Mathematical Definitions
Flat surface in differential geometry is defined as a surface with zero Gaussian curvature at every point, implying that its intrinsic geometry is Euclidean and it can be locally isometrically mapped to a plane. Maximal surface refers to a spacelike surface in Lorentzian geometry that has zero mean curvature, serving as a critical point for the area functional in Minkowski space, analogous to minimal surfaces in Euclidean settings. The key mathematical difference is that flat surfaces focus on vanishing Gaussian curvature while maximal surfaces emphasize vanishing mean curvature under a Lorentzian metric.
Key Differences Between Flat and Maximal Surfaces
Flat surfaces are characterized by zero mean curvature, meaning they locally minimize area without bending, while maximal surfaces exist in Lorentzian geometry and possess zero mean curvature in a spacetime context, maximizing volume under specific constraints. The key difference lies in their ambient space: flat surfaces reside in Euclidean spaces, and maximal surfaces occur in Minkowski spaces where time-like dimensions influence their geometry. Flat surfaces reflect minimal energy configurations in classical geometry, whereas maximal surfaces relate to optimal spatial slices in general relativity and Lorentzian manifolds.
Geometric Properties
Flat surfaces exhibit zero Gaussian curvature, characterized by Euclidean geometry where parallel lines remain equidistant and angle sums in triangles equal 180 degrees. Maximal surfaces, found in Lorentzian geometry, possess zero mean curvature but can have varying Gaussian curvature, often appearing as spacelike hypersurfaces maximizing area locally in Minkowski space. The fundamental difference lies in curvature constraints: flat surfaces have uniform geometric properties with zero intrinsic curvature, whereas maximal surfaces balance mean curvature to optimize metrics in pseudo-Riemannian manifolds.
Applications in Mathematics and Physics
Flat surfaces in mathematics serve as fundamental models for Euclidean geometry with zero Gaussian curvature, facilitating the study of complex analysis, differential equations, and geometric structures. Maximal surfaces, characterized by zero mean curvature in Lorentzian geometry, are crucial in general relativity and the theory of spacelike hypersurfaces, modeling phenomena such as cosmic strings and spacetime singularities. Applications in physics leverage flat surfaces to analyze minimal energy configurations, while maximal surfaces help describe optimal causal hypersurfaces in spacetime manifolds.
Notable Examples of Flat Surfaces
Notable examples of flat surfaces include the Euclidean plane, which is a two-dimensional surface with zero curvature used extensively in classical geometry and engineering. The torus, when considered with a flat metric, also serves as a flat surface in differential geometry, providing insights into complex topology and string theory. Additionally, the Klein bottle represents a non-orientable flat surface embedded in four-dimensional space, relevant in advanced mathematical physics and topology.
Notable Examples of Maximal Surfaces
Maximal surfaces, characterized by zero mean curvature in Lorentzian geometry, include notable examples such as the Lorentzian catenoid and the Scherk surface, which exhibit unique geometric properties distinct from flat surfaces that have zero Gaussian curvature. The Lorentzian catenoid serves as a classic example where the surface is maximal but not flat, illustrating the differences in curvature behavior under Lorentzian metrics. Scherk-type maximal surfaces showcase complex configurations with periodicity and saddle points, providing important models in the study of differential geometry and general relativity.
Analytical Methods for Surface Comparison
Analytical methods for surface comparison between flat and maximal surfaces leverage differential geometry tools such as curvature analysis and conformal mapping to quantify geometric properties. Techniques like Gaussian curvature and mean curvature allow precise differentiation by identifying intrinsic and extrinsic curvature behaviors, enabling robust classification of surfaces as flat or maximal. Computational algorithms integrating partial differential equations and variational principles facilitate accurate surface fitting and curvature estimation, optimizing surface comparison in applications like material science and computer vision.
Challenges in Surface Classification
Challenges in surface classification arise from the intrinsic complexity of differentiating flat surfaces, characterized by zero Gaussian curvature, from maximal surfaces, which are spacelike surfaces with zero mean curvature in Lorentzian manifolds. Accurate identification demands advanced geometric analysis and computational methods to handle curvature variations and singularities that obscure clear boundaries. The interplay of local and global surface properties complicates algorithmic classification, necessitating robust modeling in differential geometry and computer vision applications.
Future Research Directions
Future research in flat surface and maximal surface studies aims to develop advanced computational models for accurately characterizing their geometric properties in higher-dimensional spaces. Investigations into the interplay between curvature constraints and topological variations will enhance applications in material science, particularly in optimizing structural stability and flexibility. Exploring quantum geometric effects on these surfaces may open new pathways in theoretical physics and complex system design.
Flat surface Infographic
 libterm.com
libterm.com