A subgroup is a smaller set contained within a larger group that satisfies the same operation rules as the entire group. Understanding the relationship between subgroups and groups is essential in fields like algebra and symmetry analysis. Explore the article to deepen your knowledge about how subgroups function within group theory.
Table of Comparison
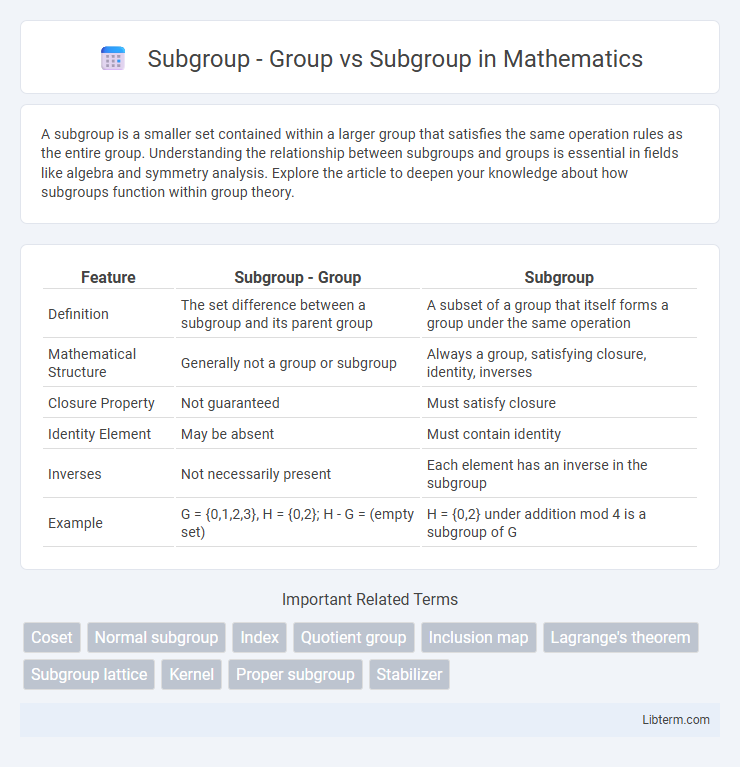
| Feature | Subgroup - Group | Subgroup |
|---|---|---|
| Definition | The set difference between a subgroup and its parent group | A subset of a group that itself forms a group under the same operation |
| Mathematical Structure | Generally not a group or subgroup | Always a group, satisfying closure, identity, inverses |
| Closure Property | Not guaranteed | Must satisfy closure |
| Identity Element | May be absent | Must contain identity |
| Inverses | Not necessarily present | Each element has an inverse in the subgroup |
| Example | G = {0,1,2,3}, H = {0,2}; H - G = (empty set) | H = {0,2} under addition mod 4 is a subgroup of G |
Introduction to Groups and Subgroups
Groups in abstract algebra are sets equipped with a binary operation satisfying closure, associativity, identity, and invertibility principles, forming the foundational structure in group theory. Subgroups are subsets of groups that themselves fulfill all group axioms under the same operation, serving as essential tools for understanding group composition and symmetry. Recognizing the relationship between groups and subgroups allows mathematicians to analyze complex algebraic systems by studying their smaller, more manageable components.
Defining Groups in Mathematics
A subgroup in mathematics is a subset of a group that itself satisfies the group axioms under the same operation, maintaining closure, associativity, identity, and invertibility. Groups are fundamental algebraic structures consisting of a set equipped with a single binary operation that combines any two elements to form a third element within the set. Defining groups involves specifying the operation and verifying the four key properties, while identifying a subgroup requires demonstrating that the subset inherits these properties from the larger group.
What Constitutes a Subgroup?
A subgroup is a subset of a group that itself forms a group under the same binary operation. To constitute a subgroup, the subset must satisfy three key criteria: closure under the group operation, existence of the identity element, and presence of inverses for each element within the subset. These properties ensure the subgroup maintains the algebraic structure inherent to the original group, enabling consistent internal operations.
Key Properties of Subgroups
Subgroups are subsets of a group that themselves satisfy the group axioms, including closure, associativity, the existence of an identity element, and inverses for every element. Key properties of subgroups include the fact that the identity element of the subgroup matches that of the parent group and that subgroups must be closed under the group operation and taking inverses. Every subgroup inherits the associativity of the parent group operation, ensuring the subgroup maintains a consistent algebraic structure within the larger group.
Criteria for Subgroup Identification
Subgroups are identified within groups based on specific criteria such as shared characteristics, behaviors, or predefined attributes that distinguish them from the larger parent group. Key factors include demographic variables like age, gender, and ethnicity, as well as clinical or behavioral markers relevant to research or analysis objectives. Precise subgroup identification enhances targeted interventions and improves the accuracy of data interpretation in studies and applications.
Group vs Subgroup: Core Differences
Groups are fundamental algebraic structures consisting of a set equipped with an operation that combines any two elements to form a third element, satisfying closure, associativity, identity, and invertibility. Subgroups are subsets of groups that themselves satisfy all group axioms under the same operation, meaning every subgroup is a group, but not every subset qualifies as one. The core difference lies in the subgroup's requirement to maintain group properties within the larger group, ensuring structural integrity and enabling further analysis of group behavior through its substructures.
Examples of Groups and Their Subgroups
A group is a mathematical structure consisting of a set combined with an operation that satisfies closure, associativity, identity, and invertibility, such as (Z, +), the integers under addition. A subgroup is a subset of a group that itself forms a group under the same operation, for example, the even integers form a subgroup of (Z, +). Other examples include the group of real numbers under multiplication (R\{0}, x) and its subgroup of positive real numbers (R^+, x).
Importance of Subgroups in Abstract Algebra
Subgroups are fundamental in abstract algebra as they provide a structured way to analyze the properties of larger groups by studying smaller, more manageable subsets that themselves satisfy group axioms. Understanding subgroups allows mathematicians to classify groups, explore homomorphisms, and investigate factor groups, which are essential for simplifying complex algebraic structures. The importance of subgroups lies in their role in revealing the internal symmetry and behavior of groups, facilitating deeper insights into group theory and its applications across mathematics.
Common Misconceptions: Group vs Subgroup
A subgroup is a subset of a group that itself satisfies the group axioms, including closure, associativity, identity, and inverses. A common misconception is assuming any subset of a group automatically forms a subgroup, ignoring the need for these structural properties. Another error involves confusing the smaller subgroup's identity element with different elements, while the subgroup must share the same identity as the parent group.
Applications of Groups and Subgroups
Groups provide a fundamental framework for algebraic structures used in various applications such as symmetry analysis, cryptography, and physics. Subgroups, as subsets that themselves satisfy group properties, enable the decomposition and study of groups by isolating smaller, more manageable components. This hierarchical structure assists in solving complex problems by examining invariant properties and simplifying computations within larger algebraic systems.
Subgroup - Group Infographic
 libterm.com
libterm.com