Holomorphic functions are complex functions that are differentiable at every point within their domain, exhibiting remarkable smoothness and analytic properties. These functions play a crucial role in complex analysis, enabling powerful techniques such as contour integration and conformal mapping. Explore the rest of the article to uncover the fascinating applications and deeper insights into holomorphic functions.
Table of Comparison
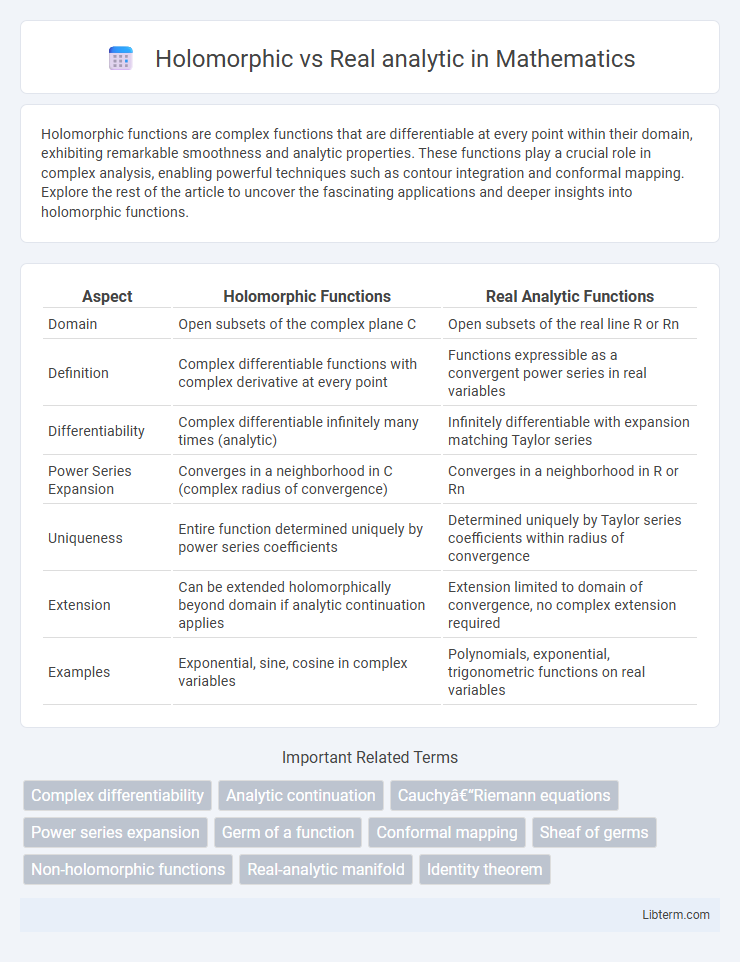
| Aspect | Holomorphic Functions | Real Analytic Functions |
|---|---|---|
| Domain | Open subsets of the complex plane C | Open subsets of the real line R or Rn |
| Definition | Complex differentiable functions with complex derivative at every point | Functions expressible as a convergent power series in real variables |
| Differentiability | Complex differentiable infinitely many times (analytic) | Infinitely differentiable with expansion matching Taylor series |
| Power Series Expansion | Converges in a neighborhood in C (complex radius of convergence) | Converges in a neighborhood in R or Rn |
| Uniqueness | Entire function determined uniquely by power series coefficients | Determined uniquely by Taylor series coefficients within radius of convergence |
| Extension | Can be extended holomorphically beyond domain if analytic continuation applies | Extension limited to domain of convergence, no complex extension required |
| Examples | Exponential, sine, cosine in complex variables | Polynomials, exponential, trigonometric functions on real variables |
Introduction to Holomorphic and Real Analytic Functions
Holomorphic functions are complex functions that are complex-differentiable at every point in an open subset of the complex plane, characterized by satisfying the Cauchy-Riemann equations and possessing power series expansions convergent within their radius of convergence. Real analytic functions, defined on real intervals, can be locally expressed as convergent power series with real coefficients, ensuring smoothness and infinite differentiability but without the strict complex differentiability conditions. The distinction lies in holomorphic functions requiring complex differentiability, yielding stronger regularity and rigidity properties compared to real analytic functions, which only require real-variable analyticity.
Fundamental Definitions: Holomorphic vs Real Analytic
Holomorphic functions are complex-valued functions defined on an open subset of the complex plane that are complex differentiable at every point, implying they satisfy the Cauchy-Riemann equations; this leads to infinitely differentiable and locally expressible as convergent power series in complex variables. Real analytic functions are defined on real domains and are infinitely differentiable functions whose Taylor series at any point converges to the function in a neighborhood of that point, ensuring local representability by convergent power series in real variables. The fundamental distinction lies in holomorphic functions being complex differentiable with stronger conditions and richer structures such as conformality, whereas real analytic functions require differentiability over real variables with series convergence but do not necessarily satisfy complex differentiability conditions.
Key Differences in Complex and Real Domains
Holomorphic functions are complex-differentiable in an open subset of the complex plane, exhibiting infinite differentiability and conformality, whereas real analytic functions are infinitely differentiable real-valued functions defined on real intervals with power series expansions converging locally. The Cauchy-Riemann equations characterize holomorphicity, linking partial derivatives of real and imaginary parts, a condition absent in real analytic functions that only require convergence of Taylor series. Holomorphic functions have stronger rigidity properties, such as uniqueness of analytic continuation, while real analytic functions can behave more flexibly across real domains without complex structure constraints.
Analyticity Criteria: Complex vs Real Analysis
Holomorphic functions in complex analysis satisfy stronger analyticity criteria than real analytic functions, requiring complex differentiability at every point in an open domain. While real analytic functions are defined by convergent power series in real variables, holomorphic functions possess complex differentiability characterized by the Cauchy-Riemann equations, ensuring infinite differentiability and conformality. This distinction highlights that holomorphicity implies real analyticity, but real analyticity does not guarantee holomorphicity due to the restrictive nature of complex differentiability.
Convergence of Power Series: Holomorphic and Real Analytic Functions
Holomorphic functions exhibit power series expansions with radius of convergence determined by the distance to the nearest singularity in the complex plane, ensuring uniform convergence within this radius. Real analytic functions also admit power series expansions centered at a point, converging to the function on some real interval; however, their convergence may be more limited due to the absence of complex-domain constraints. The interplay between complex analyticity and convergence domains highlights the stronger rigidity of holomorphic functions compared to real analytic functions.
Implications in Higher Dimensions
Holomorphic functions, defined over complex variables, exhibit stronger rigidity and stronger structural properties compared to real analytic functions, especially in higher dimensions. In several complex variables, holomorphic functions must satisfy the Cauchy-Riemann equations, leading to phenomena such as unique continuation and analytic continuation that are absent or weaker in real analytic settings. This difference impacts areas like complex geometry and partial differential equations, where holomorphic functions provide more powerful tools for solving boundary value problems and understanding geometric structures.
Examples Illustrating Holomorphic and Real Analytic Functions
Holomorphic functions, such as f(z) = z2 + 3z + 2, are complex functions differentiable in an open subset of the complex plane, displaying complex differentiability and conformality, exemplified by exponential functions like e^z. Real analytic functions, including f(x) = sin(x) or f(x) = e^x, are infinitely differentiable on real intervals with power series expansions converging to the function, as seen in the Taylor series expansions centered at real points. The function f(z) = |z|2 is real analytic on R2 but not holomorphic, highlighting the difference in differentiability requirements and domain between these function classes.
Relationship and Overlap Between the Two Concepts
Holomorphic functions, defined by complex differentiability, form a subset of real analytic functions, which are infinitely differentiable and equal to their Taylor series in real variables. The overlap occurs because every holomorphic function is inherently real analytic when restricted to real variables, ensuring smoothness and analyticity in both complex and real domains. However, real analytic functions may not extend holomorphically into the complex plane, highlighting the nuanced relationship between complex and real analyticity.
Applications in Mathematics and Physics
Holomorphic functions exhibit complex differentiability, making them essential in complex analysis, quantum field theory, and string theory due to their conformal invariance and analytic continuation properties. Real analytic functions, defined by convergent power series on real domains, are crucial in differential geometry and dynamical systems for modeling smooth real-world phenomena and solving differential equations. The distinction between holomorphic and real analytic functions underpins methods in mathematical physics, influencing solutions to problems involving complex manifolds and real variable boundary conditions.
Summary and Conclusion
Holomorphic functions are complex-differentiable and exhibit strong rigidity, allowing representation by convergent power series in a complex domain, while real analytic functions are defined by power series expansions on real domains without requiring complex differentiability. The complex structure imposes stricter conditions on holomorphic functions, leading to properties such as conformality and harmonicity that do not necessarily hold for real analytic functions. Understanding the distinction highlights the deeper regularity and geometric implications of holomorphicity, which are central in complex analysis and its applications.
Holomorphic Infographic
 libterm.com
libterm.com